CSU 1355 地雷清除计划

　　题目链接：http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1355

　　好题，根本想不到是网络流。

　　模型如图：

 

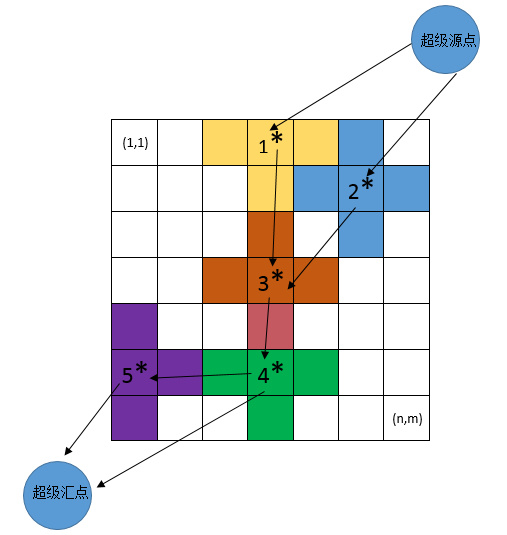
　　假想从右上角到左下角有一条阻拦线，我们就是需要把这条线剪短，搞出一个缺口，使得可以从(1,1)到(n,m)。这个与求网络流的最小割不谋而合，根据上面这个图建立网络流模型，对于a,b两个位置：

　　1. 如果a.x == b.x 或者 a.y ==  b.y，那么当|a - b| <= 2*k+1时，从ab之间连一条边（如上图1 -> 3）；

　　2. 如果a.x != b.x 并且 a.y != b.y，那么 当|a - b| <= 2*k+2时，从ab之间连一条边（如上图2 -> 3）；

　　3. 如果a节点覆盖到了上边或右边，那么从超级源点连边到a节点（如上图源点到1和2）；

　　4. 如果a节点覆盖到了下边或左边，那么从a节点连边到超级汇点（如上图4和5到汇点）；

　　当然，必须对每个点进行拆点，这个就不多讲了。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define L(u) ((u) << 1)
#define R(u) ((u) << 1 | 1)
#define N 1005
#define M 200005
#define INF 0x3f3f3f3f

int gap[N],dis[N],pre[N],cur[N];
int n, m, k, NE, s, t;
int head[N];
char g[55][55];

struct Node{
    int c,pos,next;
}E[M];

struct Mine
{
    int x, y;
    int id;
}mine[205];

inline void checkmin(int &a,int b)  {if(a == -1 || a > b)a = b;}

void add_edge(int u,int v,int c)
{
    E[NE].c = c;
    E[NE].pos = v;
    E[NE].next = head[u];   
    head[u] = NE++;
    
    E[NE].c = 0;    // !反向初始为0
    E[NE].pos = u;
    E[NE].next = head[v];   
    head[v] = NE++;
}

int sap()
{
    memset(dis,0,sizeof dis);
    memset(gap,0,sizeof gap);
    memcpy (cur, head, sizeof dis);
    int u=pre[s]=s,maxflow=0,aug=-1;
    gap[0]=n;
    while(dis[s]<n)
    {
loop:for(int &i=cur[u];i!=-1;i=E[i].next)
        {
            int v=E[i].pos;
            if(E[i].c && dis[u]==dis[v]+1)
            {
                checkmin(aug, E[i].c);
                pre[v]=u;
                u=v;
                if(v==t)
                {
                    maxflow+=aug;
                    for(u=pre[u];v!=s;v=u,u=pre[u])
                    {
                        E[cur[u]].c-=aug;
                        E[cur[u]^1].c+=aug;
                    }
                    aug=-1;
                }
                goto loop;
            }
        }
        int mindis=n;
        for(int i=head[u];i!=-1;i=E[i].next)
        {
            int v=E[i].pos;
            if(E[i].c && mindis>dis[v])
            {
                cur[u]=i;
                mindis=dis[v];
            }
        }
        if((--gap[dis[u]])==0) break;
        gap[dis[u]=mindis+1]++;
        u=pre[u];
    }
    return maxflow;
}
 
void init()
{
    memset(head, -1, sizeof head);
    NE = 0;
}
 
int main()
{
    int cas;
    scanf("%d", &cas);
    while(cas--)
    {
        scanf("%d%d%d", &n, &m, &k);
        init();
        
        int id = 1;
        for(int i = 0; i < n; i++)
        {
            scanf("%s", g[i]);
            for(int j = 0; j < m; j++)
                if(g[i][j] == '*')
                {
                    mine[id].x = j;
                    mine[id].y = i;
                    mine[id].id = id++;
                }
        }
        s = 0, t = L(id);
        
        for(int i = 1; i < id; i++)
        {
            Mine a = mine[i];
            if(a.y - k <= 0 || a.x + k >= m-1)
                add_edge(s, L(i), INF);
                
            if(a.y + k >= n-1 || a.x - k <= 0)
                add_edge(R(i), t, INF);
            
            for(int j = i; j < id; j++)
            {
                if(i == j)
                    add_edge(L(i), R(i), 1);
                else
                {
                    Mine b = mine[j];
                    if(((a.x == b.x) && (abs(a.y-b.y) <= 2*k+1)) || 
                       ((a.y == b.y) && (abs(a.x-b.x) <= 2*k+1)))
                       {
                           add_edge(R(i), L(j), INF);
                           add_edge(R(j), L(i), INF);
                       }
                        
                    else if((a.x != b.x && a.y != b.y) && abs(a.x-b.x) + abs(a.y-b.y) <= 2*k+2)
                    {
                        add_edge(R(i), L(j), INF);
                        add_edge(R(j), L(i), INF);
                    }
                        
                } 
            }
        }
        
        n = (id-1) * 2 + 2; // 所构造图的总节点数
        int res=sap();
        printf("%d\n", res);
    }
    return 0;
}