Atcoder总结 Part II
ARC70E NarrowRectangles
以后做题的时候,如果看出来DP,至少先把想到的式子先写出来,不要停留在脑中思考,并且做题时候不要固化思维,看出来一些性质时候,但没有进展的时候,不要死磕这种方法,要跳出来,重新看问题
首先看出300分部分是一个DP,设$dp[i][j]$为前$i$个矩形且第$i$个矩形左端点在$j$的最小代价
那么$dp[i][j]=\min\limits_{k \in[j-len_{i-1}+1,j+len_i-1]}dp[i-1][k]+|j-l_i|$
那么就可以得到300分
然后考虑将$dp[i]$看作一个关于j的函数,其实通过观察可以发现,最终$dp[i]$的函数就是由若干个绝对值函数相加得到的,那么对于这种函数,是一个下凸包,并且存在$[-i-1,i+1]$斜率的函数
首先关注最简单的情形$i=1$时,$dp[1]=|j-l_1|$,就是一个绝对值函数
将情况扩展,当前的函数由两部分组成,$dp[i-1]$在某一段区间的最小值,$|j-l_i|$,首先看$dp[i]$这一部分的贡献,这个区间取$min$操作相当于是把这个函数从斜率为$0$的部分劈开,各自向左向右平移得到
形式化的,对于函数斜率为$0$的分界点$a_{i-1},b_{i-1},a_i=a_{i-1}-(len_i-1),b_i=b_{i-1}+(len_{i-1}-1)$
然后考虑$y=|j-l_i|$,对于原来函数在$l_i$左边的图像,所有线的斜率$-1$,对于在$l_i$右边的图像,所有线的斜率$+1$
通过上面性质的分析,那么可以用两个堆来维护这些斜率的分界点,每一次扩展的时候,讨论$l_i$的位置,然后维护一下,斜率为$0$的取值,最终答案就是$dp[n]$斜率为$0$部分的取值
ARC70F HonestOrUnkind
如果之前了解过摩尔投票法,这道题也许就可以想出来
首先可以看出来如果$A\leq B$那$Impossible$,因为$unkind$的人都可以模仿对应的$honest$,那么你就无法分辨
我们目标就是在$n$次询问下,找到一个$honest$,然后再用$n$次询问判断其他人
首先如果一个人$a$,问他$b$是否是$honest$,如果得到的回答是$NO$,那么说明$a,b$中至少有一个人是$Unkind$的,如果把这两个人删去,$A$仍然大于$B$
由于在$n$个人中,$A>B$,$honest$占了大多数,那么利用摩尔投票法的思想,维护一个栈,依次检查$n$个人,每一次用栈顶的人问当前这个人,如果回答为$NO$,那么弹出,否则压入栈
由于最终栈里面至少有一个$honest$,并且每一个栈的元素对于下一个元素的回答都是$Yes$,那么那些$Unkind$的人,一定连续地在栈底,那么栈顶元素一定为$honest$
ARC68F Solitaire
好难……
可以发现,双端队列中的元素,以$1$为分界点左右两端都是一个递减的序列
然后得到的$1$到$k-1$的序列,是一段全部选完,然后另一端选出一部分
剩下的位置由于剩下的可以随便从剩余的双端队列两端选,每一个位置有$2$种选择,直到只剩$1$个数,那么方案即为$2^{n-k-1}$
由于原来的都是递减序列,那么得到的合法序列一定可以分解成两个递减的序列,并且其中没有选完的序列的最小值是大于没有选在$1$到$k-1$的序列中的最大值
那么一个序列是要去满足这个条件,由于这个序列是需要从后往前连续选的,如果不这样选,那么会存在一个元素,使得两个序列最终的最小值都比这个数小,那么不符合条件
记$dp[i][j]$表示填到前$i$个位置,其中一个序列的最小值为$j$的方案数,并且需要保证另外一个序列的当前最小值是$>j$,这样才能保证,得到的方案是唯一的(一个序列可以唯一地分解为两个递减序列并保证其中一个序列在每一个原来序列的当前最小值都小于另一个序列的当前最小值)
由于一个序列需要从后往前填,那么$j-1>n-i$,即$j>n-i+1$
$dp[i][j]=\sum_{k>j}dp[i-1][k]+[j<n-i+2]dp[i-1][j]$
AGC11D Piling Up
之前做过一道题用了这道题的思想,对于这种一种状态会被多次算到的题目,可以考虑把所有的情况归到一种情况,其他的都不算,那么这样就可以只算一次,像这道题就是在一个区间内$[l,r]$都会被算到,不要去考虑具体算出来这个区间被算到了几遍,要关注的是如果到达某一个特定点时,才会统计答案,而这个特定点是只会被经过一次的状态,这道题就是$1$的个数变为$0$,相当于就是取到$[l,r]$的$l$时
记当前盒中的$1$的个数为$a$,$0$的个数为$b$,由于操作过后盒子中球的总和不变都是$n$,那么$a+b=n$
对于一次操作拿出的球是$00$,条件$a>0$,操作之后$a-1,b+1$
$11$,条件$b>0$,操作过后$a+1,b-1$
$01$,条件$a>0$,操作过后$a,b$
$10$,条件$b>0$,操作过后$a,b$
考虑设$dp[i][j]$表示前$i$个元素,当前盒中$1$的元素个数为$j$个
若$j>0$,$dp[i][j]\rightarrow dp[i+1][j],dp[i][j]\rightarrow dp[i+1][j-1]$
若$j<n$,$dp[i][j]\rightarrow dp[i+1][j],dp[i][j]\rightarrow dp[i+1][j+1]$
但是这样会算重,但是可以发现,一个状态可行的初始状态$1$的个数是一个区间,这是由于在填的过程中有对$1$个数的最小值的限制,也有对$0$的限制,对$0$的限制就是对$1$最大值的限制,所以一定合法的是一个区间
那么如果只在区间的左端点计算一次,那么就是只算过了一遍
那么相当于在操作的过程中$1$的个数达到过$0$个
那么$dp$多记一维即可
AGC20E Encoding Subsets
tourist永远的神
考虑设$dp[s]$表示字符串为$s$的答案
如果第一位填的是单个字母,那么$dp[s]=dp[s_{2..n}]*(1+s[0])$
如果填的是一个连续的重复段,考虑枚举这个连续段的长度i和循环的长度j,那么首先$j\mid i$,然后考虑在$s$子集中可以形成连续段的长度$i$和循环的长度$j$的字符串长什么样,先不去考虑$i$之后的元素(因为在后面DP时候会算到),那么可以发现,这个循环节就是$0$到$i-1$所有长度为$j$循环的字符串的“&”和,记作$t$,那么就变成了$t$的子问题(因为$t$所有子集形成的$s$前缀,$s$的子集也都能形成)方案数$f(t)$,转移$dp[s]=\sum \limits_t dp[t]*dp[s_{i...n}]$
综合上面两个转移即可算出答案,我在想的时候,用区间DP推到这里了,但是看到有新的字符串会产生,就以为这是个$O(2^n)$的DP,看完题解才发现naive
考虑在算循环节的时候,如果枚举的$j=i$,那么$dp[t]$是原来字符串的一个区间,那么这样的$t$最多有$O(n^2)$个,如果$j\neq 1$,那么$j \leq \frac{i}{2}$,而$t$的长度为$j$,那么说明每一次t的长度至少减半,最多进行$log$次转移
这就提示围我们,把较小的所有字符串先计算好$dp$值,然后记忆化搜索转移$DP$,处理到$13$是可以通过的
理论复杂度$O(n^3+n^2 2^{13})$,跑不满
AGC22E Median Replace
又是一种神奇的DP
首先先把可以得到1的所有的$3$个数字写出来,$0$的也是一样,会发现如果把其中的$0/1$抵消掉 ,那么最终决定得到的是什么是剩下的数字($000/111$除外)
再考虑如何贪心的判断一个确定字符串是否合法,可以发现我们需要贪心的减少$0$的数量,剩下不能消掉的$0$由$1$去抵消掉,如果$1$不够那么这个字符串不合法,否则就是合法,再进一步考虑如果当前消着消着,发现当前的字符串开头有至少$2$个$1$,那么这个字符串一定是合法,因为最后那个消出来的字符无论是$0$还是$1$,一定最后得到还是$1$
一开始我只想到把$0$给贪心搞掉,发现没有发现$2$个$1$的性质,思考的方向对的,但是还需要发现更多性质
那么我们限制考虑一位一位往后面消,并记录当前前面消成的字符串是怎么样的,由上面的性质得到,当前$1$的个数最大$2$个,$0$的个数也是最大$2$个,那么状态数只有$8$个,那么我们只要得到每一个状态之间的转移关系,那么我们就可以在建立出的转移关系图上DP,这张图是一个自动机
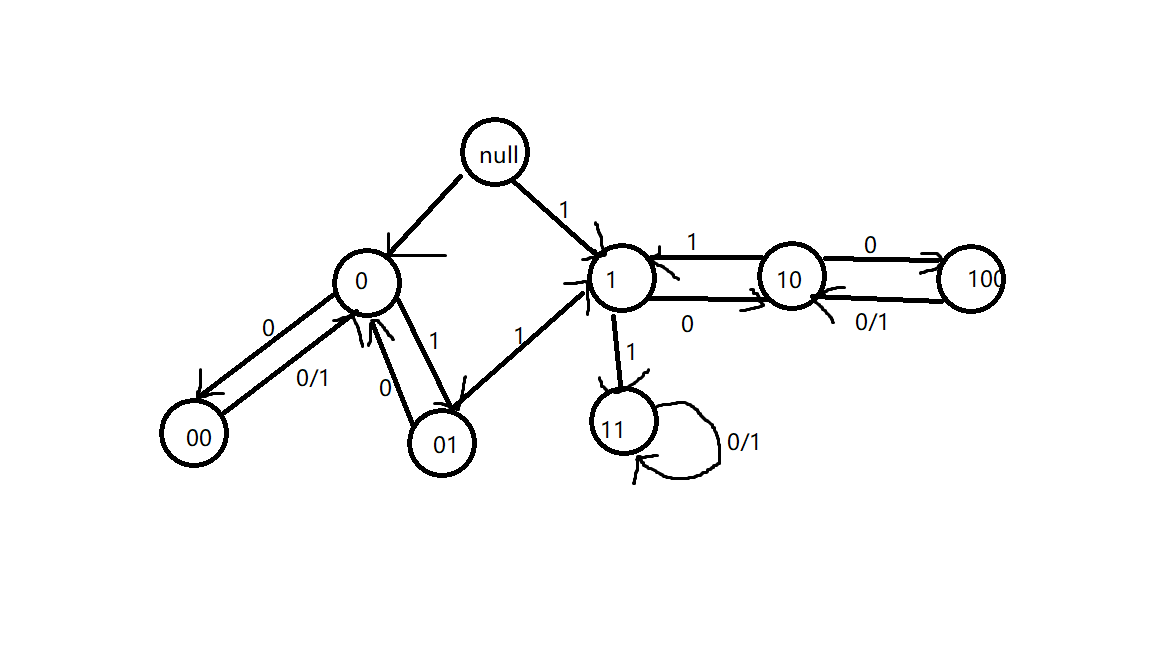
其中$11$是特殊的,由于如果到达了$11$,那么说明字符串一定合法,那么只要最终一直待在$11$处即可
其实最终的优化主要就是在$11$这个地方
最终答案为$1$和$11$处的dp值
AGC21E Ball Eat Chameleons
考虑最简单可以使一个变色龙变成红色的方案,就是$RB$
设$a$为$R$数量,$b$为$B$的数量
那么如果$a\geq b+n$,那么所有方案都可行
如果$b<a<b+n$,那么有$n-(a-b)$个是吃$RB$的,剩下的$a-b$个,先吞蓝,最终吞红,转化为前缀$B-R$的个数不大于$a-n$
如果$b=a$,最后一个一定为$B$,去掉变成子问题即可
类似卡特兰数一样折线法计数
AGC3E Candy Piles
一道模型转化题,利用了网格图的模型(这东西应用很广泛啊),这场F也是一道模型转化
考虑将$a_i$降序排序,并将$a_i$作为$i$位置上网格的节点的个数,那么可以画出一个网格图
考虑操作对应着什么,对于将最大值去掉的操作,对应着网格图上将最左边的一列去掉
将每一个非空的堆里拿走一个球对应着,将网格图上最下面一行删掉
这可以等价为一个点从网格的左下角出发,不断向上向右走,直到走到上轮廓为止,最后走到外面去的人输
那么可以发现对于图上的一个突起走到这个点一定是先手必败,那么由这些突起可以推出整一个图上每一个点的胜负情况
并且可以注意到一个性质,对于上轮廓上为$0$(必败)的点,从这点斜向下的斜线上的点都是$0$($1$也是一样),那么只要看左下点对应着上轮廓上的点的情况就可以确定答案了
上轮廓的点很好计算,多画图即可。这道题主要是模型转化的过程想不到
AGC37D Sorting a Grid
这种跟排列,每个位置只能选一次的限制,要想到二分图匹配的模型
对于题意,可以发现只要在第一次操作中,使得同一列中没有两个数最终的位置是在同一行的情况
主要是考虑如何构造出这组解,可以发现,如果只有一列这是二分图匹配的模型,只要对于每一行都建出一个节点,对于最终行建出节点,如果现在的行$i$上有最终行为$j$的元素,那么$i$向$j$连一条边,做二分图匹配即可,如果存在完美匹配那么一定存在方案
对于多个列那么就做多次二分图匹配,由于建出来的二分图是正则图,根据Hall定理,那么一定存在完美匹配,将这组完美匹配去掉之后,原图任然是一个正则图,那么做$m$次匹配即可
二分图匹配可以用网络流来做
AGC6DEF
AGC5DEF
AGC28D Chords
这种题可以先考虑不加限制的一些性质再去做
考虑一个联通块点集合中下标的最小值和最大值,那么在最小值和最大值之间的点不能向外面连边
那么考虑设$dp[i][j]$表示$i,j$在同一个联通块时并且分别为最小最大值的方案数,之后统计连通块数量之和用$dp$统计就很好统计
首先需要判断这个区间内有没有连向外面的边,如果有这个状态不合法
考虑统计出随便连边的方案数,再减去联通块端点不在$j$的方案,一开始转化成卡特兰数搞,会算重,很难统计,其实这时候考虑容斥是一个好的选择
对于一个$n$个点的环,随便连边的方案数为$f(n)=(n-1)(n-3)...3*1$,因为考虑先选出一个点,这个点可以连出$n-1$条不同的边,剩下的$n-2$个点继续随便连
那么$dp$转移式为
$dp[i][j]=f(cnt(i,j))-\sum\limits_{k=i+1}^{j-1} dp[i][k]f(cnt(k+1,j))$
最后统计答案即可,就是区间外的点随便连乘上这个区间的方案数,就是这个联通块的贡献
AGC33D Complexity
DP好题
首先可以发现答案的上界不会很大,是$logn+logm$级别的,因为可以不断从中间切开,直到只剩一个字母,而一个字母的复杂度是$0$
那么考虑枚举答案$ans$,问题就变成如何判定在操作$ans$次下是否可行,即把矩阵切成若干个复杂度为$0$的区域
但是这样直接推是$O(n^5)$的,这样没有利用之前计算的信息
现在设$dp[i][l][r][p]$表示在第$i$行,从$l$列到$r$列,用$p$次操作最多可以向下延伸多长距离,其实这一步就是把$0/1$状态压缩一下,将一个维度压缩成DP值
那么转移就显然了
$dp[i][l][r][p]=\min\limits_{k=l}^{r-1} \max(dp[i][l][k][p-1],dp[i][k+1][r][p-1])$
设$j=i+dp[i][l][r][p-1]$
$dp[i][l][r][p]=dp[i][l][r][p-1]+dp[j][l][r][p-1]$
时间复杂度$O(n^4logn)$,其中第一个转移可以通过决策的单调性优化到$O(n^3logn)$
AGC35D Add and Remove
很妙的DP
考虑将操作倒推,就是把数一个一个插入到相应的位置上,然后统计其贡献,我这都没有想到。。。这样就会清晰很多
首先两端的元素,最终只会算到答案中一次,那么他们的系数就是$x=1$
考虑将一个数插入到$i$和$i+1$中,由于删这个数的时候,会加到左右两边的数,那么这个数就会被算$x_i+x_{i+1}$次
那么可以设$dp[l][r][x][y]$表示原来数组里第$l$和第$r$个元素靠在一起,并且$l$的系数为$x$,$r$的系数为$y$,考虑枚举向中间插入了哪个数,计算贡献即可
复杂度看上去是$O(n^32^n)$,但好像不加记忆化都跑得飞快
AGC34E Complete Compress
首先可以考虑枚举每一个点作为集结点,如果所有$1$点到这个点的距离之和为偶数,那么就有可能可以在这个点集合
可以把问题转化为有$n$堆数(每一个堆是一个子树),每一次从两堆中选出一对数,让他们抵消掉,并且子树内也可以抵消
考虑没有子树内抵消的情况,设总和为$sum$,所有堆中最大值为$MAX$
若$sum-MAX\geq MAX$,那么一定可以用其他的堆来把最大堆抵消完,然后其他堆可以互相抵消掉,可以抵消掉$\left \lfloor \frac{n}{2} \right \rfloor$对
若$sum-MAX<MAX$,那么其他堆不能把最大堆抵消掉,最多抵消掉$\left \lfloor \frac{2MAX-sum}{2} \right \rfloor$对
由于堆内还可以抵消,这就变成一个子问题,利用树形DP递归下去
设$dp[x]$表示$x$的子树内最多可以抵消掉多少对,$sum[x]$表示所有$x$子树内的$1$点,到$x$距离之和,$MAX[x]$表示$x$的儿子子树内距离之和的最大值,$u$表示这个最大儿子
根据上面的讨论
如果是第一种情况,那么已经达到能抵消对数的上界,那么$dp[x]=\left \lfloor \frac{sum[x]}{2} \right \rfloor$
如果是第二种情况,那么首先可以消掉$sum[x]-MAX[x]$对,然后最大堆中剩下了$2MAX[x]-sum[x]$对,由于之前已经处理出来$u$子树内可以抵消掉多少对,那么还可以抵消掉$\left \lfloor \frac{\min(2MAX[x]-sum[x],2dp[u])}{2} \right \rfloor$,那么两个求和即可
这道题就是要把这个递归的子问题分析清楚,否则只停留在某一层分析,没有递归下去,这样会导致很多的假做法,由于树的递归性质,可以往这方面多想想
ARC106E Medals
许多知识的结合
首先考虑二分答案,对于每一个人可以把这个人拆成$k$个点,然后以人和天作为一张二分图的两部分端点,然后根据题意进行连边,如果这张二分图存在完美匹配,那么这个时间就是可行的
根据$Hall$定理,只要人那边任意一个点集的子集$S$,这个子集在天那边的相邻的节点集合记作$NS$,$|S|\geq |NS|$
由于$n$很小,那么考虑枚举所有$n$的集合,那么现在需要计算的就是对于一个人的集合,其可以选的天有多少个
考虑预处理出对于每一天,可以选这天的人的集合$p[i]$
对于某一个人集合$s$,可以选天就是$p[i]\&s\neq 0$,考虑补集转化,统计所有$p[i]\&s=0$,也就是$p[i] | \overline{s}=\overline{s}$
直接$fwt$处理即可
所以这道题套了图论,$Hall$定理,$FWT$,二分等诸多知识


