ATcoder Grand Contest总结
最前面:
AT的题都很有思维难度,总结一下一些AT的常规操作
1.对于有操作的题目,如果正面推不行的话考虑倒推,将操作转化,寻找更好的性质
2.模型转化,看到某一种的计算的式子,需要考虑有没有更简化的模型可以达到相同的效果
3.补集转化,正难则反
4.分析题目性质,计数题要找到一些限制条件或者构造方案使得计数不重不漏
目标:稳定三题
比例:D:0/1 C:3/6 B:2/3
10.12 - 10.22
AGC47:Solved A,B,C,D Aim E
AGC46:Solved A,B,C,D
AGC45:Solved C Aim B
AGC44:Solved A,B,C Aim D
AGC43:Solved A,B,D Aim C
AGC41:Solved B Aim D
AGC40:Solved C
AGC37C Numbers on a Circle
首先AT常规操作,考虑倒推。那么现在题目就变为
1.选择一个下标i,将$b_{i}$减去左右两边的数
2.题目的目标变为从$b$数组变为$a$数组
由于$a,b$都是正整数,在任意一次操作之后,不能使$b$中的数变为负数,那么$b_{i}>b_{i-1}+b_{i+1}$,然后由于$b$中的值只会减小不会增加,所以$b_{i}>a_{i}$
现在考虑如果i满足上述条件,那么$b_{i}>b_{i-1},b_{i}>b_{i+1}$,对于$i-1,i+1$上述条件一定不满足(第一个条件),所以必须先对i进行操作,才能对左右两个下标进行操作,那么其实操作的大体顺序已经定下来了。相当于每三个分一个组,先把满足条件的数放到队列里,对其进行操作之后再判断一下旁边的两个数是否可以进行操作,如果可以就将点加入队列中。
看到官方题解和网上很多题解都是将所有的数都扔到一个堆里每次取出最大的数进行操作,其实并不需要这个堆,因为中间那个数不进行操作的话,左右两边的数一定不会满足条件,其实每一轮操作的顺序都是环上每隔三个数有一个数进行操作,由于每个数互不影响,所以操作顺序不会影响操作数量
复杂度$O(nlogMAX)$
AGC37B RGB Balls
首先要考虑如何构造出一组最优的合法方案。考虑将每种球分组后以下标排序,然后将相同下标的三种球放在一起进行考虑
$a_1<a_2<a_3<...<a_{n-1}<a_n$
$b_1<b_2<b_3<...<b_{n-1}<b_n$
$c_1<c_2<c_3<...<c_{n-1}<c_n$
也就是将三种球的下标记录在$a$,$b$,$c$三个数组中,最终最优方案的答案就是$\sum_{i=1}^{n} max\{a_i,b_i,c_i\}-min\{a_i,b_i,c_i\}$
记$A$为$max\{a_i,b_i,c_i\}$组成的集合,$C$为$min\{a_i,b_i,c_i\}$,$B$为除$A,C$集合中其他的位置
可以发现$A$中所有元素都是对计算的值产生正的贡献,$C$中所有元素都是对计算的值产生负的贡献,$B$对计算的值无贡献
那么只要使最终的分配方案能使产生贡献的球都是$A,C$集合中的值即可
那么对于一个人,只要满足选到的球先是$C$集合中的,再是$B$集合中的,最后是$A$集合中的
从左往右枚举球,中途记录一下当前该选哪个集合的人有多少个,每次对答案乘上人数即可
AGC39C Division by Two with Something
首先要将题目转化一下,对于一个二进制数,对其进行操作就是将最后一位取反放到前面,然后删掉最后一位
可以将这个二进制下的数取反复制到原数的前面,那么一个循环中的数可以通过截取所有得到的新数中长度为$n$的子串得到
考虑一个循环是怎么形成的,一个数通过$2n$次操作一定会变回原来的数,相当于前$n$次操作对原来的数进行了取反,后面$n$次操作对已经取反的数再进行一次取反,两次取反就会得到原来的串
再考虑循环在字符串上的意义,一个最短的循环就是拼接起来得到的那个字符串的最小循环节长度
设循环的次数为i,因为通过$2n$次操作一定回到原数,$n$次操作得到取反后的串,那么$i\mid 2n$,$i\nmid n$
循环节内部是有一个串和它的反串拼起来的
枚举$2n$的因子$i$,统计对于存在循环节为i的串的个数,注意是循环节不是最小循环节(最后容斥回去即可)
如果前$i/2$位比$x$的前$i/2$位小,那么之后循环的时候一定在$x$以内
那么只要判断一下前$i/2$位等于$x$的前$i/2$位,然后构造出前$n$个,比较与$x$的大小,如果比$x$小就对统计的个数$+1$即可
但不过此时统计的数量并不是最小循环节的数量,一个循环节会在循环节长度的倍数处重复统计,最后枚举其倍数容斥即可
AGC36C GP 2
窝连最开始的限制条件都没想到
考虑最终的序列要满足什么条件才能被表示出来。很明显有$\sum_{i=1}^{n} x[i]=3m$,然后考虑一个数最大只能是$m$个$2$加起来,那么$\max_{i} x[i]\leqslant 2m$,由于是一个$+1$另一个$+2$,那么每一次最多改变一个数的奇偶性,那么$\sum_{i=1}^{n} [x[i]\%2=1]\leqslant m$
可以发现操作集合到满足这个限制条件序列的集合是一个满射,这种统计方案不重不漏
只考虑第一个和第三个限制条件,不考虑第二个,那么可以先在序列上若干个$1$,然后再在序列上放$2$,那么可以枚举放1的数量
$\sum_{i=0,(3m-i)\%2=0}^{m}C_{n}^{i}C_{n+\frac{3m-i}{2}-1}^{n-1}$
再考虑第二个限制条件,可以发现如果第二条件不满足,那么只有$1$个数不满足限制,那么考虑补集转化
枚举那个不满足的数有多大,再将剩下的数分配到$n-1$个位置里
再考虑一下第三个限制条件,可以发现,如果一个数大于$2m$,那么序列上不为$0$的数最多有$m$个数,即使全部都为奇数,也符合第三个限制条件,所以不用再考虑第三个限制条件
$n\sum_{i=2m+1}^{3m}C_{n+3m-i-2}^{n-2}$
两式相减即为答案
AGC34C Tests
可以发现,如果一门考试比另外一个人高了,那么重要度一定要设为$u_i$,并且要学到满分,因为每一门考试都有一个$b_i$,只有超过$b_i$才能反超另外一个人,那么有一门考试已经超过$b_i$,那就要充分利用这门考试,去学其他的考试一定没有比把这个考试学到满分优(因为还要先学到$b_i$才可以);如果一门考试比另外一个人低,那么重要度一定要设为$l_i$
那么在这种策略之下,最多只有一门考试学习过但没有学到满分,其他的考试要么没有学要么已经学到了满分,原因是可能有边角料的存在,会使得有一门课不是满分
因为一开始每一门考试都是$0$分,那么与另一个人的差距就是$tot=\sum_{i=1}^{n} b_il_i$,如果把第i门课学到满分可以缩小的差距就是$v_i=(x-b_i)u_i+b_il_i$,那么以$v$从大到小排序,贪心的选择能缩小差距最大的那门考试,将初始的差距减去$v_i$
那么就是以$v$从大到小排序之后,找到最大的$k$,使得$\sum_{i=1}^{n}v_i\leqslant tot$
但是因为不一定能把初始差距减到$0$,那么就需要有一门考试来处理这个边角料,考虑枚举这个考试,分两种情况讨论
如果当前枚举的考试在前$k$个中,那么将当前枚举到考试替换成第$k+1$个考试满分,然后判断计算当前这个考试需要的时间
如果不在,直接计算即可
考虑如何计算一个考试需要花费的时间,如果边角料少于$b_il_i$那么重要度设为$l_i$,否则就设为$u_i$
我看到网上和官方题解都是带了一个二分时间,其实并不需要
还有我一开始写的程序被corner case卡WA了,需要特判所有$b_i$都是$x$的情况
AGC47C Product Modulo
这种题AT很少见啊
看到这个式子会发现一般的处理方法很难进行处理,我比赛的时候打了一个整除分块,时间复杂度也假了。但可以发现这个模数给的很特殊,不是一般的$998244353$和$1e9+7$,那么从质数的性质出发
可以发现如果式子里不是乘法而是加法,那么是很好计算的,可以使用FFT或者其他的技巧计算,考虑如何把乘法变换为加法,很明显对乘数取一个$log$就可以化乘为加,那么考虑底数的选取
质数的原根$g$,保证在$1\leq i< p-1$,$g^{i}$两两不同,那么考虑用$g$作为底数,由于$p$不大,直接枚举次数,将每一个数取对数,然后用FFT加速加法运算(在每个数对应次数的位置$+1$,将这个多项式自乘$1$次)
AGC47D Twin Binary Trees
一个由i,j两个叶子节点组成的简单环是i到j在树上的路径和p[i]到p[j]树上的路径组合起来的,如果记录一下每一个叶子节点到根路径上节点标号的乘积$fac$,那么i到j的路径上的节点标号乘积就是$\frac{fac_ifac_j}{LCAfac[father_{LCA}]}$
考虑枚举每一个LCA,分别来自每一个节点左右子树的叶子节点组成的路径的LCA是当前节点,那么在第一棵树上的乘积很好计算,直接枚举左右子树的叶子节点。对于第二棵树,考虑先遍历左子树,对于叶子节点$i$,在$p[i]$到根节点的路径上每一个节点都打上标记,标记上记录通过这个点的所有路径的乘积之和,这里的乘积要乘上第一棵树的贡献,枚举右子树的所有叶子节点,也在第二棵树的上遍历,遍历到的点记录的权值减掉上一次遍历到的点乘上当前标号,就是左子树的叶子节点和这个节点LCA的乘积之和,累计答案即可
AGC24D Isomorphism Freak
首先需要发现如果要将两棵子树变成同构的话,所需要的最小的颜色数是两个子树深度的较大值,并且最小的叶子节点数就是每一层节点儿子数的最大值的乘积(因为要保证每一层都相同,而又不能删去节点,那么只能把这一层所有的节点的儿子都加到最大值,最后每一层乘起来就是叶子节点数)
那么考虑树的直径,当根定在树直径的中点时,所有子树深度的最大值不超过直径的一半$+1$
那么分类讨论
如果树的直径是奇数,那么直径的中点是一条边,那么以这条边左右两个端点分别作为两棵子树的根,统计每一层儿子数的最大值,在最后合并一下即可
如果树直径是偶数,那么直径的中点是一个节点,那么直接定这个中点为根,利用之前的做法统计出叶子节点个数,但是样例告诉我们还有另一种情况存在,由于此时直径为偶数,使直径$+1$并不会影响最小染色数,所以可以把直径$+1$,然后以边作为根,套用奇数的做法即可,最后取最小值即可
ARC105C Camels and Bridge
刚D去了比赛时候没想出来
由于$n$给得非常小,所以考虑枚举每一种骆驼的排列方式,那么对于一种固定的骆驼排列,可以发现由于每一只骆驼都要走过桥,在桥上的一定是骆驼排列中的一段区间,对于每一个区间两个端点的骆驼之间的距离是有限制的。具体地,对于区间$[L,R]$,$x_R-x_L\geq max(l_k)(v_k<\sum_{i=L}^{R} w_i)$,这个式子可以在m中二分找出答案,考虑如果满足这所有的条件,那么这种排列骆驼距离的方式一定合法。其实这个只要$L$向$R$连一条权值为$max(l_k)$的有向边,那么原问题就是找DAG上最长路(因为最长路保证了$u->v$所有其他的限制都被满足了),$dp$即可
复杂度$O(n!n^2logm)$
AGC46D Secret Passage
首先发现这个操作可以产生一些自由的$0$和$1$,这些可以任意的插入后面没有被操作影响到的串中,并且后面没有被操作影响到的串一定是原来串的后缀,那么记$ok[i][j][k]$为前$i$位被操作所影响到产生了$j$个自由$0$,$k$个自由$1$的状态是否合法,转移的时候枚举当前选出来的两个数,含多少个自由的$0$和多少个自由的$1$(0/1/2个),那么剩下的就是原来字符串里的$0,1$
然后再考虑将这些产生自由的$0,1$放到后缀里的方案数,记$dp[i][j][k]$表示$[i,n]$这个后缀未被操作所影响到,有$j$个自由$0$,有$k$个自由$1$插入其中的方案数,由于这个后缀一定是将$0,1$插入后得到串的子序列,那么考虑用子序列匹配的方式进行转移,就是$dp[i][j][k]$可以有$dp[i+1][j][k]$转移过来,然后如果当前这一位为$0$,可以向里面插$1$,可以有$dp[i][j][k-1]$转移过来,反之亦然
那么很自然的想,只要这个状态合法,就直接累计到答案中去,但这样会算重复,由于当后缀不断变成时,更长的后缀的方案一定被包含在短后缀的方案中(因为只要按顺序填$0,1$),那么从后往前扫描,每次有一个状态合法,将这个状态累计到答案中,之后把在这个基础上向前延伸的后缀的状态设为非法即可
AGC45C Range Set
好题,想了好久才想明白
首先0,1是对称的,可以把初始串变为全1,然后交换$a,b$,这个问题和原来的问题等价,那么可以通过这个性质保证$a \leq b $
然后考虑什么样子的串是合法的,首先发现如果有一段连续的1的个数$\geq b$那么通过这一段1,可以向左右两边扩展,考虑在扩展的过程中要添加一段连续的字符,如果这个长度大于对应的限制,那么直接赋就行了;如果小于,先将这一段赋上,然后会有一段覆盖到之前的已经固定的字符,由于之前第一次扩展保证合法,并且赋0操作不会把这个初始的$\geq b$的区间全部覆盖,不断用之前的步骤调整回来就可以。那么通过这种操作一定可以把除了这个初始1串的其余所有位置所有可能性统计到,再考虑这个$\geq b$的1串(当然最终可以得到的串可能不止一个$\geq b$的1串,此处只以一个举例),由于$a \leq b$,那么可以在结束扩展之后在这个1串里面操作出某几段$\geq a$的0串,这样的得到的串一定也是合法的
那么我们先假设把所有$\geq a$的0串都赋成1,最后把原来的方案数乘上去即可。考虑DP,由于直接DP不方便,那么考虑反面
首先可以通过一个DP求出所有长度为n的1串可以被$\geq a$的0串分割成多少种不同的串(注意这里要保证开头和结尾一定为1,否则会和左右两端其他的0合成更长的,这样会重复统计,但对于前缀后缀的1串,只要保证一段为1就可以了,另一端是0或1都可以),设$f[i][0/1]$表示长度为$i$的1串被分割后最后一位为$0/1$的方案数,初始条件$f[0][0]=1,f[0][1]=0$,保证第一段不为0
然后用$dp[i][0/1]$表示第$i$位为$0/1$方案数,转移的时候$0/1$最长长度只能为$a-1,b-1$,然后判断一下1串是否为前缀后缀,如果是那么系数为$f[len][0]+f[len][1]$,否则为$f[len][1]$
AGC44C Strange Dance
原来AGC也有数据结构题
考虑维护一个三进制Trie,对于S只要打标记交换1,2的位置,对于R,更新时先把当前节点的0,1,2换成2,0,1的顺序,然后考虑进位,递归更新2即可
AGC40C Neither AB nor BA
发现如果直接按题意去分析不能删AB或BA的性质,是很难的。由于不能删的是相邻的两个字母,那么考虑将偶数位的A改为B,B改为A,然后会发现题目变成了不能删AA或BB,那么只要A或B在序列中出现大于$\frac{n}{2}$次就一定不行,那么最终答案为$3^n-2\sum C_{n}^{i}2^{n-i} $
AGC16F Games on DAG
首先考虑每一个点求出其$sg$函数,只要$sg(1)=sg(2)$那么Alice必败,否则Alice必胜,那么先统计$sg(1)=sg(2)$的数量(因为数量少)可以发现,如果两个点的$sg$函数相同那么这些点之间一定没有边相连,那么就可以把点根据其$sg$函数值进行分层,并且要保证$1$号点和$2$号点要在同一层内,
由于n非常小,那么用状压来记录状态和枚举转移,记$dp[mask]$为当前$mask$点集已经在$sg$分层中的方案数,然后更新时枚举其子集作为最后一层$sg$的点,考虑具体如何转移,由于$sg$值较大的点一定要连向比其小$sg$层中至少一个点,那么枚举的当前子集,一定有其他已经在集合中的点连向它,那么计算出原来已经在集合中的点连向这些枚举的点的边的数量$w$,那么方案数就是$2^w-1$,然后当前枚举$sg$最小的这些点之间是不能连边的,但是可以连向$sg$函数值比它大的点,同样统计出边的数量,方案数为$2^w$
最终答案就是$dp[2^n-1]$
AGC2F Leftmost Ball
一开始搞出了$n^3$的dp,但并没有什么用
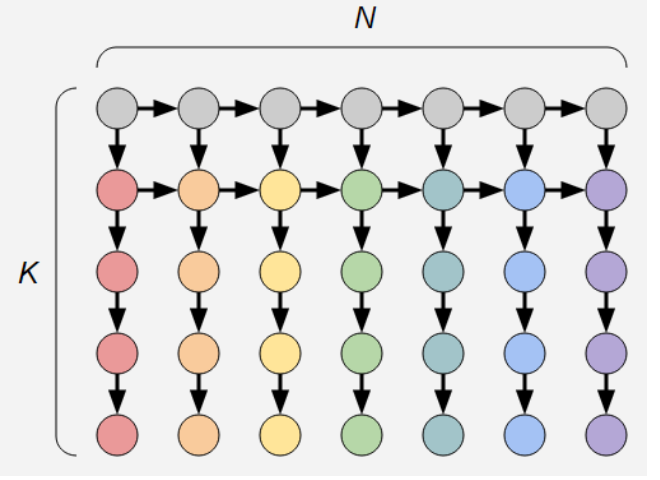
这种放球不同的序列并且放球之间有限制,那么可以看作有向图的拓扑序,用连边来表示限制
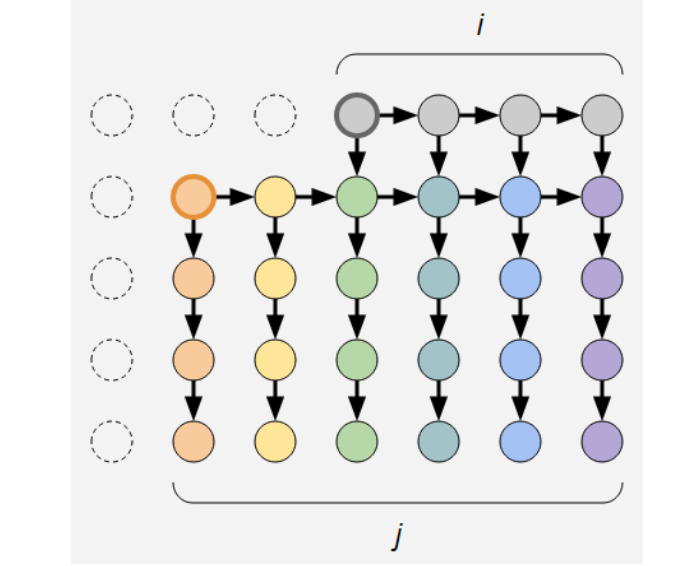
考虑单独领出每种颜色的第一个球,在放完这个第一个球之后才能放这个颜色其他的球,然后再限制要按顺序放不同颜色的第一个球,然后最终算出答案后乘上n!即可
那么可以构建出这样一个图,用dp求解其拓扑序数,当解锁新的一列时,将这一列中的球穿插到还没有解锁的球中,组合数计算可以得到
AGC48D Pocky Game
首先分析可以发现,如果某一个人当前的石子数大于剩余的石子数,那么这个人一定必胜
那么可以得到两个人的策略,要么直接放弃当前这一堆石子,去抢后面更大的石子,要么一个一个拿走当前堆中的石子,以拖延对手的时间
在这种策略下取不会出现取多个石子,却不取完当前石子的操作,因为这样会缩短拖延的时间
可以设$f[i][j][k]$表示区间$[i,j]$的石子,最左端的石子个数为$k$是否可以胜利
由于对于$k_1>k_2$,如果$k_2$可以获胜,那么$k_1$一定也可以,因为可以完全复制于$k_2$一样的操作
那么可以压缩状态,设$f[i][j]$表示$[i,j]$区间内,获胜所需最小左端石子数
同理$g[i][j]$表示需要获胜所需右端的最小石子数
考虑转移,以左端为例
如果$a[j]<g[i+1][j]$,那么左端的人直接放弃$a[i]$就可以获胜,那么$f[i][j]=1$
如果$a[j] \geq g[i+1][j]$,那么两个人开始拖延时间,各自都取一个石子,直到$a[j]=g[i+1][j]$时,右端的人此时必须放弃$a[j]$,否则会导致上面那种情况的产生,那么现在区间变成了$[i,j-1]$,那么先手获胜最小石子数$f[i][j-1]$,由于之前拿走了$a[j]-g[i+1][j]+1$个石子,那么$f[i][j]=f[i][j-1]+a[j]-g[i+1][j]+1$
$g$的转移同理
AGC30D Inversion Sum
这种套路还是没有完全理解啊
考虑设$dp[i][j]$表示$a_i>a_j$的方案数,然后按输入的操作进行转移,但是直接转移,不仅需要考虑$i,j=x[i],y[i]$的情况,还要把所有其他$i,j$方案数乘$2$,这样每一次是$O(n^2)$转移
注意到$i,j$不等于$x,y$的情况,每一次操作转移的瓶颈在这里,但是每一次操作都很简单只是对方案数$*2$,那么考虑将所有的$2$提取出来,最后算答案的时候再乘上去$2^q$
那么这样$dp$的意义就变为了概率
如果操作没有影响到$dp[i][j]$那么,$dp[i][j]$的概率就不变
那么只要考虑$i,j$等于$x$或$y$的情况,每一次转移$O(n)$


