多项式总结

多项式

一.常用卷积形式

·$a_{i}=\sum_{j=0}^{i} b_{i-j}c_{j}$

直接FFT/NTT

·$a_{i}=\sum_{j=1}^{i} a_{i}b_{i-j}$

分治FFT

·$a_{i}=\sum_{j=0}^{C} b_{i+j}c_{j}$

其中$C$为一个定值，那么将$c$翻转之后，$b$与$c$的下标之和即为一个定值，直接卷积，最终下标减去$C$

二.卷积的应用

主要是利用上面的形式来不断的变形

·卷积在字符串匹配中的应用

如果字符串中没有特殊作用的字符，那么可以直接用KMP或者AC自动机，但一旦有像通配符这样的字符时，就可以考虑构造卷积来实现

对于一般的字符串匹配，设$S,T$为两个字符串，$T$为文本串，$S$为模式串，$n$为$S$的长度（下标从0开始），可以构造如下的卷积形式

$f_{i}=\sum_{j=0}^{n-1}(T_{i+j}-S_{i})^{2}$

如果最终$f_{i}=0$那么说明$S$在$T$的$i$位置开始可以匹配，计算的话，直接利用上面的形式翻转计算即可 

P.S.这里利用平方的原因是，如果只用$T_{i+j}-S_{i}$的话，会存在正负抵消的情况，比如ab和ba会误判成匹配

如果存在通配符，那么直接在最后在乘上$S_{i}$即可，此处能取到0时当且仅当$S_{i}$与$T_{i+j}$相等，或$S_{i}$是一个通配符

·卷积模拟无限背包过程

在次数为物体体积那一项系数变为1，常数项系数变为1的多项式，这个多项式自乘多少次，就是从中选取多少个物体

如果能组成体积为$v$的物体，只有在第$v$项前的系数不为0时才可行

注意这个卷积的$len$一定要开到足够大，最大体积的两倍以上，因为DFT是循环卷积，超出len范围的次数，会对len取模叠加到前面项的系数上，导致程序误判

·卷积计算生成函数

如果是生成函数的项数是有限项，那么可以直接FFT乘起来，得到每一项前的系数

也可以用来化简生成函数的封闭形式

这部分做的不多……留坑

·卷积优化DP

当DP方程中出现卷积形式的时候，可以考虑使用FFT进行优化，但要注意下标的顺序和更新顺序

·卷积实现区间的平移

对于给定的若干段区间如果要集体向右平移多次（如果要向左平移则要翻转区间）那么可以构造一个多项式，让需要平移的长度对应的下标上将数组变为1，再将区间在另一个多项式上将能覆盖的点赋值为1（差分即可），然后将两个多项式卷积起来，得到的新的多项式，如果某一项前的系数不为1，那么这个点被平移后的区间覆盖到

三.多项式的操作

·DFT的合并（FFT）

$P(x)=A(x)+\text{i}B(x)$

$Q(x)=A(x)-\text{i}B(x)$

只要求出P的DFT就可以得到A,B的DFT结果

 

 

 

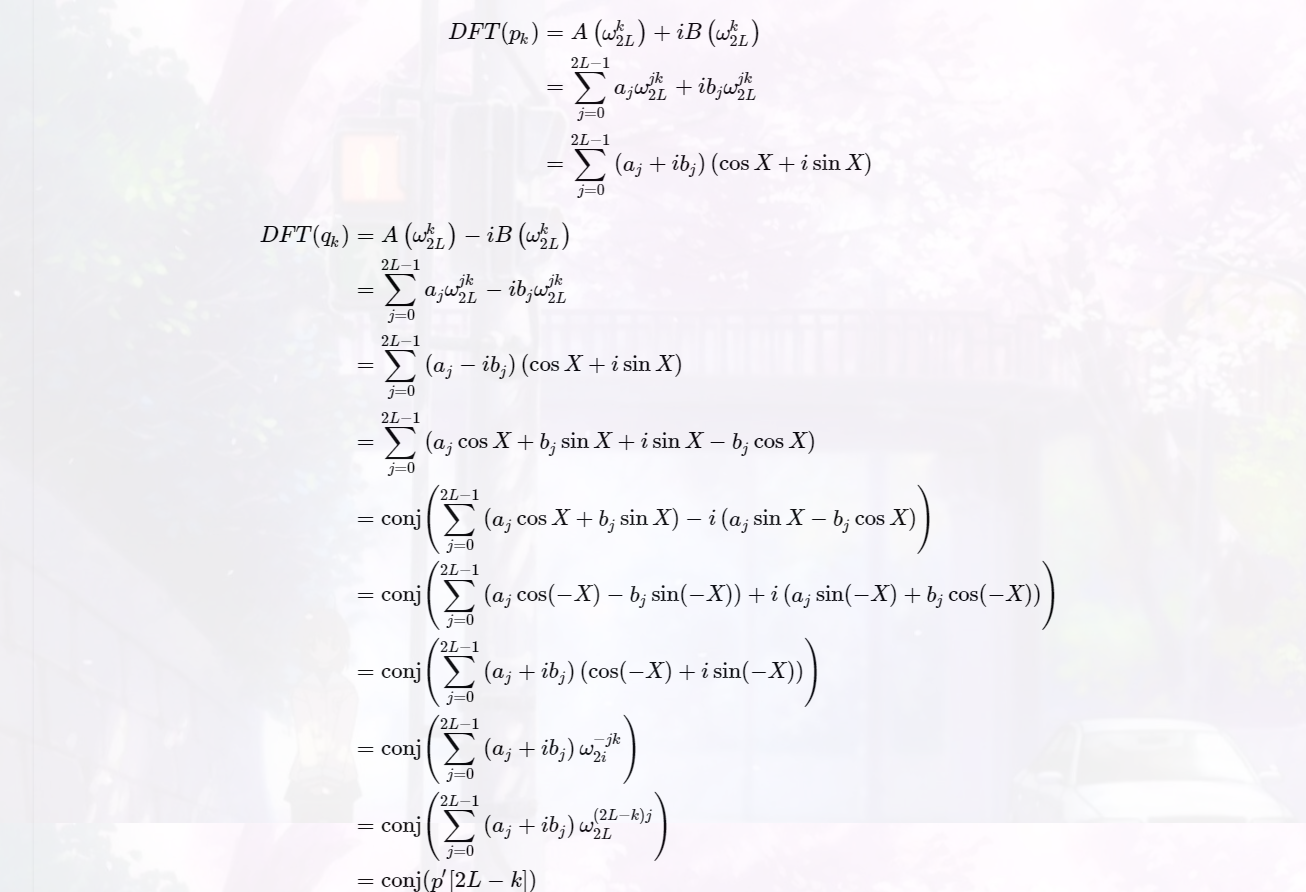
那么将$P$得到的结果区间翻转之后就是$Q$的结果

那么可以通过$P$，$Q$，DFT的结果来计算$A$，$B$，DFT后的结果

$DFT(a_k)=\frac{DFT(p_k)+DFT(q_k)}{2}=\frac{DFT(p_k)+\text{conj}(DFT(p_j))}{2}$

$DFT(b_k)=\text{i}\frac{DFT(p_k)-DFT(q_k)}{2}$

DFT合并部分转载于https://www.cnblogs.com/birchtree/p/12470386.html#

·多项式求逆