机器学习基石HOW部分(2)

机器学习基石HOW部分(2)

---

标签：机器学习基石

第十章

gradient descent on cross-entropy error to get good logistic hypothesis

从方程的形式、误差的衡量方式、如何最小化Ein的角度出发

之前提过的二元分类器如PLA，其目标函数为， f(x)=sign(wTx)∈−1,+1，输出要么是-1要么是+1，是一个“硬”的分类器。而Logistic Regression是一个“软”的分类器，它的输出是y=+1的概率，因此Logistic Regression的目标函数是 f(x)=P(+1|x)∈[0,1]。

方程的形式

logistic hypothesis: h(x)=θ(wTx)
logistic regression:h(x)=11+exp(−wTx)

有一组病人的数据，我们需要预测他们在一段时间后患上心脏病的“可能性”，就是我们要考虑的问题。
通过二值分类，我们仅仅能够预测病人是否会患上心脏病，不同于此的是，现在我们还关心患病的可能性，即 f(x) = P(+1|x)，取值范围是区间 [0,1]。
然而，我们能够获取的训练数据却与二值分类完全一样，x是病人的基本属性，y 是+1(患心脏病)或-1（没有患心脏病）。输入数据并没有告诉我们有关“概率” 的信息。
在二值分类中，我们得到一个”score” 后（s=∑i=0dwixi=wTx），通过取符号运算sign 来预测y 是+1 或 -1。而对于当前问题，我们如同能够将这个score 映射到[0,1] 区间，问题似乎就迎刃而解了。

θ(s)=es1+es=11+e−s

误差的衡量

Cross Entropy Error:err(w,x,y)=ln(1+exp(−ywx))

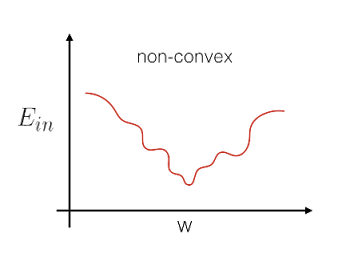
为什么不用上一章用到的平方误差，其实是因为Ein(w)=∑err就是一个关于w的非凸函数(non-convex),非凸函数由于存在很多个局部最小点，因此很难去做最优化(解全局最小)。所以Logistic Regression没有使用平方误差来定义error，而是使用极大似然法来估计模型的参数。

极大似然法基本思想：当从模型总体随机抽取n组样本观测值后，最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大，而不是像最小二乘估计法旨在得到使得模型能最好地拟合样本数据的参数估计量。

讲讲从视频中理解到的likelihood。一开始不懂，后来来来回回看了三遍，就完全理解了。
target function是f(x) = P(+1|x)
那么P(y|x)当y=+1和-1的时候，就有

P(y|x)={f(x)1−f(x)forfory=+1y=−1

现在假设有一个数据集D，D=(x1,+1),(x2,−1),……,(xN,−1).
f生成这个数据集的可能性是

P(x1)P(+1|x1)×P(x2)P(−1|x2)×...P(xN)P(−1|xN)

因为P(y|x)可以写成f(x)和1-f(x)的形式。
所以上式又可以变成

P(x1)f(x1)×P(x2)(1−f(x2))×...P(xN)(1−f(xN))

h生成这个数据集的likelihood是

P(x1)h(x1)×P(x2)(1−h(x2))×...P(xN)(1−h(xN))

假如h≈f，那根后两个式子可以得出 likelihood(h)≈ probability using f
g就是取likelihood最大的h。

logistic:h(x)=θ(wTx)那么就有1−h(x)=h(−x)
likelihood可以这样表达：

likelihood(h)=P(x1)h(x1)×P(x2)(−h(x2))×...P(xN)(−h(xN))

likelihood(logistic h) ∝∏n=1Nh(ynxn)
令上式最大，就可以得到最小的Ein,得到最好的g。

上面提到了h(x)=θ(wTx)，那likelihood(logistic h)∝∏n=1Nθ(ynwTxn)

我们不喜欢连乘，我们喜欢累加。我们不喜欢求最大值，我们热爱求最小值。
于是，把最大值取个对数，再添个负号，我们就可以愉快的求累加项的最小值了。

minw1N∑n=1N−lnθ(ynwTxn)

因为θ(s)=11+exp(s)所以

minw1N∑n=1N11+exp(ynwTxn)=minw1N∑n=1Nerr(w,xn,yn)

logistic regression的误差衡量–cross-entropy error终于出现了err(w,x,y) = ln(1 + exp(−ywx))

如何最小化Ein

Ein(w)=1N∑n=1Nln(1+exp(ynwTxn))

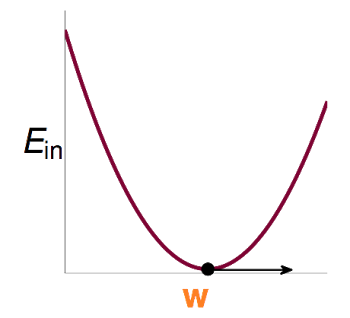
可以看出cost function是连续，可微的凸函数。按照之前Linear Regression的逻辑，由于它是凸函数，如果我们能解出一阶微分(梯度)为0的点，这个问题就解决了。

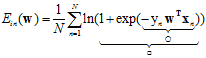
对权值向量w的单个分量求偏微分过程

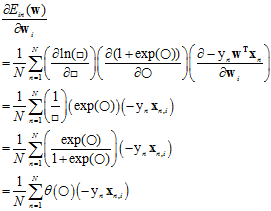
最终出来∇Ein(w)=1N∑Nn=1θ(−ynwTxn)(−ynxn)
离目标又近了一步，只要把上面式子=0，然后就可以得到最小的Ein了。
坏了，这个不是线性的。
和之前的Linear Regression不同，它不是一个线性的式子，要求解∇Ein(w)=0这个式子，是困难的。那么该使用何种方法实现Ein(w)最小化呢？
这里可以使用类似PLA当中的，通过迭代的方式来求解，这种方法又称为梯度下降法(Gradient Descent)。
For t = 0,1,…

wt+1←wt+ηv

when stop, return last w as g
其中η为每步更新的大小(step size)，v是单位向量，表示每次更新的方向。

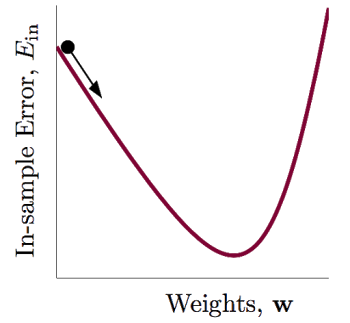
就好像有一个小球，从山上往下滚。当小球滚到谷底的时候，我们就有了最小的Ein。
小球滚动，需要我们明确两点，一是滚动的方向，二是滚动的步长。
方向很容易就可以确定了。因为我们要小球滚到谷底，当然方向要向着谷底啊。但是我们不知道谷底在哪里，所以就需要小球往海拔低的方向，也就是，小球在每一点的方向就是该点一阶微分后的向量所指的方向：

v=−farc∇Ein(wt)||∇Ein(wt)||

步长η比较难决定，太小了，更新太慢，太大了，一下子越过谷底，往对面走了。

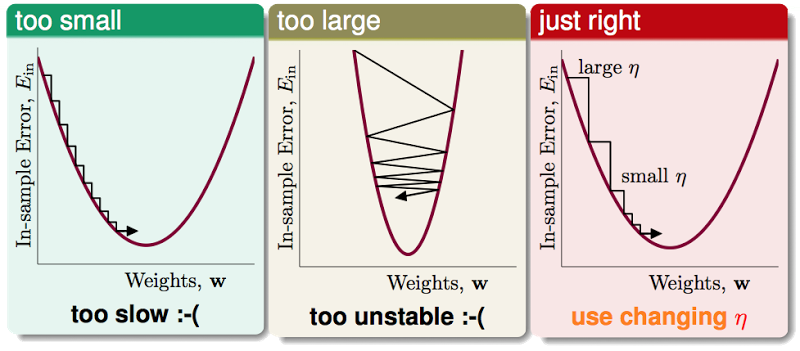
一个比较好的做法是让η与 ||▽Ein(wt)|| 成一定的比例，让新的和||▽Ein(wt)||成比例的斜体的 η 来代替原来粗体的 η
我们称这个斜体的η为 fixed learning rate
wt+1←wt−η ∇Ein(wt)||∇Ein(wt)||

wt+1←wt−η∇Ein(wt)

最后再来完整的梳理下梯度下降法(Gradient Descent):
  initialize w0
  For t = 0, 1, …
  1. compute
    ∇Ein(w)=1N∑Nn=1θ(−ynwTxn)(−ynxn)
  2. update by
    wt+1←wt−η∇Ein(wt)
  …until Ein(wt+1)=0or enough iterations
  return last wt+1 as g