欧拉之路Ⅳ
Problem 84
Monopoly odds

模拟一下即可
#include<bits/stdc++.h> using namespace std; queue<int> cc,ch; set<int> R,U,CC,CH; int ts(int k){ if(R.count(k))return 1; if(U.count(k))return 2; if(CH.count(k))return 3; if(CC.count(k))return 4; return 0; } int get_cc(int x){ int k=cc.front(); cc.pop();cc.push(k); if(k==1)return 0; if(k==2)return 10; return x; } int get_ch(int x){ int k=ch.front(); ch.pop();ch.push(k); if(k>=11)return x; switch(k){ case 1:return 0;//GO case 2:return 10;//JAIL case 3:return 11;//C1 case 4:return 24;//E3 case 5:return 38;//H2 case 6:return 5;//R1 case 7:{ while(ts(x)!=1){ (x+=41)%=40; } return x; break; } case 8:{ while(ts(x)!=1){ (x+=41)%=40; } return x; break; } case 9:{ while(ts(x)!=2){ (x+=41)%=40; } return x; break; } case 10:return (x-3+40)%40; } } void init(){ int a[20]; for(int i=1;i<=16;i++) a[i]=i; random_shuffle(a+1,a+17); for(int i=1;i<=16;i++) cc.push(a[i]); random_shuffle(a+1,a+17); for(int i=1;i<=16;i++) ch.push(a[i]); R.insert(5),R.insert(15),R.insert(25),R.insert(35); U.insert(12),U.insert(28); CH.insert(6),CH.insert(22),CH.insert(36); CC.insert(2),CC.insert(17),CC.insert(33); } void get(int &x){ if(x==30){ x=10; return; } if(ts(x)==3){ x=get_ch(x); return; } if(ts(x)==4){ x=get_cc(x); return; } return; } int cnt; int dice(){ int a=rand()%4 +1; int b=rand()%4 +1; if(a==b)cnt++; else cnt=0; return a+b; } const double MAX_T=10; int g[50],tot; struct node{ int id; double num; bool operator < (const node &x)const{ return num>x.num; } }result[50]; int tms=5; int main(){ srand(time(NULL)); init(); int now=0; while((double)clock()/CLOCKS_PER_SEC<MAX_T){ now+=dice(); (now+=40)%=40; if(cnt==3){ cnt=0; now=10; } get(now); tot++; g[now]++; } for(int i=0;i<40;i++){ result[i]=(node){i,1.0*g[i]/tot}; } sort(result,result+40); for(int i=0;i<40;i++){ printf("%d %.4lf\n",result[i].id,result[i].num); } return 0; }
Problem 85
Counting rectangles

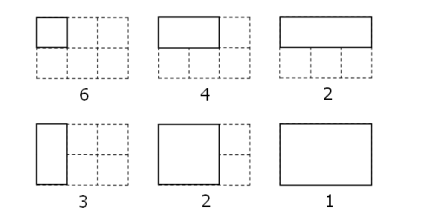
假设长方形长$x$宽$y$
则长的不同选择方法有$x*(x+1)/2$种
宽的不同选择方法有$y*(y+1)/2$种
所以总共就有$x*(x+1)/2*y*(y+1)/2$种,
可以$O(n^2)$求解,但是考虑更高效的方法,我们枚举$x$即可,$y$可以通过二分得到,然后$±1$求一下即可
时间复杂度$O(n \log n)$
#include<bits/stdc++.h> #define int long long using namespace std; const int p=1e9; int ans=1e9,k,S; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ k=read(); for(int i=1;;i++){ int x=(i+1)*i/2; if(x>k+k/2)break; int l=1,r=k; while(l<=r){ int mid=(l+r)>>1; int y=(1+mid)*mid/2; if(y*x>=k)r=mid-1; else l=mid+1; } if(abs(k-(r+1)*r/2*x)<abs(k-ans)){ ans=(r+1)*r/2*x; S=i*r; } r++; if(abs(k-(r+1)*r/2*x)<abs(k-ans)){ ans=(r+1)*r/2*x; S=i*r; } } cout<<S; return 0; }
Problem 85
Cuboid route
首先对于任意一个长方体,假设他的长宽高分别为$a,b,c$
那么对角线的走法肯定只有三种,即
$\sqrt{(a+b)^2+c^2}$
$\sqrt{(a+c)^2+b^2}$
$\sqrt{(b+c)^2+a^2}$
假设我们现在令第一种方式是最短路径,则可以推出
$2ab \leq 2ac \leq 2bc$从而得到$a \leq b \leq c$
我们这里可以枚举$c$,把$ab=a+b$看成一个整体显然$2 \leq ab \leq 2c$
然后内层枚举$ab$,判断一下是否是勾股数,再考虑怎么分配(注意$a=1,b=3$和$a=3,b=1$算同一种分配)
若$ab < c$那么显然可以取完,那么贡献就是$\lfloor \frac{ab}{2} \rfloor$
若$ab \geq c$那么就要满足$ab-c \leq b \leq c$所以贡献就是$(2*c-ab+1+1)/2$
(解释一下上面那个怎么来的,因为$b$有$c-(ab-c)+1$种取值,每一种取值$c$都会对应这个范围内的取值,所以要$/2$但是由于$b=c$的特殊情况下取整会取掉,所以再$+1$维护)
#include<bits/stdc++.h> #define int long long using namespace std; int m; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ m=read(); int cnt=0,c=1; while(cnt<m){ c++; for(int ab=1;ab<=2*c;ab++){ int p=ab*ab+c*c; int tmp=sqrt(p); if(tmp*tmp==p){ cnt+=(ab>=c)?(2*c-ab)/2+1:ab/2; } } } printf("%d",c); return 0; }
Problem 87
Prime power triples

先欧拉筛素数,然后暴力枚举判断
#include<bits/stdc++.h> using namespace std; const int N=10000; int n,MAX,len,ans; int v[N],p[N]; bool used[50000010]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void get_prime(){ for(int i=2;i<=MAX;i++){ if(!v[i])p[++len]=i; for(int j=1;j<=len&&p[j]*i<=MAX;j++){ v[p[j]*i]=1; if(i%p[j]==0)break; } } } int main(){ n=read(); MAX=sqrt(n); get_prime(); for(int i=1;i<=len;i++){ int x=p[i]*p[i]; if(x>n)break; for(int j=1;j<=len;j++){ int y=p[j]*p[j]*p[j]; if(x+y>n)break; for(int l=1;l<=len;l++){ int z=p[l]*p[l]*p[l]*p[l]; if(x+y+z>n)break; if(!used[x+y+z])used[x+y+z]=1,ans++; } } } cout<<ans; return 0; }
Problem 88
Product-sum numbers
对于一个$k$一定从$k+1$开始枚举才有可能是有效的,然后就是纯搜索,剪剪枝就跑过去了
#include<bits/stdc++.h> #define int long long using namespace std; int answer; set<int>::iterator it; set<int>ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void write(int x){ if(x<0)putchar('-'),x=-x; if(x>9)write(x/10); putchar(x%10+'0'); } bool check(int x,int y,int d){//积 和 digit if(y<d)return false; if(x==1)return y==d; if(d==1)return x==y; for(int i=1;i*i<=x;i++)if(x%i==0){ if(i!=1&&check(x/i,y-i,d-1))return 1; int xx=x/i; if(check(i,y-xx,d-1))return 1; } return 0; } int get(int n){ for(int i=n+1;;i++) if(check(i,i,n))return i; } signed main(){ int n=read(); for(int i=2;i<=n;i++){ int k=get(i); ans.insert(k); } for(it=ans.begin();it!=ans.end();it++) answer+=*it; write(answer); return 0; }
Problem 89
Roman numerals
可以把他给的罗马数字强制转化成数字然后再转换成罗马数字
#include<bits/stdc++.h> using namespace std; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void write(int x){ if(x<0)putchar('-'),x=-x; if(x>9)write(x/10); putchar(x%10+'0'); } char s[10010]; int v[3][10]={0,1,2,3,2,1,2,3,4,2, 0,1,2,3,2,1,2,3,4,2, 0,1,2,3,2,1,2,3,4,2}; int ans,sum; int main(){ while(~scanf("%s",s+1)){ if(s[1]=='P')break; int n=strlen(s+1),res=0; for(int i=1;i<=n;i++){ switch(s[i]){ case 'M':{ res+=1000; break; } case 'D':{ res+=500; break; } case 'C':{ if(i!=n&&(s[i+1]=='M'||s[i+1]=='D'))res-=100; else res+=100; break; } case 'L':{ res+=50; break; } case 'X':{ if(i!=n&&(s[i+1]=='L'||s[i+1]=='C'))res-=10; else res+=10; break; } case 'V':{ res+=5; break; } case 'I':{ if(i!=n&&(s[i+1]=='V'||s[i+1]=='X'))res--; else res++; break; } } } ans+=res/1000; res%=1000; ans+=v[0][res%10]; ans+=v[1][res/10%10]; ans+=v[2][res/100]; sum+=n; } write(sum-ans); return 0; }
其实有另一种更简单的方法,考虑能简化的只有
DCCCC ---> CM
LXXXX ---> XC
VIIII ---> IX
IIII ---> VI
XXXX --->XL
CCCC ---> CD
因为都是两个,随便找个东西就代替了
#include<bits/stdc++.h> using namespace std; string s; string ss="AA"; string f[6]={"DCCCC","LXXXX","VIIII","IIII","XXXX","CCCC"}; int ans; int main(){ while(cin>>s){ if(s=="P")break; int a=s.size(); for(int i=0;i<6;i++){ int p=s.find(f[i]); while(p!=-1){ s.replace(p,f[i].size(),ss); p=s.find(f[i]); } } ans+=a-s.size(); } cout<<ans<<endl; return 0; }
Problem 90
Cube digit pairs
搜索啊,暴力啊,但是方案数要除以二,可能重复,搜索也保证递增即可
#include<bits/stdc++.h> using namespace std; int ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void write(int x){ if(x<0)putchar('-'),x=-x; if(x>9)write(x/10); putchar(x%10+'0'); } int ina[10],inb[10]; int v[10][2]={0,0,0,1,0,4,0,9,1,6,2,5,3,6,4,9,6,4,8,1}; void dfsb(int k,int pre){ if(k==7){ int f=1; for(int i=1;i<=9;i++){ if(ina[v[i][0]]&&inb[v[i][1]]||ina[v[i][1]]&&inb[v[i][0]]); else f=0; } ans+=f; return ; } for(int i=pre;i<=9;i++){ inb[i]++; if(i==6)inb[9]++; if(i==9)inb[6]++; dfsb(k+1,i+1); inb[i]--; if(i==6)inb[9]--; if(i==9)inb[6]--; } return; } void dfs(int k,int pre){ if(k==7){ dfsb(1,0); return ; } for(int i=pre;i<=9;i++){ ina[i]++; if(i==6)ina[9]++; if(i==9)ina[6]++; dfs(k+1,i+1); ina[i]--; if(i==6)ina[9]--; if(i==9)ina[6]--; } return; } int main(){ dfs(1,0); cout<<ans/2; return 0; }
Problem 91
Right triangles with integer coordinates
$O(n^4)$枚举,注意不能重点,共线可以不判断,最后答案除以二
#include<bits/stdc++.h> using namespace std; int ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int main(){ int n=read(); for(int i=0;i<=n;i++){ for(int j=0;j<=n;j++){ for(int x=0;x<=n;x++){ for(int y=0;y<=n;y++){ if(i==x&&j==y)continue; if(x==0&&y==0)continue; if(i==0&&j==0)continue; int a=i*i+j*j; int b=x*x+y*y; int c=(i-x)*(i-x)+(j-y)*(j-y); if(a+b==c||a+c==b||b+c==a)ans++; } } } } cout<<ans/2; return 0; }
Problem 92
Square digit chains
记忆化搜索即可
#include<bits/stdc++.h> using namespace std; const int N=20000000; short ans[N]; int sq[10]={0,1,4,9,16,25,36,49,64,81}; int get(int x){ if(ans[x])return ans[x]; int p=x,res=0; while(p){ res+=sq[p%10]; p/=10; } return ans[x]=get(res); } int main(){ int n,answer=0; ans[1]=1,ans[89]=89; scanf("%d",&n); for(int i=1;i<=n;i++){ ans[i]=get(i); if(ans[i]==89)answer++; } cout<<answer; return 0; }
Problem 93
Arithmetic expressions
搜索一下,枚举选的数,然后全排列,再枚举符号,注意第一个可能是负的

#include<bits/stdc++.h> using namespace std; int ans,x,y,z,m; int a[50]; int op[50]; bool vis[100010]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } void work(int k){ if(k==4){ int fz=((op[0]==1)?1:-1)*a[1],fm=1; for(int i=2;i<=4;i++){ switch(op[i-1]){ case 1:{ fz=fz+fm*a[i]; break; } case 2:{ fz=fz*a[i]; break; } case 3:{ fm*=a[i]; break; } case 4:{ fz=fz-fm*a[i]; break; } } } if(fz<0)return; int GCD=__gcd(fm,fz); fm/=GCD,fz/=GCD; if(fm==1)vis[fz]=1; return; } for(int i=1;i<=4;i++) op[k]=i,work(k+1); return; } void check(){ memset(vis,0,sizeof vis); do{ op[0]=1; work(1); op[0]=0; work(1); }while(next_permutation(a+1,a+1+4)); } void find_(int k,int pre){ if(k==5){ check(); for(int i=1;;i++){ if(!vis[i]){ if(i-1>ans){ ans=i-1; x=a[1],y=a[2],z=a[3],m=a[4]; } break; } } return; } for(int i=pre;i<=9;i++){ a[k]=pre; find_(k+1,i+1); } } int main(){ find_(1,1); printf("%d\n%d %d %d %d",ans,x,y,z,m); return 0; }
Problem 94
Almost equilateral triangles

假设边长分别为$x,x,x+1$
那么$p=\frac{3x+1}{2}$
$S=\sqrt{p(p-x)(p-x)(p-x-1)}$
所以$p(p-x-1)$是平方数
所以有$3x^2-2x-1=y$,$y$是平方数,前面那个分母为$4$本来也是平方数,所以保证$y$是偶数即可
然后就解一个一元二次方程,因为边长是正的,所以
$x=\frac{1+\sqrt{3y+4} }{3}$
我们只需要枚举$\sqrt{3y+4}$进而判断$y$是否合法,然后计算答案就行
若$x,x,x-1$的边长,只变了前面那个$1$的符号
#include<bits/stdc++.h> #define int long long using namespace std; int ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline bool check(int x){ int xx=sqrt(x); return xx*xx==x; } signed main(){ int n=read(); for(int i=1;;){ if((i+1)%3==0)i+=2; else if((i-1)%3==0)i++; int z=i*i; if((z-4)%3)continue; int y=(z-4)/3; if(!check(y))continue; int x1=(i+1)/3; int x2=(i-1)/3; if(3*x2>n||3*x1>n)break; if((i+1)%3==0 and x1>1)ans+=3*x1+1,cout<<x1<<" +1"<<endl; if((i-1)%3==0 and x2>2)ans+=3*x2-1,cout<<x2<<" -1"<<endl; } printf("%lld",ans); return 0; }
Problem 95
Amicable chains

拿一个栈判环,把环上的全都赋值,不是环上的就变成-1,保证每个数只会被搜到一次
至于真因数和线性筛即可
#include<bits/stdc++.h> using namespace std; const int N=10000010; int n,answer,id,len; int v[N]; int in[N]; int ans[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int g[N],d[N],p[N]; inline void get_d(){ g[1]=d[1]=1; for(int i=2;i<=n;i++){ if(!v[i]) p[++len]=i,d[i]=i+1,g[i]=i+1; for(int j=1;j<=len&&p[j]*i<=n;j++){ v[p[j]*i]=1; if(i%p[j]==0){ g[i*p[j]]=g[i]*p[j]+1; d[i*p[j]]=d[i]/g[i]*g[i*p[j]]; break; } d[i*p[j]]=d[i]*d[p[j]]; g[i*p[j]]=1+p[j]; } } for(int i=1;i<=n;i++) d[i]-=i; } int s[N],top; void get(int x,int dep){ if(x>n)return; if(ans[x]){ while(top) ans[s[top--]]=-1; return; } if(in[x]){ int len=dep-in[x]; while(s[top]!=x) ans[s[top--]]=len; ans[s[top--]]=len; while(top) ans[s[top--]]=-1; return; } s[++top]=x; in[x]=dep; get(d[x],dep+1); in[x]=0; return; } int main(){ n=read(); get_d(); for(int i=1;i<=n;i++){ top=0; get(i,1); if(ans[i]>answer){ answer=ans[i]; id=i; } } cout<<id<<" "<<answer; return 0; }
Problem 96
Su Doku
就是一道简单搜索,拿一个数组打标记就行了
#include<bits/stdc++.h> using namespace std; int f,ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } char s[11][11]; int a[11][11]; int X[11],Y[11],sq[11]; inline int get_sq(int x,int y){ x=(x-1)/3; y=(y-1)/3+1; return x*3+y; } void prepare(){ for(int i=1;i<=9;i++){ for(int j=1;j<=9;j++){ if(s[i][j]=='0')continue; a[i][j]=s[i][j]-'0'; X[i]^=(1<<s[i][j]-'0'); Y[j]^=(1<<s[i][j]-'0'); sq[get_sq(i,j)]^=(1<<s[i][j]-'0'); } } return; } void dfs(int x,int y){ if(f)return; if(y==10)x++,y=1; if(x==10){f=1;ans+=a[1][1]*100+a[1][2]*10+a[1][3];return;} if(s[x][y]!='0'){ dfs(x,y+1); return; } for(int i=1;i<=9;i++){ if((X[x]>>i)&1)continue; if((Y[y]>>i)&1)continue; if((sq[get_sq(x,y)]>>i)&1)continue; X[x]^=1<<i,Y[y]^=1<<i; sq[get_sq(x,y)]^=1<<i; a[x][y]=i; dfs(x,y+1); X[x]^=1<<i,Y[y]^=1<<i; sq[get_sq(x,y)]^=1<<i; } } signed main(){ for(int i=1;i<=50;i++){ memset(X,0,sizeof X); memset(Y,0,sizeof Y); memset(a,0,sizeof a); memset(sq,0,sizeof sq); f=0; scanf("%s%s",s[0],s[0]); for(int i=1;i<=9;i++) scanf("%s",s[i]+1); prepare(); dfs(1,1); } cout<<ans<<endl; return 0; }
Problem 97
Large non-Mersenne prime
根据题意,注意不能快速幂,会炸,直接循环然后取余即可
#include<bits/stdc++.h> #define int long long using namespace std; const int p=10000000000; int ans=1; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ int base=7830457; while(base--){ ans=ans*2%p; } ans=ans*28433%p; ans++; cout<<ans; return 0; }
Problem 99
有$x=a^{log_a(x)}$
所以$x^y=a^{log_a(x)*y}$
因为底数$a$相同,所以我们只需要比较指数就能比较出大小
#include<bits/stdc++.h> #define int long long using namespace std; int id,MAX; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ for(int i=1;i<=1000;i++){ int x=read(),y=read(); int n=(log2(x)*y); if(n>MAX){ MAX=n,id=i; } } cout<<id; return 0; }

