欧拉之路III
Problem 51

枚举每一位放数字还是放未知的,如果为止的就拿1代替单独存
因为要有8个,所以我们可知未知的一定是三的倍数,末尾一定是1,3,7,然后暴力搞一搞(剪枝跑得飞快)
1 #include<bits/stdc++.h> 2 #define reg register 3 #define int long long 4 using namespace std; 5 int last[3]={1,3,7}; 6 bool check(int x){//判断素数 7 if(x==1||(x%6!=1&&x%6!=5)) 8 return 0; 9 if(x==2||x==3)return 1; 10 int MAX=sqrt(x); 11 for(int i=5;i<=MAX;i+=6) 12 if(x%i==0||x%(i+2)==0) 13 return 0; 14 return 1; 15 } 16 void dfs(int k,int unknow,int know,int rest){//第几位 未知的放的位置 已知的 还剩几个未知的 17 if(k-1<rest)return;//最后一位不放未知的 18 if(k==1){ 19 for(int p=0;p<3;p++){//枚举最后一位 20 int f=0,ans=0; 21 for(reg int i=0;i<=9;i++) 22 if(check((know+unknow*i)*10+last[p])){ 23 if(unknow>know&&i==0)ans--; 24 ans++; 25 if(!f)f=(know+unknow*i)*10+last[p]; 26 if(ans+(9-i)<8)break; //如果剩下全是还没有8个就退出 27 } 28 if(ans==8){//输出答案 29 printf("%d\n",f); 30 exit(0); 31 } 32 f=0,ans=0; 33 } 34 return; 35 } 36 for(reg int i=0;i<=9;i++) 37 dfs(k-1,unknow*10,know*10+i,rest);//继续搜索 38 dfs(k-1,unknow*10+1,know*10,rest-1); 39 return; 40 } 41 signed main(){ 42 for(reg int k=1;;k++){ 43 for(reg int l=3;l<k;l+=3) 44 dfs(k,0,0,l); 45 } 46 return 0; 47 }
Problem 52
可以看出,125874和它的两倍251748拥有同样的数字,只是排列顺序不同。
有些正整数x满足2x、3x、4x、5x和6x都拥有相同的数字,求其中最小的正整数。
可知$x,6x$位数相同,所以加一个小小的剪枝,然后暴力判断
1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 int n=1e5; 5 bool check(int x){ 6 int a=x,f=0; 7 while(a){ 8 f+=pow(10,a%10); 9 a/=10; 10 } 11 for(int i=2;i<=6;i++) 12 { 13 a=x*i; 14 int ff=0; 15 while(a){ 16 ff+=pow(10,a%10); 17 a/=10; 18 } 19 if(ff!=f)return false; 20 } 21 return true; 22 } 23 signed main() 24 { 25 while(1){ 26 for(int i=n;i*6<n*10;i++){ 27 if(check(i)){ 28 printf("%d\n",i); 29 goto ed; 30 } 31 } 32 33 n*=10; 34 } 35 ed: 36 return 0; 37 }
Problem 53

首先你得知道$\binom{n}{r}=\binom{n}{n-r}=\frac{n!}{r!(n-r)!}$
当$r\leq \lfloor \frac{n}{2} \rfloor$时,这个值是不会下降的,然后找到递推式
然后找到 最大的直接计算就行了
Problem 55
暴力stringstream转换然后判断回文即可
#include<bits/stdc++.h> #define int long long using namespace std; int ans,tag; bool check(int x){ for(int i=1;i<=60;i++){ bool f=1; int nt=0; stringstream ss; string s; ss<<x; ss>>s; int len=s.size()-1; for(int i=0;i<=len;i++){ nt=nt*10+s[i]+s[len-i]-'0'-'0'; if(s[i]!=s[len-i])f=0; } if(f&&i!=1){ return f; } x=nt; } return false; } signed main(){ for(tag=1;tag<=10000;tag++){ if(!check(tag))ans++; } printf("%d",ans); return 0; }
Problem 57
找到分子分母的变化规律然后枚举
#include<bits/stdc++.h> #define int long long using namespace std; int fz=3,fm=2,ans; signed main(){ for(int i=2;i<=1000;i++){ if((int)log10(fz)>(int)log10(fm))ans++; fz+=fm; swap(fz,fm); fz+=fm; if(fz>1e16)fz/=100,fm/=100; } cout<<ans; return 0; }
Problem 58
找到右上角那个数的变化规律,然后推出剩下三个数,判断素数一下再看占比多少
#include<bits/stdc++.h> #define int long long using namespace std; int a=3,b=5,c=7,d=9,ans=3,tag; bool check(int n) { if(n==1)return false; if(n==2||n==3)return true; if(n%6!=1&&n%6!=5)return false; for(int i=5;i*i<=n;i+=6) { if(n%i==0||n%(i+2)==0)return false; } return true; } signed main(){ for(tag=3;;tag+=2){ a=a+(tag-1)*4+2; b=a+tag+1; c=b+tag+1; d=c+tag+1; ans=ans+check(a)+check(b)+check(c)+check(d); int bili=(ans*100)/(tag+tag-1); if(bili<10)break; } cout<<tag; return 0; }
Problem 59

枚举三位密匙,去匹配,然后找关键词 the 如果有就输出
#include<bits/stdc++.h> using namespace std; int n; int s[1001]; char ans[1001]; char i[1001]; inline int read(){ int x=0; char ch=getchar(); while(!isdigit(ch)){ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x; } signed main(){ freopen("1.txt","r",stdin); for(;;){ s[++n]=read(); } for(i[1]='a';i[1]<='z';i[1]++){ for(i[2]='a';i[2]<='z';i[2]++){ for(i[3]='a';i[3]<='z';i[3]++){ for(int m=1;m<=n;m++){ ans[m]=(char)s[m]^i[((m-1)%3)]; } for(int m=4;m<=n;m++){ if(ans[m-3]=='t'&&ans[m-2]=='h'&&ans[m-1]=='e') { for(int p=1;p<=n;p++){ cout<<ans[p]; } cout<<endl; break; } } } } } return 0; }
Problem 60
先筛质数,然后枚举判断,加一个小剪枝:除去3那个质数,剩下对3取余必须相同,不然肯定没有质数
#include<bits/stdc++.h> #define intt long long using namespace std; int p[10000010],v[10000010],len,ans; void get(int n){ for(int i=2;i<=n;i++){ if(v[i]==0){ len++; p[len]=i; } for(int j=1;j<=len&&i*p[j]<=n;j++){ v[i*p[j]]=1; if(i%p[j]==0)break; } } } int f(int num) { if(num==1)return 1; if(num==2||num==3)return 0; if(num%6!=1&&num%6!=5)return 1; int tmp=sqrt(num); for(int i=5;i<=tmp;i+=6) if(num%i==0||num%(i+2)==0) return 1; return 0; } bool check(int l,int r){ int a=pow(10,(int)log10(l)+1)*r+l; int b=pow(10,(int)log10(r)+1)*l+r; return f(a)||f(b); } signed main() { get(10000); for(int i=1;i<=len;i++){ for(int j=i+1;j<=len;j++){ if(p[j]%3!=p[i]%3&&p[i]!=3)continue; if(check(p[i],p[j]))continue; for(int l=j+1;l<=len;l++){ if(p[l]%3!=p[j]%3)continue; if(check(p[l],p[i])||check(p[l],p[j]))continue; for(int k=l+1;k<=len;k++){ if(p[k]%3!=p[j]%3)continue; if(check(p[k],p[i])||check(p[k],p[j])||check(p[k],p[l]))continue; for(int m=k+1;m<=len;m++){ if(p[m]%3!=p[j]%3)continue; if(check(p[m],p[i])||check(p[m],p[j])||check(p[m],p[l])||check(p[m],p[k]))continue; cout<<p[i]<<" "<<p[j]<<" "<<p[l]<<" "<<p[k]<<" "<<p[m]<<endl; } } } } } printf("%lld",ans); }
Problem 61
二分找一下即可,注意每个类型的数顺序可能不一样,所以全排列枚举一下
1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[100]; 4 inline int check(int n,int flag){ 5 switch(flag){ 6 case 1:return n*(n+1)/2; 7 case 2:return n*n; 8 case 3:return n*(3*n-1)/2; 9 case 4:return n*(2*n-1); 10 case 5:return n*(5*n-3)/2; 11 case 6:return n*(3*n-2); 12 } 13 } 14 int find_(int x,int flag){ 15 int l=1,r=400; 16 while(l<=r){ 17 int mid=(l+r)>>1; 18 if(check(mid,flag)>=x)r=mid-1; 19 else l=mid+1; 20 } 21 return r+1; 22 } 23 int main(){ 24 a[1]=1; 25 a[2]=2; 26 a[3]=3; 27 a[4]=4; 28 a[5]=5; 29 a[6]=6; 30 do{ 31 for(int i1=find_(1000,a[1]);check(i1,a[1])<=9999;i1++){ 32 if(check(i1,a[1])%100<10)continue; 33 for(int i2=find_(check(i1,a[1])%100*100,a[2]);check(i2,a[2])/100==check(i1,a[1])%100;i2++){ 34 if(check(i2,a[2])%100<10)continue; 35 for(int i3=find_(check(i2,a[2])%100*100,a[3]);check(i3,a[3])/100==check(i2,a[2])%100;i3++){ 36 if(check(i3,a[3])%100<10)continue; 37 for(int i4=find_(check(i3,a[3])%100*100,a[4]);check(i4,a[4])/100==check(i3,a[3])%100;i4++){ 38 if(check(i4,a[4])%100<10)continue; 39 for(int i5=find_(check(i4,a[4])%100*100,a[5]);check(i5,a[5])/100==check(i4,a[4])%100;i5++){ 40 if(check(i5,a[5])%100<10)continue; 41 int i6=check(i5,a[5])%100*100+check(i1,a[1])/100; 42 if(check(find_(i6,a[6]),a[6])==i6){ 43 cout<<check(i1,a[1])<<" "<<check(i2,a[2])<<" "<<check(i3,a[3])<<" "<<check(i4,a[4])<<" "<<check(i5,a[5])<<" "<<i6<<" "<<endl; 44 } 45 } 46 } 47 } 48 } 49 } 50 }while(next_permutation(a+1,a+1+6)); 51 return 0; 52 }
Problem 62
map存这个立方数的数字被用过几次,超过五次就返回
#include<bits/stdc++.h> #define int long long using namespace std; map<int,int>mp,ans; signed main(){ for(int i=1;;i++){ int a=i*i*i,res=0; while(a){ res+=pow(10,a%10); a/=10; } mp[res]++; if(mp[res]==5){ cout<<ans[res]; return 0; } if(mp[res]==1)ans[res]=i*i*i; } }
Problem 63

首先只可能一位数满足,枚举判断即可,不合法就退出
#include<bits/stdc++.h> #define int long long using namespace std; int ans; signed main(){ for(int i=1;i<=9;i++){ for(int j=1;(int)log10(pow(i,j))+1==j;j++) ans++; } cout<<ans; }
Problem 64
根据每次变化,分子分母互换,分母有理化,变成真分数加上整数,然后继续对剩下的分数做这个操作
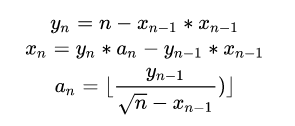
注意根号的系数和分母要约分
#include<bits/stdc++.h> #define pi pair<int,int> #define pii pair<int,pi > #define mk(x,y,z) pii(x,pi(y,z)) using namespace std; int n=10000; int x,y,a,len,ans,tag; map<pii,int>mp; void check(int a,int x,int y,int d){ // cout<<tag<<" "<<a<<" "<<x<<" "<<y<<" "<<endl; pii h; h=mk(a,x,y); if(mp[h]){ len=d-mp[h]; return; } mp[h]=d; int a_=(int)((double)y/(sqrt(tag)-x)); int y_=tag-x*x; int x_=y_*a_-y*x; int GCD=__gcd(y,y_); x_/=GCD; y_/=GCD; check(a_,x_,y_,d+1); } int main(){ for(tag=1;tag<=n;tag++){ if((int)sqrt(tag)*(int)sqrt(tag)==tag)continue; mp.clear(); check((int)sqrt(tag),(int)sqrt(tag),1,1); ans+=len%2; len=0; } cout<<ans; return 0; }
Problem 65
Convergents of e

首先为了方便,我们可以转换成$[1,1,2,1,1,4,...]$然后再加上一,考虑从最后一个数入手,当它作为分母的时候,此时分子是1,所以需要分子分母互换$\frac{1}{\frac{a}{b}}=\frac{b}{a}$然后加上前一个数$a_{i-1}$得到新的$\frac{a'}{b'}$此时他又是分母,一直做下去即可
#include<bits/stdc++.h> #define int_ node using namespace std; long long ans; struct node{ int a[100010]; node(){ memset(a,0,sizeof a); } node operator+(const node &x){ node y; for(int i=1;i<=1000;i++){ y.a[i]+=x.a[i]+a[i], y.a[i+1]+=y.a[i]/10, y.a[i]%=10; } return y; } node operator*(const int x){ node y; for(int i=1;i<=1000;i++) y.a[i]+=a[i]*x; return y; } }; int n; node fz,fm; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ n=read(); int k=n/3*2; fm.a[1]=1; for(int i=n;i>=1;i--){ if(i%3==0){ fz=fz+fm*k; k-=2; } else fz=fz+fm; swap(fz,fm); } swap(fz,fm); fz=fz+fm; for(int i=100;i>=1;i--) ans+=fz.a[i]; cout<<ans; return 0; }
Problem 66
Diophantine equation
这是一个pell方程,要利用连分数解决问题
#include<bits/stdc++.h> #define int long long using namespace std; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int a[20000]; bool pell_minimum_solution(int n,int &x0,int &y0){ int m=(int)sqrt((double)n); double sq=sqrt(n); int i=0; if(m*m==n)return false; a[i++]=m; int b=m,c=1; double tmp; do{ c=(n-b*b)/c; tmp=(sq+b)/c; a[i++]=(int)(floor(tmp)); b=a[i-1]*c-b; }while(a[i-1]!=2*a[0]); int p=1,q=0; for(int j=i-2;j>=0;j--){ int t=p; p=q+p*a[j]; q=t; } if((i-1)%2==0){x0=p;y0=q;} else{x0=2*p*p+1;y0=2*p*q;} return true; } signed main(){ int n,x,y; while(~scanf("%lld",&n)){ if(pell_minimum_solution(n,x,y)){ printf("%lld^2-%lld*%lld^2=1\t",x,n,y); printf("%lld-%lld=1\n",x*x,n*y*y); } } return 0; }
Problem 68
Magic 5-gon ring
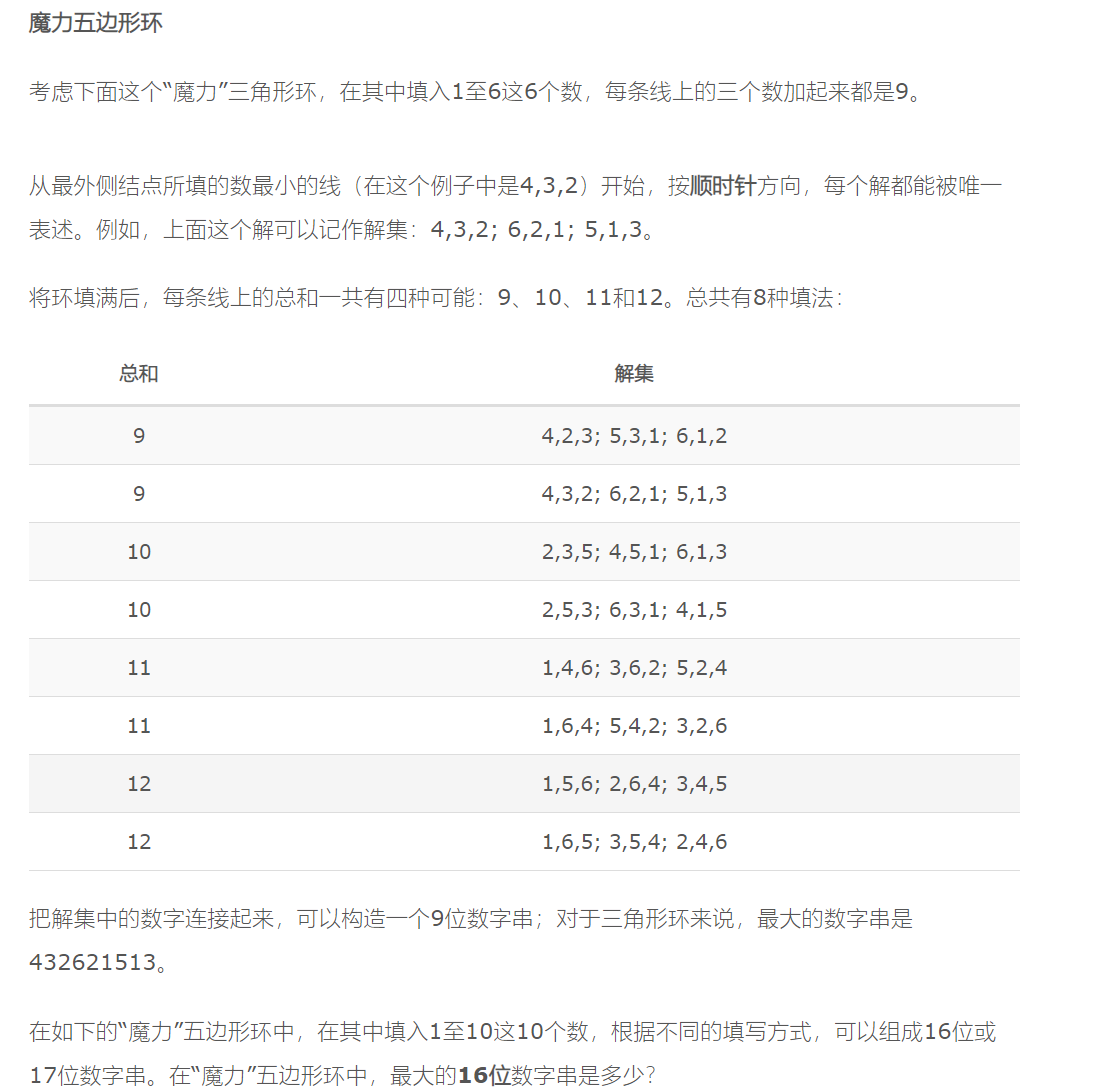
全排列枚举,保证第一个最小,10不会被用到两次,然后计算即可
#include<bits/stdc++.h> using namespace std; long long ans; int a[101]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int main(){ for(int i=1;i<=10;i++) a[i]=i; do{ if(min(a[1],min(a[4],min(a[6],min(a[8],a[10]))))!=a[1])continue; if(a[2]==10||a[3]==10||a[5]==10||a[7]==10||a[9]==10)continue; int temp=a[1]+a[2]+a[3]; if(a[4]+a[3]+a[5]!=temp)continue; if(a[6]+a[5]+a[7]!=temp)continue; if(a[8]+a[7]+a[9]!=temp)continue; if(a[10]+a[9]+a[2]!=temp)continue; long long res=0; if(a[1]==10)res*=10; res=res*10; res+=a[1]; if(a[2]==10)res*=10; res=res*10; res+=a[2]; if(a[3]==10)res*=10; res=res*10; res+=a[3]; if(a[4]==10)res*=10; res=res*10; res+=a[4]; if(a[3]==10)res*=10; res=res*10; res+=a[3]; if(a[5]==10)res*=10; res=res*10; res+=a[5]; if(a[6]==10)res*=10; res=res*10; res+=a[6]; if(a[5]==10)res*=10; res=res*10; res+=a[5]; if(a[7]==10)res*=10; res=res*10; res+=a[7]; if(a[8]==10)res*=10; res=res*10; res+=a[8]; if(a[7]==10)res*=10; res=res*10; res+=a[7]; if(a[9]==10)res*=10; res=res*10; res+=a[9]; if(a[10]==10)res*=10; res=res*10; res+=a[10]; if(a[9]==10)res*=10; res=res*10; res+=a[9]; if(a[2]==10)res*=10; res=res*10; res+=a[2]; ans=max(ans,res); }while(next_permutation(a+1,a+1+10)); cout<<ans; return 0; }
Problem 69
Totient maximum
就是裸的筛欧拉函数
#include<bits/stdc++.h> using namespace std; const int N=1000010; int n,id,len; double ans=2; int phi[N]; bool v[N]; int p[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void get_phi(){ phi[1]=1; for(int i=2;i<=n;i++){ if(!v[i]){ p[++len]=i; phi[i]=i-1; } for(int j=1;j<=len&&p[j]*i<=n;j++){ v[p[j]*i]=1; if(i%p[j]==0){ phi[p[j]*i]=p[j]*phi[i]; break; } phi[p[j]*i]=phi[i]*phi[p[j]]; } if((double)phi[i]/i<ans)ans=(double)phi[i]/i,id=i; } } int main(){ n=read(); get_phi(); cout<<id; return 0; }
Problem 70
Totient permutation
改一下加一个判断即可
#include<bits/stdc++.h> #define int long long using namespace std; const int N=10000010; int n,id,len; double ans=0; int phi[N]; bool v[N]; int p[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void get_phi(){ phi[1]=1; for(int i=2;i<=n;i++){ if(!v[i]){ p[++len]=i; phi[i]=i-1; } for(int j=1;j<=len&&p[j]*i<=n;j++){ v[p[j]*i]=1; if(i%p[j]==0){ phi[p[j]*i]=p[j]*phi[i]; break; } phi[p[j]*i]=phi[i]*phi[p[j]]; } int x=i; int f=0,ff=0; while(x){ f+=pow(10,x%10); x/=10; } x=phi[i]; while(x){ ff+=pow(10,x%10); x/=10; } if(f==ff){ if((double)phi[i]/i>ans)ans=(double)phi[i]/i,id=i; } } } signed main(){ n=read(); get_phi(); cout<<id; return 0; }
Problem 71
Ordered fractions
首先我介绍一种树叫做SB树(Stern-Brocot 树)
他是专门处理这种真分数的,想了解的可以去OIwiki上面看(点上面
可知每一层下来我们都会得到一个序列,这个序列都是真分数并且递增,那不就好做了吗
我们先找到第一次出现的$\frac{3}{7}$然后找到它左边的那个分数,可知它们两个相加的值是介于它们之间的,我们只需要继续做下去知道不合法即可
#include<bits/stdc++.h> using namespace std; int main(){ int a=2,b=5; while(b+7<=1000000){ a+=3,b+=7; } cout<<a; return 0; }
Problem 72
Counting fractions
最简真分数,就是求phi然后加起来就行了,注意1不能加上
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1000010; int n,id,len; long long ans; int phi[N]; bool v[N]; int p[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline void get_phi(){ phi[1]=1; for(int i=2;i<=n;i++){ if(!v[i]){ p[++len]=i; phi[i]=i-1; } for(int j=1;j<=len&&p[j]*i<=n;j++){ v[p[j]*i]=1; if(i%p[j]==0){ phi[p[j]*i]=p[j]*phi[i]; break; } phi[p[j]*i]=phi[i]*phi[p[j]]; } ans+=phi[i]; } } signed main(){ n=read(); get_phi(); cout<<ans; return 0; }
Problem 73
Counting fractions in a range
还是熟悉的SBtree,只需要初始时候把左边和右边分别改成$\frac{1}{2}$和$\frac{1}{3}$即可,然后求解
#include<bits/stdc++.h> using namespace std; int build(int a,int b,int c,int d){ int x=a+c; int y=b+d; int res=0; if(y<=12000){ res+=build(a,b,x,y); res+=build(x,y,c,d); res++; } return res; } int main(){ printf("%d",build(1,2,1,3)); return 0; }
Problem 74
Digit factorial chains
没啥技术性的,暴力搜索就完事了
#include<bits/stdc++.h> #define int long long using namespace std; int fac[1001]; int answer; map<int,int>mp; int check(int x,int d){ if(mp[x]) return d-1; mp[x]=d; int res=0; while(x){ res+=fac[x%10]; x/=10; } return check(res,d+1); } signed main(){ int n; scanf("%d",&n); fac[0]=1; for(int i=1;i<=9;i++) fac[i]=fac[i-1]*i; for(int i=1;i<=n;i++){ int ans=check(i,1); if(ans==60)answer++; mp.clear(); } cout<<answer; return 0; }
Problem 75
Singular integer right triangles
首先引出勾股数,最经典的就是$3,4,5$这一组了
勾股数组(也是毕达哥拉斯三元组)是指$a^2+b^2+c^2$且$a,b,c$均为正整数的解,可以证明,有无穷个勾股数组
因为一旦有一组解,我们可以乘上系数得到其他解,所以就有本源勾股数组(简称PPT),它是指不能通过其他勾股数组得到的勾股数组
那我们考虑怎么求出每一组本源勾股数组,从而求出范围内所有勾股数组
首先我列出几个勾股数组
$(3,4,5),(5,12,13),(7,24,25)$
发现规律没有,前两个数总是一奇一偶,这是巧合吗?
假设$a,b$都是奇数,那么$c$肯定是偶数,但是通过$\frac{a^2+b^2}{2}$和$\frac{c^2}{2}$可以得出,这是不成立的
假设$a,b$都是偶数,那么$c$也是偶数,并不是本源勾股数组了
那么如何找本源勾股数组呢?
我们先假设$a$是奇数,$b$是偶数,$c$是奇数
$a^2+b^2=c^2$
$a^2=c^2-b^2$
$a^2=(c-b)(c+b)$
首先,$(c-b)$和$(c+b)$是互质的,证明如下
假设$d|(c-b)$并且$d|(c+b)$
那么就有$d|(c-b+c+b),d|(2c)$
$d|(c+b-c+b),d|(2b)$
$d^2|(c-b)(c+b),d^2|a^2,d|a$
所以$d$不可能整除2,所以$d|c,d|b$
因为$gcd(a,b,c)=1$所以$d$只可能为1
证毕
然后考虑对$a^2$进行质因数分解,分成$(c+b)(c-b)$
因为互质,所以就是把一种质数分给一个,一种质数分给另一个,然后就是方程求解的时候
设$s^2=(c+b),t^2=(c-b)$
所以$a=st$
$b=\frac{s^2-t^2}{2}$
$c=\frac{s^2+t^2}{2}$
然后就求出来了!
但是我们还要证明我们求出来的是本源勾股数组,即$gcd(a,b,c)=1$
还是反证法,假设有公因数$p$,不难发现一定只会被$s$和$t$其中一个整除,不然就不互质了
然后搞一搞就得出$b\mod p$≠$0$剩下的也是一样的
#include<bits/stdc++.h> #define int long long using namespace std; int ans; int cnt[1500010]; signed main(){ int N; // scanf("%lld",&N); N=1500000; for(int s=1;;s+=2){ if(s>N)break; for(int t=1;t<s;t+=2){ int a=s*t,b=(s*s-t*t)/2,c=(s*s+t*t)/2; if(a>N||b>N||c>N)break;; if(a+b+c>N)continue; if(__gcd(s,t)>1)continue; int tot=a+b+c; for(int i=tot;i<=N;i+=tot) cnt[i]++; } } for(int i=1;i<=N;i++) if(cnt[i]==1)ans++; cout<<ans; return 0; }
Problem 76
Counting summations

完全背包搞一搞,注意分成两个
#include<bits/stdc++.h> #define int long long using namespace std; const int N=110; int n; int dp[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ dp[0]=1; n=read(); for(int i=1;i<n;i++) for(int j=i;j<=n;j++) dp[j]+=dp[j-i]; cout<<dp[n]; return 0; }
Problem 77
Prime summations

欧拉筛然后背包搞一搞
#include<bits/stdc++.h> #define int long long using namespace std; const int N=10000010; int n,len,ans=1e9; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int p[N],v[N]; int dp[N]; inline void get_prime(){ for(int i=2;i<=n;i++){ if(!v[i]){ p[++len]=i; for(int j=i;j<=n;j++){ dp[j]+=dp[j-i]; if(dp[j]>5000){ ans=min(ans,j); } } } for(int j=1;j<=len&&p[j]*i<=n;j++){ v[p[j]*i]=1; if(i%p[j]==0)break; } } } signed main(){ dp[0]=1; n=read(); get_prime(); cout<<ans; return 0; }
Problem 78
Coin partitions

一样的背包,但是取个余,因为答案可能很大
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1010000; int n,ans=1e9; int dp[N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ dp[0]=1; n=read(); for(register int i=1;i<n;i++){ for(register int j=i;j<=n;j++){ dp[j]+=dp[j-i]; dp[j]%=1000000; } for(register int j=1;j<=i;j++) if(dp[j]%1000000==0){ ans=j; break; } } cout<<ans; return 0; }
Problem 79
Passcode derivation

方法一:肉眼看出 73162890
方法二:参考方法一
#include<bits/stdc++.h> using namespace std; int n=9; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } bool nt[11][11]; bool pre[11][11]; int main(){ for(int i=1;i<=50;i++){ int a; cin>>a; int b=a/10%10,c=a%10; a/=100; pre[b][a]=pre[c][a]=pre[c][b]=1; nt[a][b]=nt[b][c]=nt[a][c]=1; } for(int i=0;i<=9;i++){ printf("\n在%d之前的数:",i); for(int j=0;j<=9;j++) if(pre[i][j])printf("%d ",j); printf("\n在%d之后的数:",i); for(int j=0;j<=9;j++) if(nt[i][j])printf("%d ",j); } return 0; }
Problem 80
Square root digital expansion

首先可以考虑夹逼法,也就是不断增大,直到再+1就超过了,就继续做下一位
但是这样的话每次都要做高精度乘法,很麻烦,时间复杂度也挺高,但是思维难度不高,所以在此我介绍另一种方法
如果求$\sqrt{n}$,我们令$a=5n,b=5$
当$a>=b$时
$a=a-b$
$b=b+10$
否则
$a*=100$
$b=b/10*100+5$也就是在最后一位前面插入$0$,但是最后一位一定要保证是$5$
最后计算的时候不能计算最后两位,就行了
这个的优点就是不用很麻烦的乘法,简单加减就行了,必要的时候适合手算模拟
code:(高精度遭不住)
#include<bits/stdc++.h> using namespace std; int ans; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } inline bool check(int x){ return (int)sqrt(x)*(int)sqrt(x)==x; } struct Bigint{ int a[1010]; int len; Bigint(){ memset(a,0,sizeof a); } Bigint operator+(const Bigint &x){ Bigint c; for(int i=1;i<=200;i++) c.a[i]=a[i]+x.a[i]; for(int i=1;i<=200;i++){ c.a[i+1]+=c.a[i]/10,c.a[i]%=10; if(c.a[i])c.len=i; } return c; } Bigint operator-(const Bigint &x){ Bigint c; for(int i=1;i<=200;i++){ c.a[i]+=a[i]-x.a[i]; if(c.a[i]<0)c.a[i]+=10,c.a[i+1]--; } for(int i=1;i<=200;i++){ c.a[i+1]+=c.a[i]/10; c.a[i]%=10; if(c.a[i])c.len=i; } return c; } void change(int x){ len=(int)log10(x)+1; for(int i=1;i<=200;i++){ a[i]=x%10; x/=10; } return; } Bigint operator*(const int &x){ Bigint c; for(int i=1;i<=200;i++) c.a[i]=a[i]*x; for(int i=1;i<=200;i++){ c.a[i+1]+=c.a[i]/10,c.a[i]%=10; if(c.a[i])c.len=i; } return c; } bool operator>=(const Bigint &x){ for(int i=200;i>=1;i--){ if(a[i]>x.a[i])return true; if(a[i]<x.a[i])return false; } return true; } inline void prepare(){ for(int i=1;i<=200;i++){ a[i+1]+=a[i]/10; a[i]%=10; if(a[i])len=i; } return ; } }; inline void sqrt_(int n,int digits){ int last=digits+1; Bigint a,b; a.change(5*n); b.change(5); while(b.len<=last){ if(a>=b){ a=a-b; b.a[2]++; b.prepare(); }else{ a=a*100; b.a[1]=0; b=b*10; b.a[1]=5; } a.prepare(); b.prepare(); } for(int i=102;i>=3;i--) ans+=b.a[i]; } int main(){ int n=read(); for(int i=1;i<=n;i++){ if(check(i))continue; sqrt_(i,100); } cout<<ans; return 0; }
Problem 81
Path sum: two ways
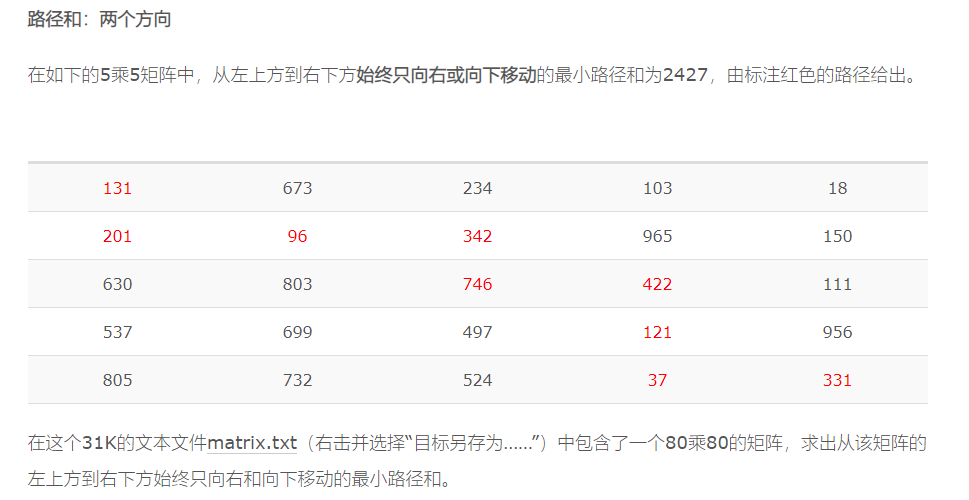
典型的方格取数最简单的,$dp[i][j]=min(dp[i-1][j],dp[i][j-1])+a[i][j]$
#include<bits/stdc++.h> using namespace std; int n=80; int dp[81][81]; int a[81][81]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } int main(){ memset(dp,0x3f,sizeof dp); dp[1][0]=dp[0][1]=dp[0][0]=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){ a[i][j]=read(); dp[i][j]=min(dp[i-1][j],dp[i][j-1])+a[i][j]; } cout<<dp[n][n]; return 0; }
Problem 82
Path sum: three ways
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1009; const int inf=1e15; int n,m; int a[N][N]; int dp[N][N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } signed main(){ n=80,m=80; for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) dp[i][j]=inf; for(int i=1;i<=n;i++) dp[i][0]=0; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read(); for(int j=1;j<=m;j++){ int res=inf; for(int i=1;i<=n;i++){ res=min(res,dp[i][j-1])+a[i][j]; dp[i][j]=min(dp[i][j],res); } res=inf; for(int i=n;i>=1;i--){ res=min(res,dp[i][j-1])+a[i][j]; dp[i][j]=min(dp[i][j],res); } } int ans=inf; for(int i=1;i<=n;i++) ans=min(ans,dp[i][m]); printf("%lld",ans); return 0; }
Problem 83
Path sum: four ways
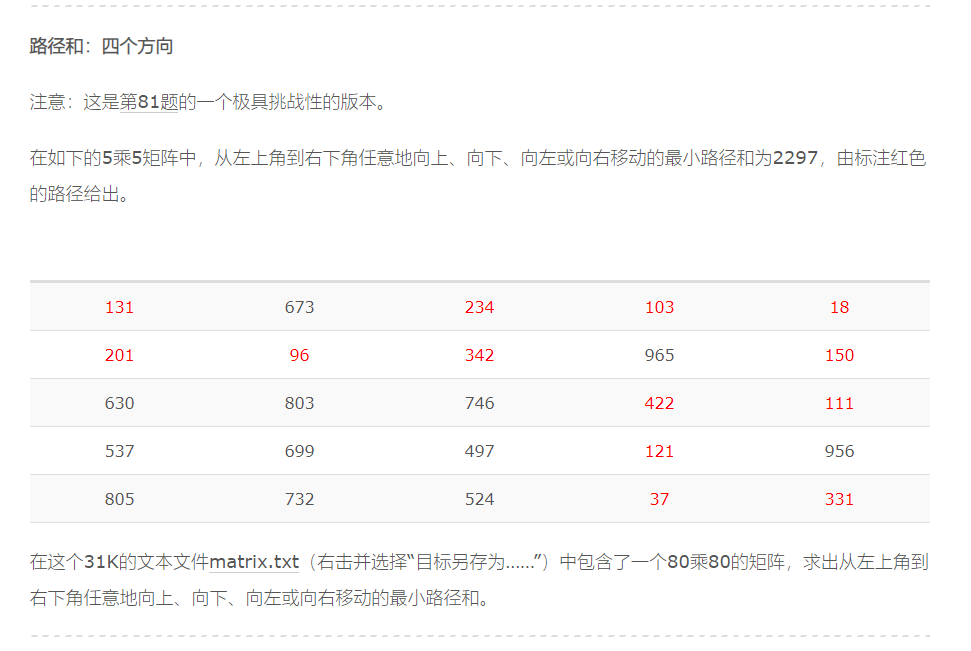
就当作图来跑一遍就可以了,dij走起
#include<bits/stdc++.h> #define mk(x,y) (node){x,y} using namespace std; const int N=1001; int n=80,m=80,cnt; int v[N*N]; int last[N*N]; int dis[N*N]; inline int read(){ int f=1,x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return f*x; } struct node{ int x,v; bool operator<(const node &b)const{ return v>b.v; } }; struct edge{ int pre,to; }e[N*N*4]; void add(int x,int y){ cnt++; e[cnt].pre=last[x]; e[cnt].to=y; last[x]=cnt; return; } void dij(){ priority_queue<node>q; q.push(mk(1,v[1])); dis[1]=v[1]; while(!q.empty()){ node h=q.top(); q.pop(); if(h.v>dis[h.x])continue; for(int i=last[h.x];i;i=e[i].pre){ int to=e[i].to; if(dis[h.x]+v[to]<dis[to]){ dis[to]=dis[h.x]+v[to]; q.push(mk(to,dis[to])); } } } printf("%d",dis[n*m]); } int main(){ memset(v,0x3f,sizeof v); memset(dis,0x3f,sizeof dis); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ int now=(i-1)*m+j; v[now]=read(); if(i>1)add((i-2)*m+j,now),add(now,(i-2)*m+j); if(i<n)add(i*m+j,now),add(now,i*m+j); if(j>1)add((i-1)*m+j-1,now),add(now,(i-1)*m+j-1); if(j<n)add((i-1)*m+j+1,now),add(now,(i-1)*m+j+1); } dij(); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号