【Manacher(马拉车)算法】
Manacher
英译过来就是马拉车
是一个求一个字符串中最长回文连续子序列的算法
例如abaabaabb最长的就是7
abaaaaba最长就是8
ababbb最长就是3
注意:一个字符串可能不只有一个最长回文连续子序列
传统做法就是枚举中间点向两边扩展,时间复杂度是O(N^2)
然后这个算法就优化到了O(N)
这是优化吗,性质都变了啊喂
算法实现
首先回文分为两种:奇回文和偶回文如果枚举的话,有时候是字符,有时候要枚举字符之间的位置,就很麻烦
为了操作方便(因为我们要定义以i为中心),我们把它们都变成奇回文
怎么做呢?很简单,全部插入一个符号即可(没出现过)
例如
abaababa ——> (#a#b#a#a#b#a#b#a#)
前后是防止越界,你可以随便定义(只要字符串里没有的,不会冲突)
原来aba就可以变成#a#b#a#
原来baab就可以变成#b#a#a#b#
这样一来就全部变成了奇回文啦!
我们定义P[i]是以i为中心的,最长回文串的半径(包括自己)
| 字符串 | ( | # | a | # | b | # | a | # | a | # | b | # | a | # | b | # | a | # | ) |
| P | 1 | 1 | 2 | 1 | 4 | 1 | 2 | 7 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 1 |
我们现在要做的就是O(N)处理出每一个P[i]
考虑能不能根据之前已经得到的来推测出答案呢
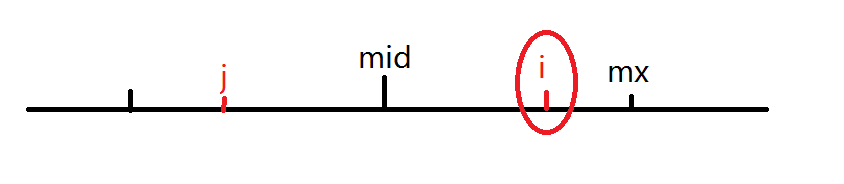
当前我们枚举到i,已知有一个以mid为中心的回文子串,其右端点到了mx
可知以mid为分界线,左右两边是完全对称的(回文子串定义)
当i+p[j]<mx时

我们就可以直接更新答案,因为不可能更长了
当i+p[j]>=mx时
我们只能到mx这个位置,因为我们不知道mx后面是否还能继续匹配
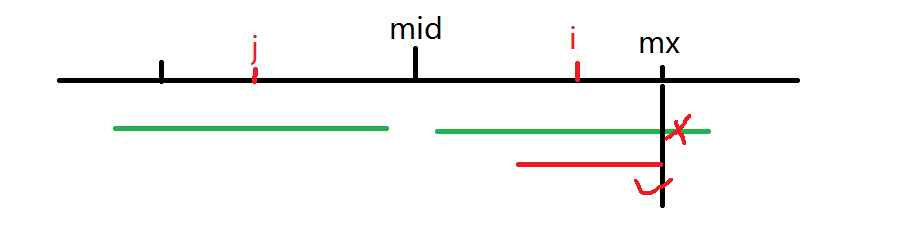
(只取红色部分)
我们就可以根据i的对称点j来更新答案,但是p[i]不一定等于p[j],因为mx后面的还是未知的,我们不知道,这一部分暴力匹配就是了
可知mx是一直在增大,每增大一次,我们需要比较一次,mx最多从0到n,所以也就是O(N)的复杂度
其实和KMP都有一个运用已知答案的思想
最后输出答案的时候我们半径减一即可(可以自己手%一下找找规律)
【模板】manacher算法
1 #include<bits/stdc++.h> 2 using namespace std; 3 char s_new[21000002]; 4 char s[11000002]; 5 int p[21000002]; 6 int INIT(){//转换字符串 7 int len=strlen(s); 8 s_new[0]='$'; 9 s_new[1]='#'; 10 int j=2; 11 for(int i=0;i<len;i++) 12 { 13 s_new[j++]=s[i]; 14 s_new[j++]='#'; 15 } 16 s_new[j]='\0'; 17 return j; 18 } 19 int manacher() 20 { 21 int len=INIT(); 22 int ans=-1; 23 int id;//中心 24 int mx=0;//能达到的已知的右端点 25 for(int i=1;i<=len;i++) 26 { 27 if(i<mx) 28 p[i]=min(p[2*id-i],mx-i);//更新取较小的一个 29 while(s_new[i+p[i]]==s_new[i-p[i]])//暴力扩展 30 p[i]++; 31 if(mx<i+p[i])//更新mx 32 { 33 id=i, 34 mx=p[i]+i; 35 } 36 ans=max(ans,p[i]-1);//更新答案 37 38 } 39 return ans; 40 } 41 int main() 42 { 43 scanf("%s",s); 44 cout<<manacher(); 45 return 0; 46 }

