【AC自动机（有了这个我就能AC了吗）】

前置芝士：Trie    KMP

概念

AC自动机，其实叫做前缀树，至于为什么叫做AC自动机（陷入沉思.......）应该是和它的作用有关。他是典型的多模匹配算法，也就是多个模式串和一个文本串（KMP是一对一辅导）

操作

其实和普通的trie差不多，还是先建Trie，但是因为这个和KMP有着重要的关系，所以我们匹配的时候也会利用一个回退的指针，从而保证在O（N），对，和next的差不多

 

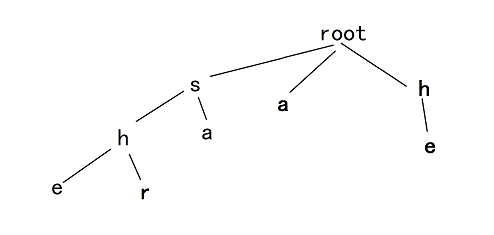
 假设我们现在有这么一颗Trie

AC自动机的精妙之处就是当匹配失败时，我们会有一个fail指针保证跳到的地方可以接着匹配

而fail指针怎么确定呢？因为我们要保证可以接着匹配，所以我们要保证现在跳到的地方到根节点这一串是当前这一串的后缀，可能有点复杂

我们先把fail指针画出来

 

 

 

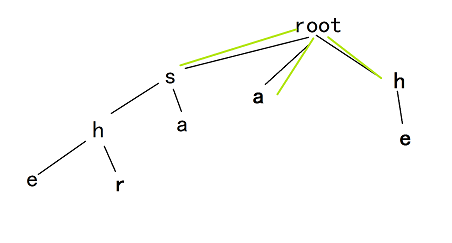
 因为我们跳到的地方是当前已经匹配的后缀，所以需要运用到前面的已经确定的fail指针，所以第一层就是全部指向根节点

 for(int i=0;i<26;i++)
        {
            int to=ch[0][i];
            if(to)
                q.push(to);
        }

然后就是愉快的BFS（广度优先搜索）

到了第二层，我们这个点就和他的父亲的fail指针的同样的儿子做比较，是不是很绕

一直当前root->fail[u]是root->u的最长后缀，我们要加进来，就看他们的下一位是不是相同，可以理解吧（其实就和KMP的操作一样）

但是由于下一个节点不唯一，所以我们就找同位置的儿子，因为有的话就接上去了，然后更新

但是万一没有下一个节点，由于我们想要一直搜索到底，所以我们就跳fail指针

 for(int i=0;i<26;i++)
            {
                int to=ch[u][i];
                if(to)
                {
                    fail[to]=ch[fail[u]][i];
                    q.push(to);
                }
                else
                    ch[u][i]=ch[fail[u]][i];
            }

 

 

 

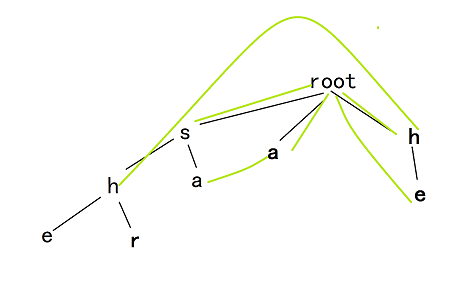
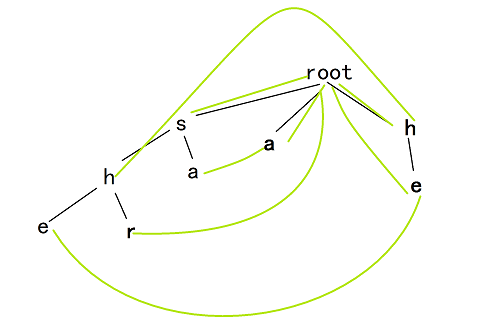
 这就是get_fail的操作了

void get_fail()
    {
        queue<int>q;
        for(int i=0;i<26;i++)
        {
            int to=ch[0][i];
            if(to)
                q.push(to);
        }
        while(!q.empty())
        {
            int u=q.front();
            q.pop();
            for(int i=0;i<26;i++)
            {
                int to=ch[u][i];
                if(to)
                {
                    fail[to]=ch[fail[u]][i];
                    q.push(to);
                }
                else
                    ch[u][i]=ch[fail[u]][i];
            }
        }
    }

接下来就是查找了，因为我们前面已经帮他跳fail，所以一直搜索就完了（奥利给！）

但是因为搜索到这个点后，有多个fail指针可以回退，万一其中可能是某个串的结尾，所以我们需要循环

int find(string s)
    {
        int u=0,ans=0;
        for(int i=0;i<s.size();i++)
        {
            u=ch[u][get(s[i])];
            for(int k=u;k&&val[k]!=-1;k=fail[k])
            {
                ans+=val[k];
                val[k]=-1;
            }
        }
        return ans;
    }

以上就是最基本的操作了，其实那些题的话，只需要改一些操作，例如辅助数组或者val，都是可以变通的，但是下面这个需要单独讲讲

二次加强的

我们都知道，如果每次到一个点都要遍历fail点，会很耗费时间，因为搜索到一个点，顺着他fail指针的这条线上的都会遍历，所以我们每次都只需要将第一个点搜索过的次数++，然后最后统一处理遍历就可以了

但是这样又有一个问题，一个点可能有多个儿子，意思是他会继承多个儿子的ans值，而我们需要等到这个点继承完了所有的儿子点才能把他的给他的fail指针，

熟不熟悉，就是topu排序，等到儿子继承完了再向上传递

所以我们在建立fail指针的时候，入度数组要++

 int to=ch[u][i];
                if(to)
                {
                    fail[to]=ch[fail[u]][i];
                    rd[ch[fail[u]][i]]++;
                    q.push(to);
                }

找的时候我们找到第一个就行，消除遍历

  void find(char s[])
    {
        int u=0;
        for(int i=0;s[i];i++)
        {
            u=ch[u][get(s[i])];
            val[u]++;
        }
        topu();
         for(int i=1;i<=n;i++)
             printf("%d\n",val[a[i]]);
    }

但是需要topu排序来向上传递

void topu()
    {
        queue<int>q;
        for(int i=1;i<sz;++i)
            if(rd[i]==0)q.push(i);            
        while(!q.empty())
        {
            int u=q.front();
            q.pop();
            int v=fail[u];
            rd[v]--;     
            val[v]+=val[u];     
            if(rd[v]==0)q.push(v);   
        }
    }

最后就OK了

棒！