【扩展KMP(Z函数)(这个区间看着不是很爽)】
前面已经介绍了经典的烤馍片(KMP)算法,所以我们继续来介绍扩展KMP
算法目的
我们首先要明白这个是求什么的。给定两个字符串S和T(长度分别为n和m),下标从0开始,定义extend[i]等于S[i]...S[n-1]与T的最长相同前缀的长度,求出所有的extend[i]。看不懂没关系,来一发样例
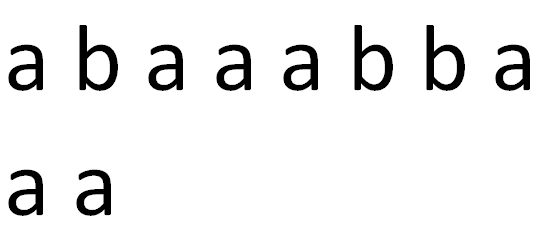
我们先对齐,然后求最长公共前缀,这里就是1然后把t串向后移
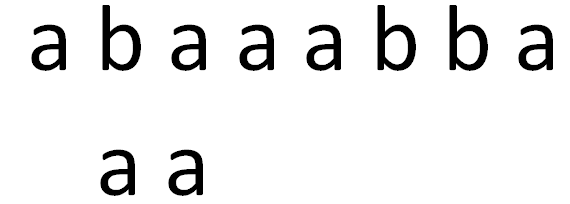
这里就是0,然后一直重复操作,把t串向后移,然后比较。当然,我们这样暴力最坏是可以O(N^2)的
那为什么叫做扩展KMP呢?因为我们这个当extend[i]=m时,就证明在S这个串里有t串,并且算法操作和KMP有异曲同工之妙。
算法思想
(因为我数组都喜欢以一为下标,所以,下文都是的)
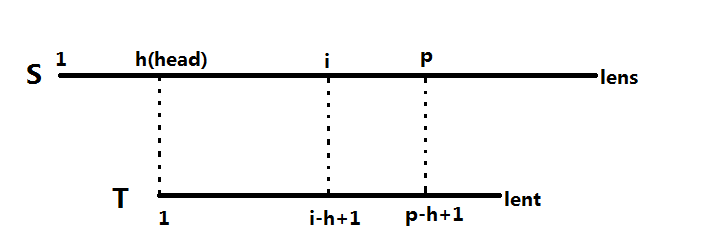
我们假装现在已经匹配到第i个点,h是T串的第一位所对应的位置,p是已经匹配成功的下一个点。
我们需要一个辅助数组next,(当然这个和KMP的不一样)next[i]含义为:T[i]...T[m - 1]与T的最长相同前缀长度,m为串T的长度下面来个小小例子
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| T | a | a | a | b | a | b | a |
| next[i] | 7 | 2 | 1 | 0 | 1 | 0 | 1 |
说白了就是从第i位开始,把包括他后面的复制出来,两个串来找最长公共前缀和
好了,回到刚才的来,我们按照暴力就会把T串的第一个移过来,重新开始匹配,但是KMP最擅长的就是利用前面的已知信息了!
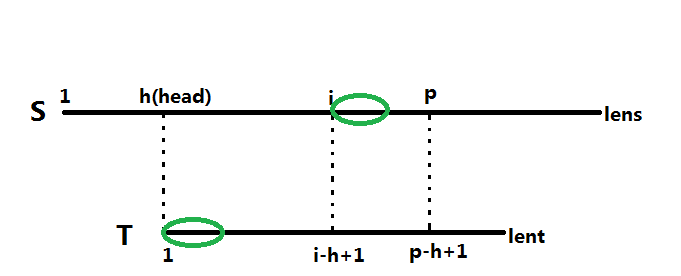
所以我们的主要目的就是能找到两个上面圈圈的地方相等,这样就能节省很多时间。但是我们怎么匹配呢?
现在已知S[i.p)=T[i-h+1,p-h+1)而这个我们之前已经做过了next操作,(也就是从i-h+1开始,后面的复制下来和原串比较)现在比较情况有如下三种
1.i+next[i-h+1]<p

由next数组得到,区间1=区间2,因为p以前的都是匹配成功的,所以区间3=区间2。所以我们就继承了,但是会不会存在T[j]=S[k]呢?也就是继承后还可以继续匹配。别急
假设成立,因为S[k]=T[l],所以T[j]=T[l],所以next数组应该还要大,大到包括他们,所以不成立,所以这个时候的extend[i]=next[i-h+1]
2.i+next[i-h+1]=p
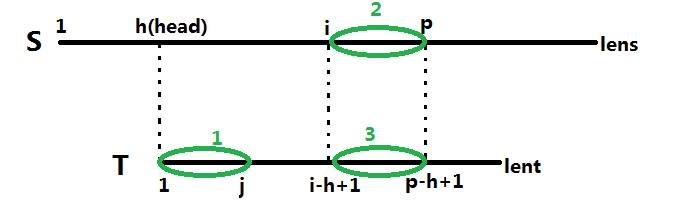
所以上面的三个区间都是相同的,但是由于p后面的我们不知道,所以我们这个时候继承完了可以从p和j开始继续向后搜索,直到不想等。因为这个时候p更新了,所以S[i.p)和T[i-h+1,p-h+1)不再相等(因为相等了前面p也会向后移动)所以我们就需要把j移动到i这个地方,才能保证区间内的相等
所以extend[i]=p-i(没有+1是因为p本来也是比右端点多一,而减i正好抵消)
3.i+next[i-h+1]>p
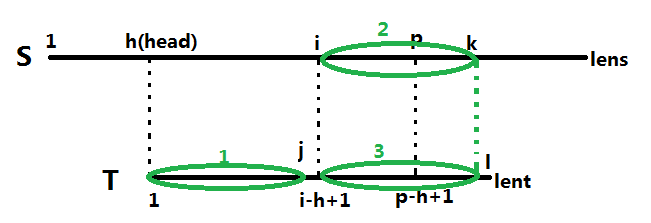
超出了亿点点
由图得,区间1=区间3,但是区间3不等于区间2(因为p后面的肯定是不相等的),所以盲目的再去比较是没有意义的,所以还是
extend[i]=p-i
算法实现
首先得把next数组求出来把。其实你看看,next和extend的本质是一样的,都是找最长公共前缀,只是next是比较特殊的extend,因为这时候S串=T串。(这就是和KMP操作一样的地方)
来康康代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=20000010; 4 char s[N],t[N]; 5 int nt[N],ntend[N]; 6 int lens,lent; 7 void getnext() 8 { 9 int h=1,p=1; 10 nt[1]=lent;//因为自己和自己的最长公共前缀就是自己本身的长度 11 for(int i=2;i<=lent;i++) 12 { 13 if(i>=p||i+nt[i-h+1]>=p) 14 { 15 if(i>=p)p=i;//对于i>=p,就是两个串没有任何地方相等,就向后跳 16 while(p<=lent&&t[p]==t[p-i+1])p++;//匹配(因为大于的情况肯定匹配不到,所以这主要是针对于等于的情况) 17 nt[i]=p-i;//记录(因为两个的都是一样的) 18 h=i;//更新, 19 } 20 else nt[i]=nt[i-h+1];//小于的情况 21 } 22 } 23 void kmp() 24 { 25 int h=1,p=1; 26 for(int i=1;i<=lens;i++) 27 { 28 if(i>=p||i+nt[i-h+1]>=p) 29 { 30 if(i>=p)p=i; 31 while(p<=lens&&p-i<=lent&&s[p]==t[p-i+1])p++;//这里一定要多一个p-i<=lent,因为这里是判断长度不能超过T串的 32 ntend[i]=p-i; 33 h=i; 34 } 35 else ntend[i]=nt[i-h+1]; 36 } 37 } 38 int main() 39 { 40 scanf("%s%s",s+1,t+1);//从1开始存储 41 lens=strlen(s+1); 42 lent=strlen(t+1); 43 getnext();//匹配自己,初始化next数组 44 kmp();//匹配 45 long long ans=0; 46 for(int i=1;i<=lent;i++) 47 ans^=(long long)i*(nt[i]+1); 48 cout<<ans<<endl; 49 ans=0; 50 for(int i=1;i<=lens;i++) 51 ans^=(long long)i*(ntend[i]+1); 52 cout<<ans; 53 return 0; 54 }

