【KMP算法(烤馍片,真香)】
KMP
KMP算法,又称烤馍片算法,是字符串匹配的改良算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
我们就在一步一步的实践探索中来理解这个神奇的算法吧
说到字符串匹配,就是给你两个串,看一个文本串里是否含有一个模式串(文本串为root,模式串为s)
暴力算法
暴力算法我们都会,一位一位的比较嘛,不一样向后移动就行了
下面是一个例子
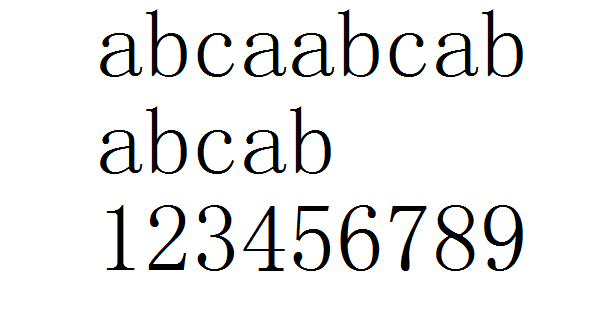
我们拿到这个串的时候,就先让s[1]和root[1]对齐(下标从1开始)
当前四位都匹配成功的时候(abca)我们匹配第五位,第五位不匹配,按照暴力的算法我们就会让s[1]和root[2]对齐
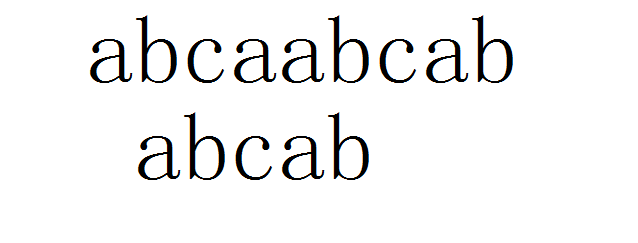
这样的话roo里面的指针就会回退,这是对已知信息的极大的浪费,
我们有没有一种方法能利用已匹配的信息让root的指针不回退,从而让s(模式串)直接移动到我们想要的位置呢?
答案是有的,那就是烤馍片算法
KMP算法
如何操作
我们再拿样例来分析一下
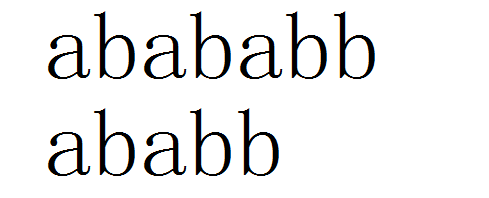
我们匹配好前面四位的时候,发现第五位不对,我们就移动模式串
根据前面已知的,我们就可以像下面这样
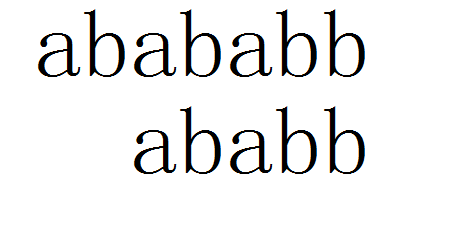
直接向后移动两位,然后我们的roo指针继续从第五位开始,直到匹配成功
这里有一个前缀串和后缀串的知识
如abcde
前缀串:a,ab,abc,abcd,abcde
后缀串:e,de,cde,bcde,abcde
我们要求它们除了自己本身的最长公共前后缀
例如这里,除了本身就没有了
现在不懂没关系,接着往下
我们发现,当匹配不成功的时候,我们root指针所指的位置前面都是匹配的
如上面的abab
这里的最长公共前后缀(除了自己)就是ab
所以我们就可以一次性移动两位
但是这样会不会有中间漏掉的情况呢?(下面的......是省略其中的字符)
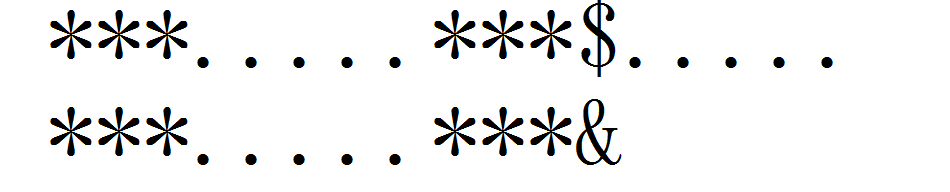
例如这个,我们现在已知匹配了的它除了自己的最长公共前后缀是***
当我们前面的都匹配完了:
![]()
匹配下一位的时候,发现不对,我们就可以直接把模式串开头的下标向后移动到
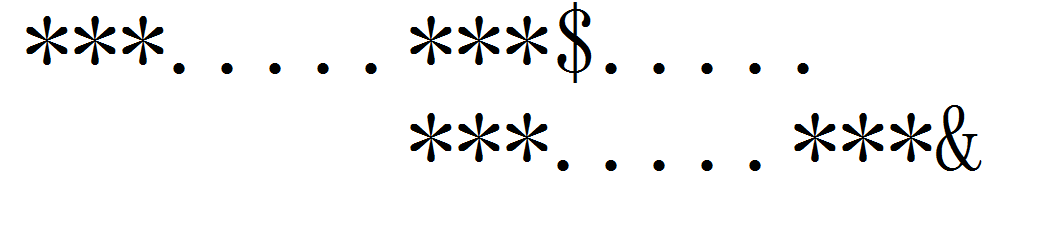
我们假设其中有一种情况
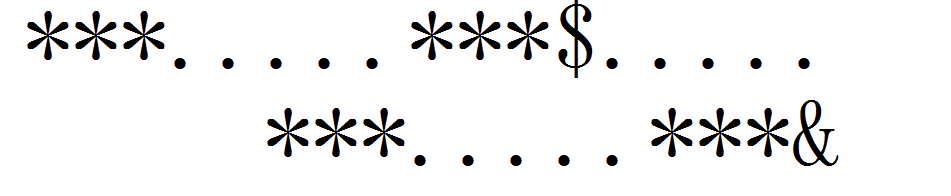
使得这样可以匹配成功(root指针还是在已匹配的那里)

这里就相等
由之前可知
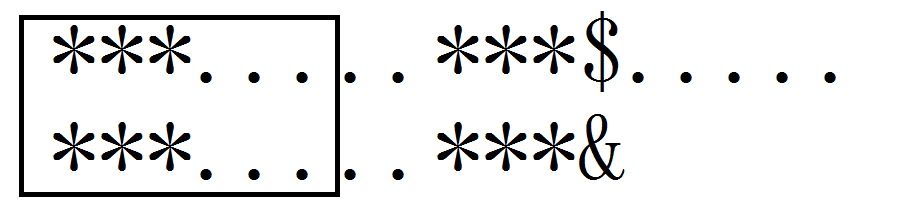
这两个相等
所以最长公共前后缀(除去他自己)就是框起来的玩意儿了,但是我们已知的并不是那个,所以这是矛盾的,所以也就不需要担心上述情况的发生了
通过这里,我们就可以解释一下为什么要除去他自己了,因为我们移动是从最长公共前后缀的前缀移动到后缀,但是如果算上自己的话,相当于没有移动,这就是没有意义的。懂?
我们就可以用一个next数组来存储每一个区间的最长公共前后缀的长度了
再往回看,发现没有,匹配成功的都是模式串的前缀串,所以我们的next数组只需要记录模式串前缀串的最长公共前后缀了
既然理解了KMP的操作方式,我们来看看怎么实现
如何实现
我们next[i]表示模式串1到i的最长公共前后缀的长度
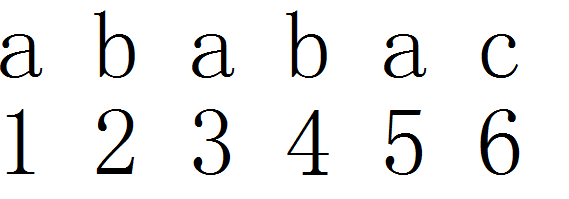
首先next[1]为0(这个很好理解吧,就一个字符,除去自己就没了)
我们再看第二位,我们现在有两个指针,一个i指当前处理的位置,然后一个j表示1---i-1的最长公共前后缀的长度。为什么要j呢?
你想想,我们前面已经匹配好了,如果新加入进来的,也就是i指针所指的,和已知最长的下一位相等,我们不就可以避免重头计算而是很好的利用了

这里i和j的下一位不相等,所以就是
next[2]=j
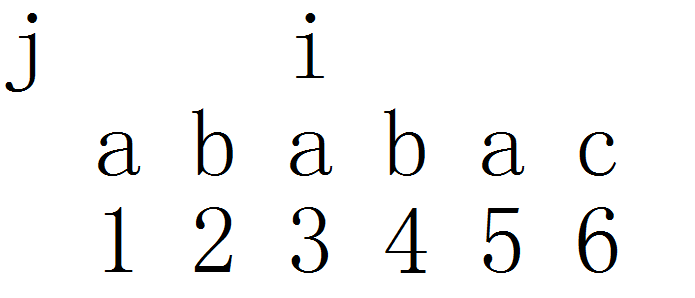
相等
j++
next[i]=j
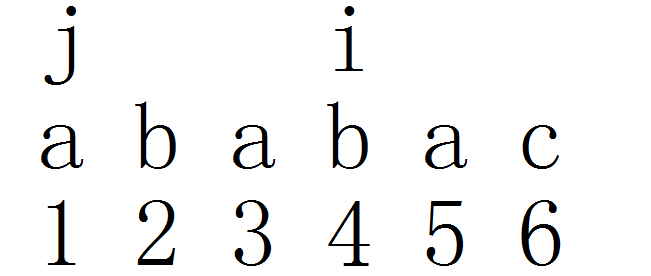
相等
j++
next[i]=j=2

j++
next[i]=j=3

到这里不相等了,意思是我们只能继续寻找比现在长度小的公共前后缀了,但是怎么找呢?
这个例子不明显,我们换一个
![]()
这是已经处理的,现在j等于3,表示当前除了本身的最长公共前后缀长度为3
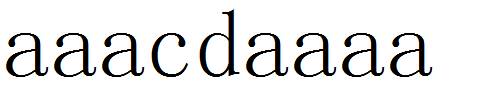
但是这样的话,就不能继续了,我们就要找第二长的公共前后缀了,但是怎么找?
我们来假设一下

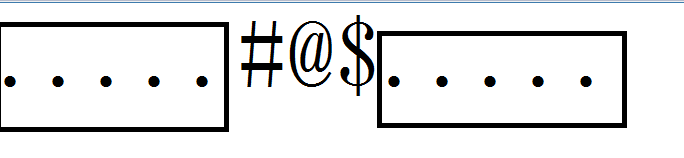
现在这是已知的长度为x
当我们想找到一个长度小于x的时(黄色部分)由于这个的长度小于x并且两个黑框框相等,所以我们就可以合并
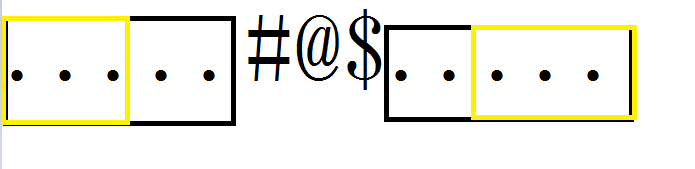
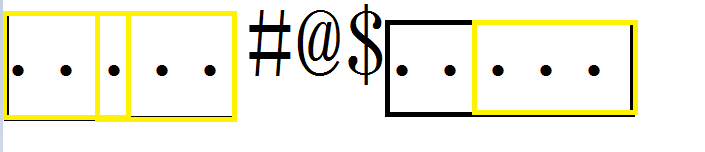
代换过来就是这样,现在就在同一个框框里了,所以我们只需要求next[x]的最长的公共前后缀就行了,懂?不懂得可以私信的,这里是最难的地方
下面就是代码
1 void getnext() 2 { 3 int j=0;//初始为0 4 for(int i=2;i<=n;i++) 5 { //这里就是查找第二长的 回退操作 6 while(j!=0&&s[i]!=s[j+1])j=next[j];//如果j等于0的话,我们直接比较就行了,因为不存在第二长的 7 next[i]=(s[j+1]==s[i]?++j:j);//判断是否相等 8 } 9 return ; 10 }
我们康康全局吧
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1000010; 4 int n; 5 int next[N]; 6 char root[N],s[N]; 7 vector<int> ans; 8 void getnext() 9 { 10 int j=0;//初始为0 11 for(int i=2;i<=n;i++) 12 { //这里就是查找第二长的 回退操作 13 while(j!=0&&s[i]!=s[j+1])j=next[j];//如果j等于0的话,我们直接比较就行了,因为不存在第二长的 14 next[i]=(s[j+1]==s[i]?++j:j);//判断是否相等 15 } 16 return ; 17 } 18 void kmp() 19 { 20 int j=0; 21 int len1=strlen(root+1); 22 int len2=strlen(s+1); 23 for(int i=1;i<=len1;i++) 24 { 25 while(j!=0&&root[i]!=s[j+1]){j=next[j];} 26 if(root[i]==s[j+1])j++;//j是已匹配的长度 27 if(j==len2)ans.push_back(i-len2+1),j=next[j];//长度达到了就记录,但是我们还要继续找, 所以回退 28 } 29 } 30 int main() 31 { 32 scanf("%s%s",root+1,s+1);//输入 33 n=strlen(s+1);//记录长度 34 getnext();//整理next数组 35 kmp();//比较 36 for(int i=0;i<ans.size();i++) 37 printf("%d\n",ans[i]); 38 cout<<next[1]; 39 for(int i=2;i<=n;i++) 40 printf(" %d",next[i]); 41 return 0; 42 }
好的,一份精美的烤馍片就做好了!!!

