【最短路系列问题】
最短路
首先,这玩意儿定义很简单,就是在图上两个点的最短距离叫做两个点的最短路
但恶心的是它的解法多的一p
下面我为大家一一介绍一下这些磨人的小妖精(以下起点都为1,终点都为n)
深度/广度优先搜索(解决单源最短路径)
这个就是利用最基本的搜索,取所有路径的最小值即可
但是它一般求两点之间最短路,效率低
1 #include<bits/stdc++.h> 2 #define inf 99999999 3 using namespace std; 4 int dis[111][111]; 5 bool vis[111]; 6 int n,cnt; 7 void init(int x) 8 { 9 memset(dis,0x3f,sizeof(dis)); 10 for(int i=0;i<=n;i++) 11 { 12 dis[i][i]=0; 13 vis[i]=0; 14 } 15 } 16 void dfs(int x,int w) 17 { 18 if(w>cnt)return;//剪枝,已经不是最短的 19 if(x==n)//到终点 20 { 21 cnt=min(cnt,w); 22 return; 23 } 24 for(int i=1;i<=n;i++) 25 { 26 if(!vis[i]&&dis[x][i]!=inf&&dis[x][i]) 27 { 28 vis[i]=1;//标记 29 dfs(i,w+dis[x][i]);//继续搜 30 vis[i]=0;//取消标记,回溯 31 } 32 } 33 } 34 int main() 35 { 36 int m; 37 scanf("%d%d",&n,&m) 38 int x,y,len; 39 cnt=inf; 40 init(n);//初始化 41 while(m--) 42 { 43 scanf("%d%d%d",&x,&y,&len); 44 dis[x][y]=min(dis[x][y],len);//距离 45 dis[y][x]=dis[x][y]; 46 } 47 vis[1]=1; 48 dfs(1,0); 49 printf("%d\n",cnt); 50 return 0; 51 }
Floyd算法(解决多源最短路径):时间复杂度O(n^3),空间复杂度O(n^2)
纯暴力三重循环,不过暴力一般都用处最多.
思想就是找到要松弛的两个点之间的路径,然后找中间点更新更优值(在第十排):原来有一条i->j的路径,然后我们利用一个中间节点分成两小部分i->k和k->j这也是一种dp的思想
再者注意的就是一定要把中间点的枚举放在最外层,为什么呢,这是根据算法本身决定的。我们不妨来举个例子:
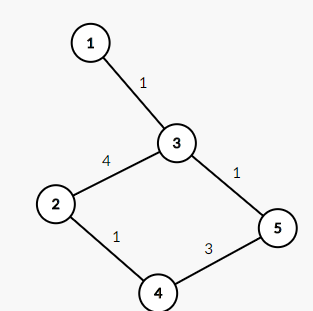
我们现在要1到4的最短路,如果k层循环在最里面,那么dis[1][4]=min(dis[1][4],dis[1][3]+dis[3][4],dis[1][2]+dis[2][4],dis[1][5]+dis[5][4])=MAX(无穷大)
然而这个值就会被定下来,因为我们一次性更新完了,后面也不会再更新了
但是循环在外层的话,每当k做完一次循环,就表明 当前已经是松弛完k这个节点后的最优的结果了,我们松弛完所有节点后答案就出来了
1 #include<bits/stdc++.h> 2 using namespace std; 3 int dst[310][310]; 4 int n,m,t; 5 void floyd() 6 { 7 for(int k=1;k<=n;k++) 8 for(int i=1;i<=n;i++) 9 for(int j=1;j<=n;j++) 10 dst[i][j]=min(dst[i][j],max(dst[i][k],dst[k][j])); 11 } 12 int main() 13 { 14 scanf("%d%d",&n,&m); 15 for(int i=1;i<=m;i++) 16 { 17 int x,y,z; 18 scanf("%d%d%d",&x,&y,&z); 19 dst[x][y]=z; 20 } 21 floyd(); 22 printf("%d",dst[1][n]); 23 return 0; 24 }
Dijkstra算法:不适用于负边权,单源最短路径
这是由于贪心方法实现的,我们首先选取初始点,然后遍历相连的边,记录每个点当前到起点的长度,然后选取距离最小的那个点,确定最短路:
因为当前到这个点的距离已经是最短了,不论其它的哪个点更新过去都会比现在的长,这就是一种贪心的思想。然后我们现在已经确定了两个点的最短路了(起点和刚才选的点)然后再次遍历更新与新加入的这个点相连的点,并更新它们的最短距离,接着重复上述操作再次选取距离最短的点并且没选过......一直做n-1次操作就选完了。
1 #include <bits/stdc++.h> 2 using namespace std; 3 struct node{ 4 int v,w; 5 node(){} 6 node(int vv,int ww) 7 { 8 v=vv; 9 w=ww; 10 } 11 }; 12 vector<node> mp[50001]; 13 int dis[50001];// 表示当前点到源点的最短路径长度 14 int pre[50001];// 记录当前点的前一个结点 15 bool flag[50001];//判断是否已存入该点到集合中 16 int n,m,p; 17 void Djkstra(int u) 18 { 19 flag[u]=1; 20 dis[u]=0; 21 int minid=u,min;//minid是新加入的节点 22 for(int i=2;i<=n;i++)//n-1次操作 23 { 24 for(int j=0;j<mp[minid].size();j++)//遍历相连的边并且更新 25 { 26 27 int V=mp[minid][j].v; 28 int W=mp[minid][j].w; 29 if(!flag[V]&&((W+dis[minid])<dis[V])) 30 { 31 dis[V]=W+dis[minid]; 32 pre[V]=minid; 33 } 34 } 35 minid=0x7fffffff; 36 min=0x7fffffff; 37 for(int j=1;j<=n;j++)//遍历所有点选距离最短的 38 { 39 if(!flag[j]&&dis[j]<min) 40 { 41 min=dis[j]; 42 minid=j; 43 } 44 } 45 if(minid<=n) 46 flag[minid]=1;//打标记 47 } 48 } 49 int main() 50 { 51 52 cin>>n>>m>>p; 53 for(int i=1;i<=n;i++) 54 { 55 dis[i]=2147483647;//初始化 56 } 57 while(m--) 58 { 59 int x,y,z; 60 cin>>x>>y>>z; 61 mp[x].push_back(node(y,z)); 62 } 63 Djkstra(p); 64 cout<<dis[n]; 65 }
但是你去康康洛谷那个加强版的就知道你过不了(太蒟蒻了)
原因就是我们每次都遍历所有的点找距离最小的太麻烦了,分分钟超时
所以我们就有了堆优化
Dijkstra+堆优化:更fast
说是堆优化,其实就是优先队列(因为是用堆实现的)。优先队列懂伐,就是优先级高的先出队。用在这道题就是距离小的优先出队,关于优先队列的这里就不过多阐述了
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,s,cnt; 4 int last[100005]; 5 int ans[100005]; 6 bool flag[100005]; 7 struct edge_{ 8 int e; 9 int w; 10 int next; 11 }edge[200006]; 12 struct node{ 13 int w; 14 int num; 15 bool operator<(const node &x) const//这里是重载运算符,因为优先队列默认是大的先出,所以我们改成小的先出 16 { 17 return x.w<w; 18 } 19 }; 20 inline void add(int u,int v,int w){//链式前向星 21 cnt++; 22 edge[cnt].e=v; 23 edge[cnt].w=w; 24 edge[cnt].next=last[u]; 25 last[u]=cnt; 26 } 27 inline int read(){ 28 int x=0,f=1; 29 char ch=getchar(); 30 while(ch>'9'||ch<'0') 31 { 32 if(ch=='-')f=-1; 33 ch=getchar(); 34 } 35 while(ch>='0'&&ch<='9') 36 { 37 x=(x<<1)+(x<<3)+(ch^48); 38 ch=getchar(); 39 } 40 return x*f; 41 } 42 priority_queue<node> q; 43 void djkstra() 44 { 45 ans[s]=0; 46 q.push((node){0,s}); 47 while(!q.empty()) 48 { 49 node head=q.top(); 50 q.pop(); 51 int x=head.num; 52 if(flag[x]) 53 continue; 54 flag[x]=1; 55 for(int i=last[x];i;i=edge[i].next) 56 { 57 int y=edge[i].e; 58 if(ans[y]>ans[x]+edge[i].w) 59 { 60 ans[y]=ans[x]+edge[i].w; 61 if(!flag[y]) 62 { 63 q.push((node){ans[y],y}); 64 } 65 } 66 } 67 } 68 } 69 int main() 70 { 71 n=read(),m=read(),s=read(); 72 for(int i=1;i<=n;i++) 73 { 74 ans[i]=0x7fffffff; 75 } 76 while(m--) 77 { 78 int u,v,d; 79 u=read(),v=read(),d=read(); 80 add(u,v,d); 81 } 82 djkstra(); 83 for(int i=1;i<=n;i++)printf("%d ",ans[i]); 84 }
Bell-man算法:判负环,效率低,判连通块
这个玩意儿的原理就是用边来松弛,按照输入的边的顺序松弛两端的点,所以要做n-1次操作才能保证松弛完毕(前提是没有负环,不然会一直松弛下去),所以我们就用这一特性判负环
1 #include<bits/stdc++.h> 2 using namespace std; 3 int f,n,m,w,cnt; 4 int last[100005]; 5 int dis[100005]; 6 struct edge_{ 7 int root; 8 int to; 9 int w; 10 int next; 11 }edge[200006]; 12 inline void add(int u,int v,int w){ 13 cnt++; 14 edge[cnt].root=u; 15 edge[cnt].to=v; 16 edge[cnt].w=w; 17 edge[cnt].next=last[u]; 18 last[u]=cnt; 19 } 20 bool bellman() 21 { 22 for(int i=1;i<=n;i++) 23 { 24 for(int j=1;j<=cnt;j++) 25 { 26 if(dis[edge[j].to]>dis[edge[j].root]+edge[j].w) 27 { 28 dis[edge[j].to]=dis[edge[j].root]+edge[j].w; 29 if(i==n)return true; 30 } 31 } 32 } 33 return false; 34 } 35 int main() 36 { 37 scanf("%d",&f); 38 while(f--) 39 { 40 cnt=0; 41 memset(dis,0x3f,sizeof(dis)); 42 dis[1]=0; 43 scanf("%d%d%d",&n,&m,&w); 44 for(int i=1;i<=m;i++) 45 { 46 int s,e,t; 47 scanf("%d%d%d",&s,&e,&t); 48 add(s,e,t); 49 add(e,s,t); 50 } 51 for(int i=1;i<=w;i++) 52 { 53 int s,e,t; 54 scanf("%d%d%d",&s,&e,&t); 55 add(s,e,-t); 56 } 57 if(bellman())printf("YES\n"); 58 else printf("NO\n"); 59 } 60 return 0; 61 }
Spfa算法:判负环,Bellman的进阶
这个避免了不必要的更新,类似于BFS,没次更新一个点,就把它加入队列,接着更新下去,减少了不必要的更新,但是关于SPFA,它死了
1 #include<bits/stdc++.h> 2 #define inf 0x3f3f3f3f 3 using namespace std; 4 int n,m,t; 5 int b[10005],c[10005]; 6 struct node{ 7 int y,time,next; 8 }edge[20010]; 9 int pre[10005],cnt=0; 10 int vis[10005],flag[10005],nums[10005];//nums记录入队次数 11 void add(int x,int y,int k) 12 { 13 edge[cnt].y=y, edge[cnt].time=k, edge[cnt].next=pre[x]; 14 pre[x]=cnt++; 15 } 16 queue<int>q; 17 bool SPFA(int s,int n) 18 { 19 memset(vis,inf,sizeof(vis)); 20 vis[s]=0;//初始化 21 flag[s]=1,nums[s]++;//标记,次数+1 22 q.push(s); 23 while(!q.empty()) 24 { 25 int x=q.front(); 26 q.pop();//出队 27 flag[x]=0;//标记不在队列 28 for(int i=pre[x]; ~i; i=edge[i].next)//遍历连通的点 29 { 30 int y=edge[i].y; 31 if(vis[y]>vis[x]+edge[i].time)//更新 32 { 33 vis[y]=vis[x]+edge[i].time; 34 if(!flag[y]) 35 { 36 q.push(y); 37 flag[y]=1;//标记 38 nums[y]++;//加入次数 39 if(nums[y]>n)//存在负圈 40 return false; 41 } 42 } 43 } 44 } 45 return true; 46 } 47 48 int main() 49 { 50 scanf("%d%d%d",&n,&m,&t) 51 memset(pre,-1,sizeof(pre)); 52 for(int i=0;i<n;i++) 53 { 54 int x,y,k; 55 cin>>x>>y>>k; 56 add(x,y,k); 57 add(y,x,k); 58 } 59 for(int i=0;i<m;i++) 60 cin>>b[i]; 61 for(int i=0;i<t;i++) 62 cin>>c[i]; 63 int minn=inf; 64 for(int i=0;i<m;i++) 65 { 66 SPFA(b[i],n); 67 for(int j=0;j<t;j++) 68 minn=min(minn,vis[c[j]]); 69 } 70 cout<<minn<<endl; 71 }
次短路
这个玩意儿嘛,顾名思义就是除了最短路后最短的路,也就是第二短路,用dijsktra就行了,出队两次。因为第一次代表到这个点的最短路,第二次就代表搜到第二次也就是第二短路了,只需要把打标记的地方改一下就行了。代码就在下面的k短路哪儿把k改成2就行了
而第二种方法就是用两个数组,记录最短路和次短路,然后更新的时候注意一下就行了(到n点的次短路。0代表最短路,1代表次短路)。
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,cnt; 4 int dis[1000005][2]; 5 int last[1000005]; 6 struct node{ 7 int to; 8 int w; 9 int pre; 10 }edge[1000005]; 11 struct point{ 12 int num; 13 int len; 14 bool operator<(const point &x )const{ 15 return len>x.len; 16 } 17 }; 18 queue<point> q; 19 void add(int u,int v,int w) 20 { 21 cnt++; 22 edge[cnt].to=v; 23 edge[cnt].w=w; 24 edge[cnt].pre=last[u]; 25 last[u]=cnt; 26 } 27 void d() 28 { 29 q.push(point{1,0}); 30 while(!q.empty()) 31 { 32 point head=q.front(); 33 q.pop(); 34 if(dis[head.num][1]<head.len)continue; 35 int d=head.len; 36 for(int i=last[head.num];i;i=edge[i].pre) 37 { 38 int d2=d+edge[i].w; 39 if(dis[edge[i].to][0]>d2)//更新最短路 40 { 41 swap(dis[edge[i].to][0],d2);//这么做后可以继续更新次短路 42 q.push(point{edge[i].to,dis[edge[i].to][0]}); 43 } 44 if(d2>dis[edge[i].to][0]&&d2<dis[edge[i].to][1])//更新次短路 45 { 46 dis[edge[i].to][1]=d2; 47 q.push(point{edge[i].to,dis[edge[i].to][1]}); 48 } 49 } 50 } 51 } 52 int main() 53 { 54 memset(dis,0x3f,sizeof(dis)); 55 dis[1][0]=0; 56 scanf("%d%d",&n,&m); 57 for(int i=1;i<=m;i++) 58 { 59 int x,y,w; 60 scanf("%d%d%d",&x,&y,&w); 61 add(x,y,w); 62 add(y,x,w); 63 } 64 d(); 65 cout<<dis[n][1]; 66 return 0; 67 }
K短路
这玩意儿就更变态了,其实还是之前的,首先暴力是肯定行的(暴力万岁)
1 #include<bits/stdc++.h> 2 using namespace std; 3 inline int read(){int a;scanf("%d",&a);return a;} 4 struct node 5 { 6 int v,x; 7 bool operator <(const node &a)const{return a.v<v;} 8 }; 9 int hea[1010],nxt[10010],to[10010],w[10010],f[1010],tot; 10 priority_queue<node> q; 11 int main() 12 { 13 int n=read(),m=read(),k=read(),x; 14 for(int i=1;i<=m;i++) 15 { 16 nxt[++tot]=hea[x=read()]; 17 to[tot]=read(); 18 w[tot]=read(); 19 hea[x]=tot; 20 } 21 q.push((node){0,n}); 22 while(!q.empty()) 23 { 24 node u=q.top(); 25 q.pop(); 26 if(u.x==1)printf("%d\n",u.v); 27 if(f[u.x]>=k)continue; 28 f[u.x]++; 29 if(f[1]>=k)break; 30 for(int i=hea[u.x];i;i=nxt[i]) 31 q.push((node){u.v+w[i],to[i]}); 32 } 33 for(int i=f[1]+1;i<=k;i++) 34 puts("-1"); 35 return 0; 36 }
然后就是很神奇的A*了
A*是一种启发式搜索,我们不会盲目的搜,而是有一个大概方向懂吧,就像你在一个小岛的边缘,你要往小岛中心走,不一定知道小岛中心在哪儿,但是肯定不会沿着边缘或者往海里走吧大概就是这个意思。而这里的估价函数就是这个点到终点的最短距离,入队的时候加上这玩意儿就行了,相比起暴力,A*避免了搜索其它节点的次数很多,有效降低缩小范围
1 #include<bits/stdc++.h> 2 using namespace std; 3 int dis[200005]; 4 int last1[200005],last2[200005]; 5 bool flag[200005]; 6 int n,m,cnt,ans,sum,k; 7 struct _edge{ 8 int to; 9 int w; 10 int pre; 11 }edge1[200005],edge2[200005]; 12 struct node1{ 13 int v; 14 int w; 15 bool operator <(const node1 &x)const{ 16 return w>x.w; 17 } 18 }; 19 20 struct node2{ 21 int v; 22 int w; 23 bool operator <(const node2 &x)const{ 24 return w+dis[v]>x.w+dis[x.v]; 25 } 26 }; 27 void add1(int u,int v,int w) 28 { 29 cnt++; 30 edge1[cnt].w=w; 31 edge1[cnt].to=v; 32 edge1[cnt].pre=last1[u]; 33 last1[u]=cnt; 34 } 35 void add2(int u,int v,int w) 36 { 37 edge2[cnt].w=w; 38 edge2[cnt].to=v; 39 edge2[cnt].pre=last2[u]; 40 last2[u]=cnt; 41 } 42 void d() 43 { 44 priority_queue<node1> q; 45 q.push((node1){1,0}); 46 while(!q.empty()) 47 { 48 node1 x=q.top(); 49 q.pop(); 50 if(flag[x.v])continue; 51 flag[x.v]=true; 52 for(int i=last2[x.v];i;i=edge2[i].pre) 53 { 54 if(dis[edge2[i].to]>dis[x.v]+edge2[i].w) 55 { 56 dis[edge2[i].to]=dis[x.v]+edge2[i].w; 57 q.push((node1){edge2[i].to,dis[edge2[i].to]}); 58 } 59 } 60 } 61 } 62 void Astar() 63 { 64 priority_queue<node2> q; 65 q.push((node2){n,0}); 66 while(!q.empty()) 67 { 68 node2 x=q.top(); 69 q.pop(); 70 if(x.v==1) 71 { 72 sum++; 73 printf("%d\n",x.w); 74 if(sum>=k)return ; 75 } 76 for(int i=last1[x.v];i;i=edge1[i].pre) 77 { 78 q.push((node2){edge1[i].to,x.w+edge1[i].w}); 79 } 80 } 81 } 82 int main() 83 { 84 memset(dis,0x3f,sizeof(dis)); 85 scanf("%d%d%d",&n,&m,&k); 86 dis[n]=0; 87 while(m--) 88 { 89 int x,y,z; 90 scanf("%d%d%d",&x,&y,&z); 91 add1(x,y,z); 92 add2(y,x,z);//反 93 } 94 d(); 95 Astar(); 96 for(int i=sum+1;i<=k;i++) 97 { 98 printf("-1\n"); 99 } 100 return 0; 101 }

