最近公共祖先LCA(我肯定是你的LCA)
P3379 【模板】最近公共祖先(LCA)
例子
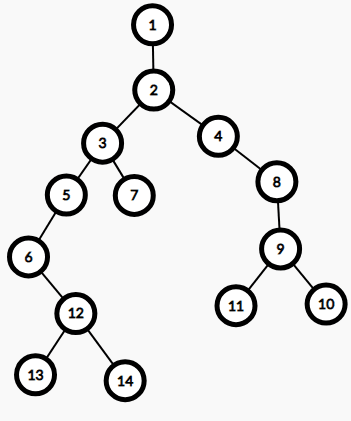
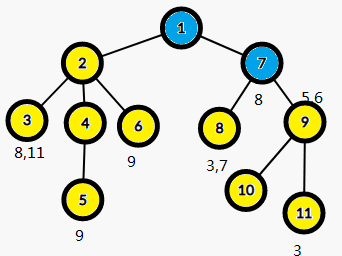
LCA(13,14)=12
LCA(13,7)=3
LCA(7,11)=2
LCA(11,2)=2
好了,了解以后我们就来康康怎么求吧
暴力LCA
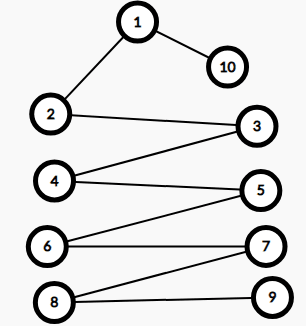
如果找LCA(6,8),我们就要先让它们的深度相等。此时(deep[1]=0)deep[6]=4,deep[8]=3,我们就先让节点6爬到节点5
然后就是愉快的一起爬
让它们一层一层地向上爬,知道爬到同一节点
但是都知道,一旦这棵树有点高,like this,就会TTT
因为这样爬着太慢了(青蛙爬树都知道跳着爬)
倍增LCA(在线操作)
所以我们升级了,会跳着爬了
但是怎么升呢,大家都知道,计算机和二进制都离不开关系
所以当然是按照2的次方来跳,不过我们不是从小往大(1,2,4,8,16,32,64...),而是从大到小(...64,,32,16,8,4,2,1)(因为从小到大加着会超过,到时候很麻烦)
所以我们跳的时候就还要计算一下你这么跳会到哪个节点去(不然你乱跳啊)
总所周知,1+1=2(这不是废话吗)
1 void dfs(int x,int fa) 2 { 3 deep[x]=deep[fa]+1; 4 f[x][0]=fa; 5 for(int i=1;(1<<i)<=deep[x];i++) 6 { 7 f[x][i]=f[f[x][i-1]][i-1]; 8 } 9 for(int i=0;i<mp[x].size();i++) 10 { 11 if(mp[x][i]==fa)continue; 12 dfs(mp[x][i],x); 13 } 14 }
我们用f[i][j]表示第i个节点向上跳2^j高度后的祖先节点,我们就不用像个憨批一样去搜了(不然你和暴力有什么区别),他就等于2^(j-1)*2也就是向上跳两次2^(j-1)
所以f[i][j]=f[f[i][]j-1][j-1]
所以我们循坏j从小到大,这样就可以用小的来递推大的了
然后搜索的时候顺便把深度也计算了
预处理完了,我们就要开始干正事了
1 int LCA(int x,int y) 2 { 3 if(deep[x]<deep[y])swap(x,y); 4 for(int i=log2(deep[x]);i>=0;i--) 5 if(deep[x]-(1<<i)>=deep[y]) 6 x=f[x][i]; 7 if(x==y)return x; 8 for(int i=log2(deep[x]);i>=0;i--) 9 { 10 if(f[x][i]!=f[y][i]) 11 { 12 x=f[x][i]; 13 y=f[y][i]; 14 } 15 } 16 return f[x][0]; 17 }
我们先让两个节点到达同一高度(为了方便计算,我们把高的放前面)
然后向上爬
先判断是否在同一点(因为存在两者的祖先是其中一个节点的可能,就是你和你爸的最近公共祖先是你爸)
然后一起向上跳跳跳(jump!!!)
为了避免两者计算出的公共祖先不是最近的(例如你爷爷也是你和你爸的公共祖先)
我们只跳到公共祖先的下一层,也就是第十排的判断
最后再输出它们的最近公共祖先就好了
1 #include<bits/stdc++.h> 2 #define N 500005 3 using namespace std; 4 int n,m,root; 5 int f[N][21]; 6 int deep[N]; 7 vector<int> mp[N]; 8 inline int read(){ 9 int x=0,f=1; 10 char ch=getchar(); 11 while(ch<'0'||ch>'9'){ 12 if(ch=='-') 13 f=-1; 14 ch=getchar(); 15 } 16 while(ch>='0'&&ch<='9'){ 17 x=(x<<1)+(x<<3)+(ch^48); 18 ch=getchar(); 19 } 20 return x*f; 21 } 22 void dfs(int x,int fa) 23 { 24 deep[x]=deep[fa]+1; 25 f[x][0]=fa; 26 for(int i=1;(1<<i)<=deep[x];i++) 27 { 28 f[x][i]=f[f[x][i-1]][i-1]; 29 } 30 for(int i=0;i<mp[x].size();i++) 31 { 32 if(mp[x][i]==fa)continue; 33 dfs(mp[x][i],x); 34 } 35 } 36 int LCA(int x,int y) 37 { 38 if(deep[x]<deep[y])swap(x,y); 39 for(int i=log2(deep[x]);i>=0;i--) 40 if(deep[x]-(1<<i)>=deep[y]) 41 x=f[x][i]; 42 if(x==y)return x; 43 for(int i=log2(deep[x]);i>=0;i--) 44 { 45 if(f[x][i]!=f[y][i]) 46 { 47 x=f[x][i]; 48 y=f[y][i]; 49 } 50 } 51 return f[x][0]; 52 } 53 int main() 54 { 55 deep[0]=-1; 56 n=read(),m=read(),root=read(); 57 for(int i=1;i<n;i++) 58 { 59 int a,b; 60 a=read(),b=read(); 61 mp[a].push_back(b); 62 mp[b].push_back(a); 63 } 64 dfs(root,0); 65 while(m--) 66 { 67 int a,b; 68 a=read(),b=read(); 69 printf("%d\n",LCA(a,b)); 70 } 71 return 0; 72 }
Tarjan求LCA(离线操作)
首先,我们来理解一下离线操作。就是输入完问题后一次性解决。而在线操作就是每输入一个问题就可以立即得出答案。其实你硬要把离线做成在线也行(但是每次都要初始化,很麻烦。离线之所以是离线,说明做的方法有共通之处,有些一次就可以解决)
首先我们需要的数组如下
flag []表示是否已经回溯(被搜索过)
fa[]寻找父亲节点
ans[]记录每个问题的答案
e[]链式前向星存边
q[]记录问题的vector
注意,这里的问题要存两个,具体原因我后面会讲到
我们用的是DFS(深度优先搜索),因为公共祖先是父亲节点嘛,这样的话保证一个点之前的都是自己的祖先(能懂吧,毕竟只是一棵树)
看看问题
3 8 3 11 6 9 5 9 7 8
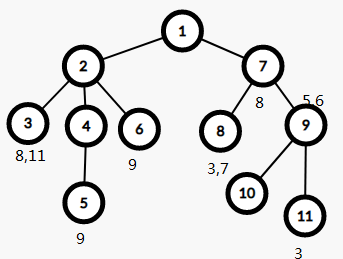
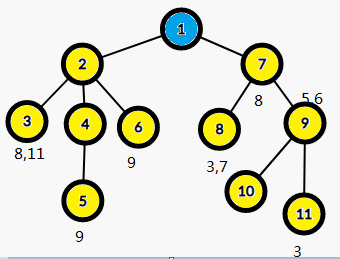
因为8,11都未被搜索,所以不做操作,但是回溯的时候要更新fa[]。因为初始值都是自己,回溯才连接父亲节点
此时可以用并查集,方便路径压缩 当然你要暴力也没意见
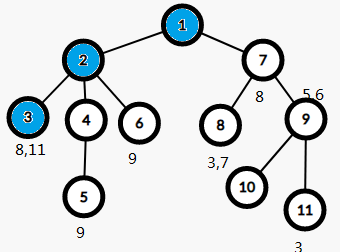
同理
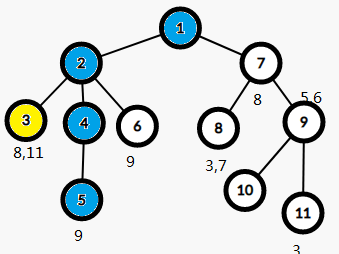
不做操作
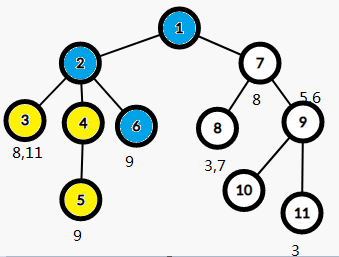
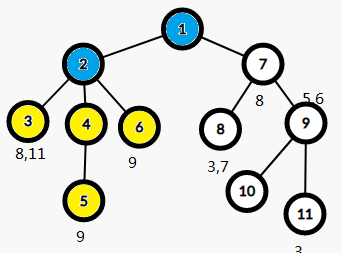
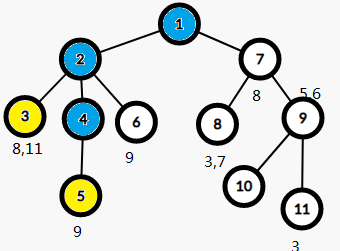
关键的来了,众所周知,最近公共祖先就是两个点的祖先节点所构成的链的最先相交的地方,此时蓝色的都是8的父亲,所以我们只需要搜索另外一个点的父亲,而这个操作就可以考虑并查集,当然不用也行。(其实都差不多)一层一层向上搜索,直到一个fa[]等于自己的节点。
可以看出,fa[]等于自己的点要不就是正在搜索没有回溯(也就是当前节点的祖先),要不就是没有被搜索。
怎么保证第一个搜索的一定是蓝色的呢。我们可以假设第一个fa[]等于自己的是没有被搜索的,但是如果没有被搜索的话这个点也不会被搜索,说明这个点的fa[]也等于自己,这是矛盾的,所以不成立。
所以LCA(3,8)=1
但是这里并不能计算 7,8.因为此时7并没有被打上标记(黄色)
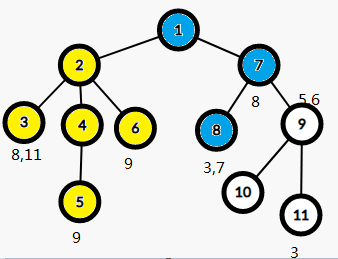
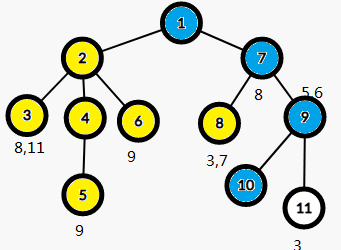
LCA(3,11)=1
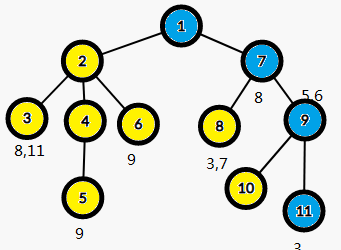
LCA(5,9)=1
LCA(6,9)=1
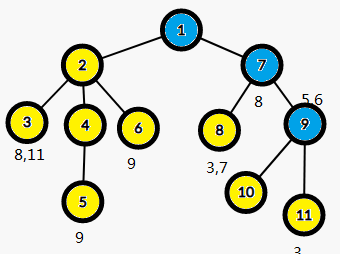
LCA(7,8)=7'
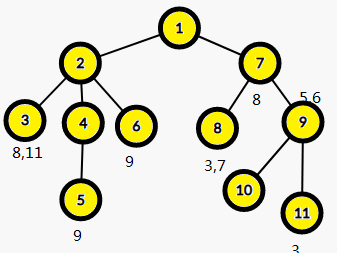
好了,这样就做完了时间复杂度差不多是O(n+q)
康康代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=500010; 4 const int M=500010; 5 int n,m,s,cnt; 6 int last[N];//前向星 7 int fa[N];//记录父亲 8 int ans[M];//记录答案 9 bool flag[N];//判断是否被搜索 10 struct node{//记录边的 11 int to,pre; 12 }e[2*M]; 13 struct question{//还要记录编号,方便保存并且输出答案 14 int to,num; 15 }; 16 vector<question>q[N];//记录问题 17 void add(int x,int y) 18 { 19 cnt++; 20 e[cnt].to=y; 21 e[cnt].pre=last[x]; 22 last[x]=cnt; 23 } 24 int get(int x)//找父亲节点 25 { 26 return fa[x]==x?x:(fa[x]=get(fa[x])); 27 } 28 void dfs(int u,int root)//最核心部分 29 { 30 for(int i=last[u];i;i=e[i].pre) 31 { 32 if(e[i].to==root)continue; 33 dfs(e[i].to,u); 34 fa[e[i].to]=u; 35 } 36 for(int i=0;i<q[u].size();i++) 37 if(flag[q[u][i].to]) 38 ans[q[u][i].num]=get(q[u][i].to); 39 flag[u]=1; 40 } 41 int main() 42 { 43 scanf("%d%d%d",&n,&m,&s); 44 for(int i=1;i<=n;i++)fa[i]=i; 45 for(int i=1;i<n;i++) 46 { 47 int u,v; 48 scanf("%d%d",&u,&v); 49 add(u,v); 50 add(v,u); 51 } 52 for(int i=1;i<=m;i++) 53 { 54 int x,y; 55 scanf("%d%d",&x,&y); 56 q[x].push_back((question){y,i});//一定要存两次,因为你不知道那个先被搜索到 57 q[y].push_back((question){x,i}); 58 } 59 dfs(s,0); 60 for(int i=1;i<=m;i++) 61 { 62 printf("%d\n", ans[i]);//避免TTT 63 } 64 return 0; 65 }
好了,就是这样了。喜欢的话点赞支持一下哦