最大子段(阵)和
P1115 最大子段和
这是一道DP经典题(感觉什么都经典)也是很常见的一个题型,具体思路就是用sum记录一个前缀和,从a[1]遍历到a[n]每次,加上去,但是一旦sum成了负数,就没必要前缀和了,重新赋值0(因为前面就是累赘了)然后,就做出来了........
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,x,maxx,sum; 4 int main() 5 { 6 scanf("%d%d",&n,&sum); 7 maxx=sum; 8 //先记录第一个值,因为所有都是负数时,maxx就会是0,所以要不预先处理,要不赋值负无穷 9 while(--n) 10 { 11 scanf("%d",&x); 12 sum=max(sum,0);//看负数就不要了 13 sum+=x;//加上去 14 maxx=max(maxx,sum);//曲最大子段和 15 } 16 printf("%d",maxx); 17 }
HDU To The Max
学完了最大子段和后,该学最大子阵和了(欸嘿嘿)。对于求二维的这玩意儿,我们压成一位就可以了。肯定会有人问,怎么压成一维?

康康这个样例,我们枚举要选取的矩阵的宽度
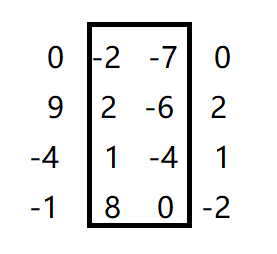
(不要问我为什么是竖着的,因为方便一些)
然后我们就把这两竖行压成一竖行
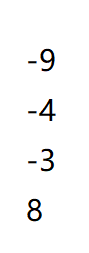
我知道竖着难受,但是....我懒得改了
然后我们用正规的最大子段和求就行了啦
至于这个压行的操作,我们记录一个前缀和,枚举区间左右边界即可
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,ans; 4 int mp[105][105]; 5 int qzh[105][105]; 6 int main() 7 { 8 while(cin>>n) 9 { 10 ans=-1e9;//一定要负无穷,避免后边负数,ans为0 11 for(int i=1;i<=n;i++) 12 for(int j=1;j<=n;j++) 13 scanf("%d",&mp[i][j]);//输入 14 for(int i=1;i<=n;i++) 15 for(int j=1;j<=n;j++) 16 qzh[i][j]=qzh[i][j-1]+mp[i][j];//前缀和(变量名生动形象) 17 for(int i=1;i<=n;i++)//枚举区间右下标 18 { 19 for(int j=0;j<i;j++)//枚举区间 左下标 20 { 21 int sum,maxx;//剩下就是最大子段和啦 22 sum=maxx=qzh[1][i]-qzh[1][j]; 23 for(int l=2;l<=n;l++) 24 { 25 int x=qzh[l][i]-qzh[l][j]; 26 sum=max(sum,0); 27 sum+=x; 28 maxx=max(maxx,sum); 29 } 30 ans=max(ans,maxx); 31 } 32 } 33 cout<<ans<<endl; 34 } 35 }

