【中国剩余定理（孙子定理）】

中国剩余定理，又称孙子定理（什么名字啊）是中国古代求解一次同余式组（见同余）的方法。是数论中一个重要定理。首先来一个小！例！题！吧！

注释：三数为a b c，余数分别为 m1 m2 m3，%为求  今年 余计算，&&是“且”运算。

1、分别找出能被两个数整除，而满足被第三个整除余一的最小的数。

k1%b==k1%c==0 && k1%a==1;

k2%a==k2%c==0 && k2%b==1;

k3%a==k3%b==0 && k3%c==1;

2、将三个未知数乘对应数字的余数再加起来，减去这三个数的最小公倍数的整数倍即得结果。

Answer = k1×m1 + k2×m2 + k3×m3 - P×(a×b×c);

P为满足Answer > 0的最大整数；

或者 Answer = (k1×m1 + k2×m2 + k3×m3)%(a×b×c) ;

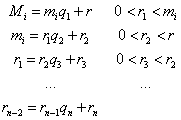
我们来小小的证明一波

　

　设M=m1*m2*......*mn

　　Mi=M/mi

　　设Mi的逆元为Mi^(-1)(mod mi)

　　有Mi*Mi^(-1)≡1(mod mi)

　　ai*Mi*Mi^(-1)≡ai(mod mi)

　　对于所有的j不等于i

　　ai*Mi*Mi^(-1)≡0(mod mj)

　　所以答案就是所有ai*Mi*Mi^(-1)（mod p）的值

P3868 [TJOI2009]猜数字

#include<bits/stdc++.h>
using namespace std;
long long x,y;
long long a[15],b[15];
long long n;
void exgcd(long long A,long long B)
{
    if(B==0)
    {
        x=1;
        y=0;
        return;
    }
    exgcd(B,A%B);
    long long z=x;
    x=y;
    y=z-(A/B)*y;
}
long long fast(long long a1,long long b1,long long mod)
{
    long long ans=0;
    a1%=mod;
    b1%=mod;
    while(b1)
    {
        if(b1&1)
        {
            ans=(ans+a1)%mod;
        }
        b1>>=1;
        a1=(a1+a1)%mod;
    }
    return ans;
}
long long china()
{
    long long ans=0;
    long long M=1;
    for(long long i=1;i<=n;i++)
        M*=b[i];
    for(long long i=1;i<=n;i++)
    {
        long long m=M/b[i];
        exgcd(m,b[i]);
        while(x<0)
            x+=b[i]; 
        x%=b[i];
        ans=(ans+fast(x,fast(m,(a[i]+M)%M,M),M)+M)%M;
    }
    return ans;
}
int main()
{
    cin>>n;
    for(long long i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
    }
    for(long long i=1;i<=n;i++)
    {
        scanf("%lld",&b[i]);
    }
    cout<<china();
    return 0;
}