【字典树(我的字典我做主)】
一、Tried的概念
又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
来了解一下存储方式: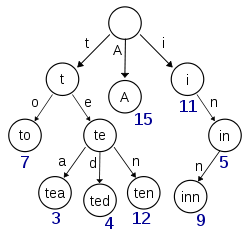
此时我们也了解了一些字典树的特点
1、根节点不包含字符。
2、除根节点外每一个节点都只包含一个字符。
3、从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串; 每个节点的所有子节点包含的字符都不相同。
二、Trie的操作
常见的操作有插入、查找、删除。(由于博客主还没有学删除操作,所以.....)
在这棵树中,我们会用一个数组来存每一个节点的编号,根节点编号一般为0。
然后,ch[i][j]表示i的编号为j的子节点,所以当ch[i][j]=0时节点不存在。
最后还有个val数组,是专门用来存附加条件的。
必要元素
我们需要val数组来记录比较重要的数值(例如某个单词在x页,在单词结尾记录x,或一个词有,记录为1)
ch数组来建树,一个点连向几个点,方便后面查找操作。
sz记录编号
int ch[N][26]; int val[N]; int sz;
初始化
注意,ch数组没必要全部初始化,会浪费很多时间,当必要的时候再初始化。
void clean() { sz=1; memset(ch[0],0,sizeof ch[0]); memset(val,0,sizeof(val)); }
插入
插入就是从字符串的第一位开始遍历一直到最后,已经有的节点就利用一下(利用前缀节省时间)然后没有的时候就新开一个
(这里的get就是s[i]-'a',当然,不一定非要是a,按照题目变化)
void insert(char s[],int,sum) { int u=0;//根节点是0 for(int i=0;i<strlen(s);i++)//遍历 { int v=get(s[i]);//下一个点 if(!ch[u][v])//没有开,就开一下,初始化 { memset(ch[sz],0,sizeof(ch[sz])); ch[u][v]=sz; sz++; } u=ch[u][v];//继续搜 } val[u]=sum;//在末尾标记 }
查找
和插入差不多,但是当没有下一个点的时候直接返回没有找到。最后到结尾判断一下是否是字符串(万一是字串也会一路找下来)
int find(char s[]) { int u=0; for(int i=0;i<strlen(s);i++) { int v=get(s[i]); if(!ch[u][v])return 0; u=ch[u][v]; } if(!val[u])return 0; return 1; }
luogu P2580 于是他错误的点名开始了掌握了以上操作的可以看看,因为删除操作一般不是很常用
删除
当一道题需要用到删除的时候,一般都会想到直接删除末尾的标记,但是这样做的话有一个弊端
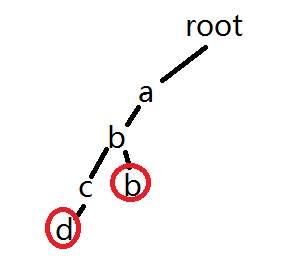
假设我们删除abcd
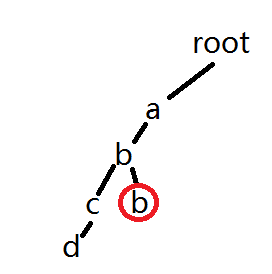
但是当我们下一次查找的时候,还是会按照abcd的顺序查找,当数据极端,就会造成时间浪费。所以我们要新开一个数组,cnt[u]表示节点u被经过的次数
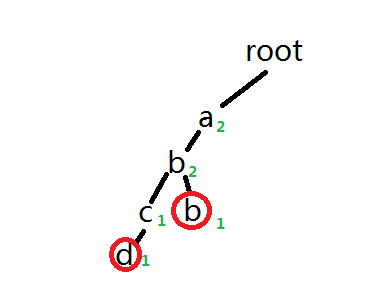
当我们删除的时候,把沿途的cnt[u]减一,当有一个节点的经过数为0的时候,说明这个节点没有搜索的必要,就会节省很多时间
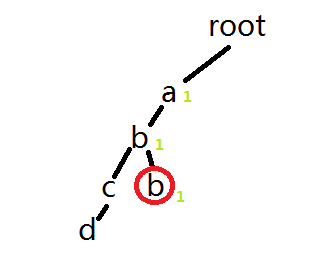
当我们想要搜索abcd是,搜索到b就会返回,而不会傻傻的搜到底部(当然这个只针对一定可以删除到的操作)
void delet(char s[]) { int u=0; for(int i=0;i<strlen(s);i++) { int v=get(s[i]); u=ch[u][v]; cnt[u]--; } val[u]=0; }
因为多了个cnt数组,所以插入的途中也要cnt[u]++
HDU5526这道题就是,因为防止搜索到与a[i],a[j]相同的数组,所以我们每次要从字典树里删除掉它,然后再加回去
#include<bits/stdc++.h> using namespace std; const int N=100010; bitset<32>s; int n,m,ans; int a[N]; struct Trie{ int ch[N][2]; int cnt[N]; int val[N]; int sz; void clean(){ memset(ch[0],0,sizeof ch[0]); memset(val,0,sizeof(val)); memset(cnt,0,sizeof cnt); sz=1; } int get(char a){return a;} void insert(int sum) { int u=0; for(int i=31;i>=0;i--) { int v=get(s[i]); if(!ch[u][v]) { memset(ch[sz],0,sizeof ch[sz]); ch[u][v]=sz; sz++; } u=ch[u][v]; cnt[u]++; } val[u]=sum; } void delet() { int u=0; for(int i=31;i>=0;i--) { int v=get(s[i]); u=ch[u][v]; cnt[u]--; } } int find() { int u=0; for(int i=31;i>=0;i--) { int v=get(s[i]); if(!cnt[ch[u][(v+1)%2]])u=ch[u][v]; else u=ch[u][(v+1)%2]; } return val[u]; } }T; int main() { int t; scanf("%d",&t); while(t--) { T.clean(); ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); s=a[i]; T.insert(i); } for(int i=1;i<=n;i++) { s=a[i]; T.delet(); for(int j=i+1;j<=n;j++) { s=a[j]; T.delet(); s=a[i]+a[j]; ans=max(ans,(a[i]+a[j])^a[T.find()]); s=a[j]; T.insert(j); } s=a[i]; T.insert(i); } printf("%d\n",ans); } return 0; }

