【常用算法总结——分治】
分治
分治,字面上的解释是"分而治之",就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在计算机科学中,分治法就是运用分治思想的一种很重要的算法。分治法是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)等等。
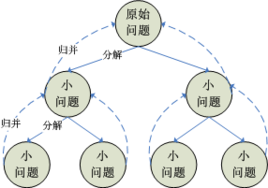
本质
在求解一个输入规模为n,而n的取值又很大的问题时,直接求解往往非常困难。这时,可以先分析问题本身所具有的某些特性,然后从这些特性出发,选择某些适当的设计策略来求解。这种方法,就是所谓的分治法。
适用条件
采用分治法解决的问题一般具有的特征如下:
1. 问题的规模缩小到一定的规模就可以较容易地解决。
2. 问题可以分解为若干个规模较小的模式相同的子问题,即该问题具有最优子结构性质。
3. 合并问题分解出的子问题的解可以得到问题的解。
4. 问题所分解出的各个子问题之间是独立的,即子问题之间不存在公共的子问题。
设计步骤
1. 划分步:把输入的问题划分为k个子问题,并尽量使这k个子问题的规模大致相同。
2. 治理步:当问题的规模大于某个预定的阈值n0时,治理步由k个递归调用组成。
3. 组合步:组合步把各个子问题的解组合起来,它对分治算法的实际性能至关重要,算法的有效性很大地依赖于组合步的实现。
分治法的关键是算法的组合步。究竟应该怎样合并,目前没有统一的模式,因此需要对具体问题进行具体分析,以得出比较好的合并算法。
例题请见黑白棋子的移动
二分查找
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。

算法要求
- 必须采用顺序存储结构。
2.必须按关键字大小有序排列。
算法复杂度
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
时间复杂度无非就是while循环的次数!
总共有n个元素,
渐渐跟下去就是n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O(h)=O(log2n)
折半查找法也称为二分查找法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是,将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法终止。如 果x<a[n/2],则我们只要在数组a的左半部继续搜索x(这里假设数组元素呈升序排列)。如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。
例题请见查找
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑以上摘自百度百科

