POJ 1980【Unit Fraction Partition】

 

 

 

描述

　　给出数字P,Q,A,N，代表将分数P/Q分解成至多N个分数之和，这些分数的分子全为1,且分母的乘积不超过A。例如当输入数据为2 3 120 3时，我们可以得到以下几种分法:

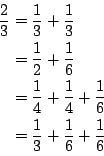
输入输出格式

输入

　　本题含有多组测试数据，每组给出四个数P，Q，A，N，其中 p,q <= 800, A <= 12000,N <= 7.当输入的四个数均为0时，代表测试结束.

输出

　　针对每组数据，输出共有多少种不同的分法。

 

输入输出样例

 

输入样例1

 

2 3 120 3
2 3 300 3
2 3 299 3
2 3 12 3
2 3 12000 7
54 795 12000 7
2 3 300 1
2 1 200 5
2 4 54 2
0 0 0 0

 

输出样例1

4
7
6
2
42
1
0
9
3

解题思路

　　这道题花了我两个小时。刚开始我用了最大公约数来求最小公倍数什么的，代码很麻烦，要同时约分什么的，但是其实只要几个简单易懂剪枝（只要你有足够的数学基本功）就行了，最后输出。

题解

 

#include<bits/stdc++.h>
using namespace std;
int ans,p,q,a,n;
void dfs(int dep,int pre,int fz,int fm,int sum)//深度，上一个的下标，当前分子，当前分母，当前乘积 
{
    if(sum>a)return;//乘积超过就返回 
    if(fz*q==fm*p)//直接最暴力的分母乘分母通分 
    {
        ans++;//方案数加加 
        return;
    }
    if(fz*q>fm*p||dep==n+1)return;//这个也靠自己理解，是指当前分数比目标分数大，还有分数数量超过了n 
    for(int i=pre;i<=a/sum;i++)//循环 
    {
        dfs(dep+1,i,fz*i+fm,fm*i,sum*i);//愉快的搜索 
    }
}
int main()
{
    while(cin>>p>>q>>a>>n)//注意格式 
    {
        if(q==0)return 0;//反正分母不为零 
        ans=0;//注意清空 
        dfs(1,1,0,1,1);//搜索 
        cout<<ans<<endl;//输出 
    }
    return 0;
}

 然而大家看一看这个程序的运行时间

Time:364

然后我在下次考试中优化了一下

 

#include<bits/stdc++.h>
using namespace std;
int p,q,a,n,qwe,ans;
void dfs(int fz,int fm,int dep,int pre,int sum)
{
    if(dep==qwe+1)
    {
        if(fz==0)
        {
            ans++;
        }
        return;
    }
    for(int i=pre;i<=a/sum;i++)
    {
        if(fz*i<fm)continue;
        if(i>fm*(qwe+1-dep)/fz)break;//优化
        dfs(fz*i-fm,fm*i,dep+1,i,sum*i);
    }
}
int main()
{
    while(cin>>p>>q>>a>>n&&q)
    {
        ans=0;
        for(qwe=1;qwe<=n;qwe++)
            dfs(p,q,1,1,1);
        cout<<ans<<endl;
    }
}

 

Time：56

 

　　再来看看另一种方法

解题思路

　　传入的参数与之前有所不同，这次的分子和分母是目标分数减去以枚举的分数剩下的分数值，再把分母枚举的范围剪枝一波，时间就大大减少了。

　　再看到13行：

　　　　　　我们先看枚举的起点，这里拿个两个参数作比较，pre是上一个分母的值，fm/fz是我们把这一个分数假装是最后一个，能取到的最大值，就是防止最后减出的值为负数，两者取大值。

　　　　　　再看枚举的重点，这里依旧有两个参数作比较，前者是防止乘积超出，后者是一种极端情况，把剩余分数值平均分给剩下所有的分数，即保证剩下的分数之和大于等于当前剩余分数值。

题解

 

#include<bits/stdc++.h>
using namespace std;
int p,q,a,n,ans;
void dfs(int fz,int fm,int sum,int dep,int pre) //剩余分子分母，乘积，深度，上一个分母 
{
    if(sum>a)return;//乘积超过 
    if(fz==0)//分子为零 
    {
        ans++;//方案数加加 
        return;
    }
    if(dep==n+1)return;//分数数量超过 
    for(int i=max(pre,fm/fz);i<=min(a/sum,(n+1-dep)*fm/fz);i++)//请见解题思路 
    {
        dfs(fz*i-fm,fm*i,sum*i,dep+1,i);//搜索 
    }
}
int main()
{
    while(cin>>p>>q>>a>>n)//以下都不需要注释了 
    {
        if(q==0)return 0;
        ans=0;
        dfs(p,q,1,1,1); 
        cout<<ans<<endl;
    }
}

 

我们再看看这一次代码的运行时间

 

Time：36

说实话，都没想到这么快（笑哭）。