YCOJ【切巧克力】

描述

超市里卖的巧克力都是高为H，宽为W的长方形，如下图所示。图中的高为3，宽为5。

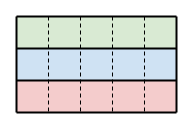
现在要把一整块巧克力切成三块，切的要求是：每次切的时候必须从所切的巧克力(长方形)的某条边的某个位置开始切，且必须一刀切断。切后分开的两块必须都是长方形(或正方形)。只能沿着每个11的方块的边线切，不能从中间切。现在要让切成的三块巧克力尽量平均，即让切出的最大一块所含11方块的数量减去最小一块的方块的数量的差值尽量小。

输入输出格式

输入

1行：2个整数H和W，表示一整块巧克力的高度和宽度

输出

第1行：1个整数，表示最大块与最小块的差值

输入输出样例

输入样例1

3 5

输出样例1

0

输入样例2

5 5

输出样例2

4

提示

样例说明1：横着切开，可以使最大块与最小块的差值为0

 

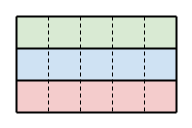
样例说明2：

 

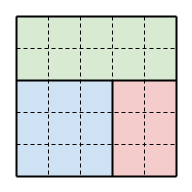
数据规模：

2<=H，W <=100000

 

　　

 

解题思路

　　这道题只需要把几种（某种意义上最优的答案）分别算出来，再比较输出即可。

题解

 

#include<bits/stdc++.h>
using namespace std;
long long qkl1(long long a,long long b)
{
    long long x,y,z;
    x=(a/3)*b;
    y=(a-a/3)*(b/2);
    z=a*b-x-y;
    return max(abs(x-y),max(abs(y-z),abs(x-z)));
}
long long qkl2(long long a,long long b)
{
    long long x,y,z;
    x=(a/3+1)*b;
    y=(a-a/3-1)*(b/2);
    z=a*b-x-y;
    return max(abs(x-y),max(abs(y-z),abs(x-z)));
}
long long qkl3(long long b,long long a)
{
    long long x,y,z;
    x=(a/3)*b;
    y=(a-a/3)*(b/2);
    z=a*b-x-y;
    return max(abs(x-y),max(abs(y-z),abs(x-z)));
}
long long qkl4(long long b,long long a)
{
    long long x,y,z;
    x=(a/3+1)*b;
    y=(a-a/3-1)*(b/2);
    z=a*b-x-y;
    return max(abs(x-y),max(abs(y-z),abs(x-z)));
}
int main()//总的就是四个函数计算后比较，可以自己试着理解一下 
{
    long long a,b;
    cin>>a>>b;
    if(a%3==0||b%3==0)cout<<0;//如果能平均分当然最好 
    else cout<<min(qkl1(a,b),min(qkl2(a,b),min(qkl3(a,b),min( qkl4(a,b),min(a,b) ) ) ) );//输出最优解 
    return 0;
}