matlab生成sin信号以及fft设置

f=4000; %信号频率为4KHz
fs=48000; %采样率为48KHz
t=(0:1/fs:1000/fs); %定义信号的时间范围
x=cos(2*pi*f*t); %生成信号

 

 

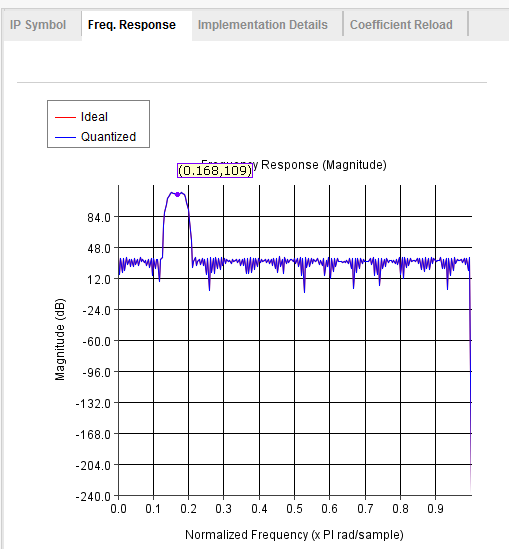
fir滤波器中的频响是0~pi，因此如果采样率是48KHz，如上图所示通带中心在0.168附近，那通带的信号频率应该是(48/2)*0.168 = 4KHz左右。

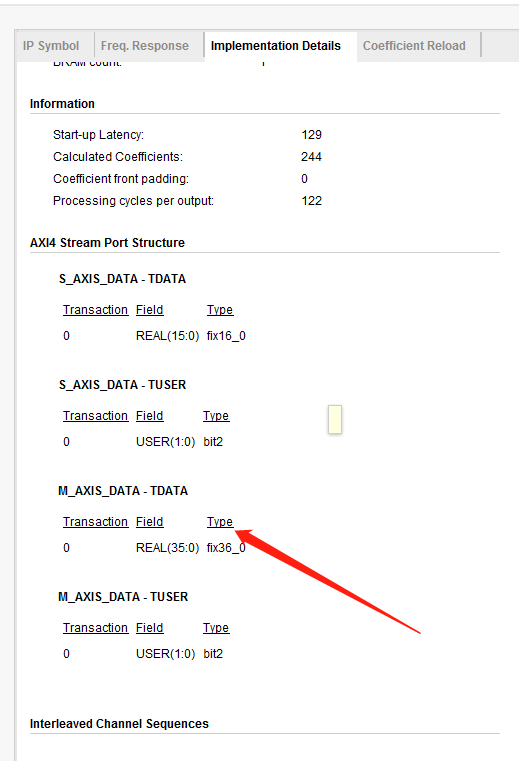
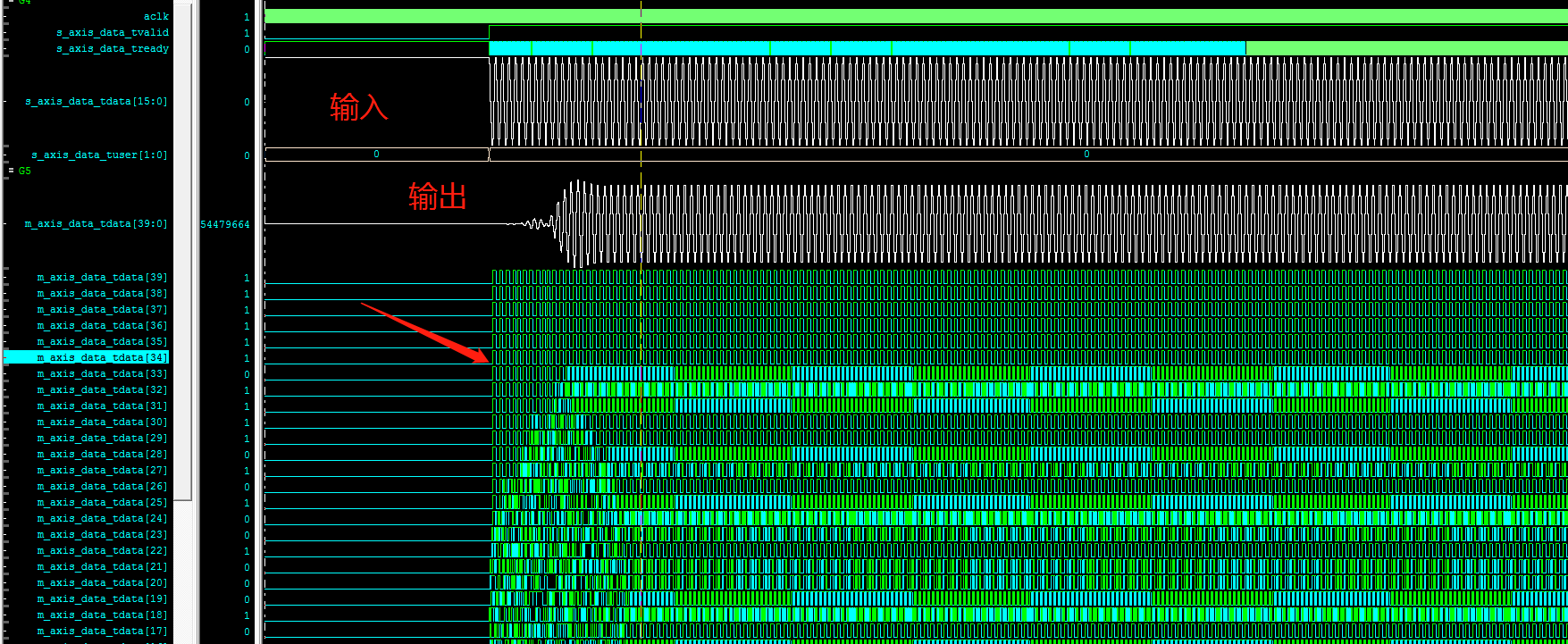
fir IP的输出实际的位宽和有效位宽可能不一致，如下图所示的IP输出位宽为40bit，实际有效位宽为36bit。有效带宽内包含两bit符号位，因此实际截位为bit34~bit19（截取16bit）。

本例中可以输入一个4KHz的正弦波，由于在通带内因此不会衰减，看输出的最高有效位在哪，实际测试最高有效位也是bit33，符号位为bit34.

 

 

FFT使用：

　　fft的IP使用和fix16_15还是fix16_0没有关系，不影响计算的结果，重点在于量化的精度，如果精度差太大就和matlab的结果差太大导致数值上对不上。

影响fft精度的因素：

　　1. phase factor 旋转因子的位宽

　　2. 输入数据的位宽（数据有效位宽为16bit时，fft的输入放到只24bit，相当于输入数据乘以256，也可以改善精度）

　　3. 输入数据的范围过小也影响精度，应该同比例放大至位宽范围内最大值。

　　

　　4. 动态配置IP时，需要仔细查看文档pg109，Page55 讲的注意事项及方法。

　　5. 对于Non-realtime以及realtime的不同模式，IP输出的接口信号是不一样的，动态配置也和这个模式有关系。

　　6. 没啥特殊情况，建议使用realtime模式

　　7. 某些情况下，fft和ifft的输出结果实部可能很接近，不必纠结于此，看matlab对应的结果即可，另外此时虚部相差很大。

　　8. 输入是16bit的情况下，如果输入值很小（比方最大两三百这种），那么输出的值和matlab的偏差会很大，极有可能连符号位都对不上，其实是因为精度导致的，

　　此时把fft的输入设置成24bit，将16bit数据映射到高16bit，低8bit可以理解为作为fft运算中间值的精度扩展位，运算的结果再取高32位，可以极大的改善精度，基本能和matlab对应上。