机器学习-回归和聚类

流程图

 

 

回归和聚类

1 回归和聚类

2 线性回归
3 欠拟合与过拟合
4 岭回归

5 分类算法：逻辑回归

6 模型保存与加载

7 无监督学习 K-means算法

"""
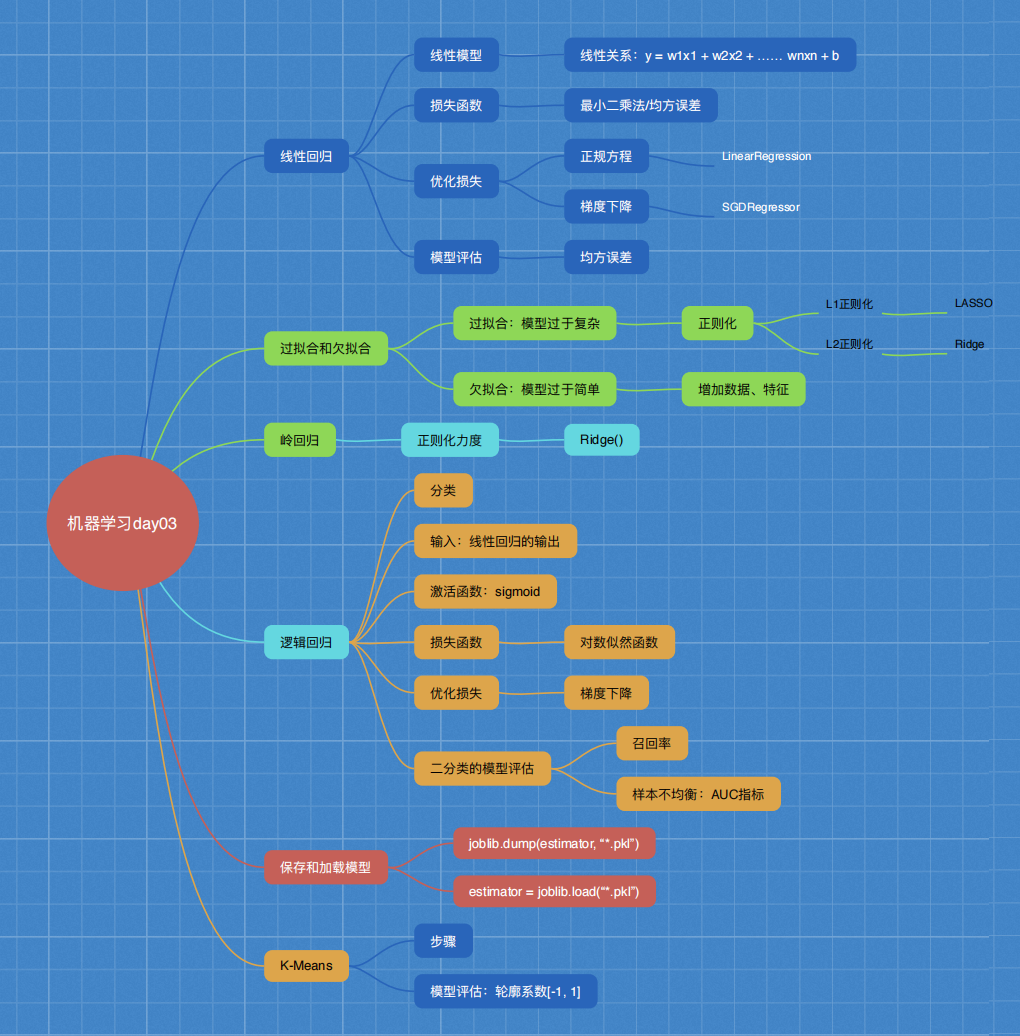
回归和聚类

线性回归
欠拟合与过拟合
岭回归

分类算法：逻辑回归

模型保存与加载

无监督学习 K-means算法


4.1 线性回归
    回归问题：
        目标值 - 连续型的数据
    4.1.1 线性回归的原理
        2 什么是线性回归
            函数关系 特征值和目标值
            线型模型
                线性关系
            y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
              = wTx + b
            数据挖掘基础
            y = kx + b
            y = w1x1 + w2x2 + b
            y = 0.7x1 + 0.3x2
            期末成绩：0.7×考试成绩+0.3×平时成绩
            [[90, 85],
            []]
            [[0.3],
            [0.7]]
            [8, 2] * [2, 1] = [8, 1]
            广义线性模型
                非线性关系？
                线性模型
                    自变量一次
                     y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
                    参数一次
                     y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b
                线性关系&线性模型
                线性关系一定是线性模型
                线性模型不一定是线性关系
         4.1.2 线性回归的损失和优化原理（理解记忆）
            目标：求模型参数
                模型参数能够使得预测准确
            真实关系：真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
            随意假定：预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
            损失函数/cost/成本函数/目标函数：
                最小二乘法
            优化损失
                优化方法？
                正规方程
                    天才 - 直接求解W
                    拓展：
                    1)
                        y = ax^2 + bx + c
                        y' = 2ax + b = 0
                        x = - b / 2a
                    2)
                        a * b = 1
                            b = 1 / a = a ^ -1
                        A * B = E
                        [[1, 0, 0],
                        [0, 1, 0],
                        [0, 0, 1]]
                        B = A ^ -1

                梯度下降
                    勤奋努力的普通人
                        试错、改进
            4.1.4 波士顿房价预测
                流程：
                    1）获取数据集
                    2）划分数据集
                    3）特征工程：
                        无量纲化 - 标准化
                    4）预估器流程
                        fit() --> 模型
                        coef_ intercept_
                    5）模型评估
            回归的性能评估：
                均方误差
            4 正规方程和梯度下降对比
4.2 欠拟合与过拟合
    训练集上表现得好，测试集上不好 - 过拟合
    4.2.1 什么是过拟合与欠拟合
        欠拟合
            学习到数据的特征过少
            解决：
                增加数据的特征数量
        过拟合
            原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点
            解决：
                正则化
                    L1
                    损失函数 + λ惩罚项
                    LASSO
                    L2 更常用
                    损失函数 + λ惩罚项
                    Ridge - 岭回归
4.3 线性回归的改进-岭回归
    4.3.1 带有L2正则化的线性回归-岭回归
        alpha 正则化力度=惩罚项系数
4.4 分类算法-逻辑回归与二分类
    4.4.1 逻辑回归的应用场景
        广告点击率 是否会被点击
        是否为垃圾邮件
        是否患病
        是否为金融诈骗
        是否为虚假账号
        正例 / 反例
    4.4.2 逻辑回归的原理
        线型回归的输出 就是 逻辑回归 的 输入
        激活函数
            sigmoid函数 [0, 1]
            1/(1 + e^(-x))
        假设函数/线性模型
            1/(1 + e^(-(w1x1 + w2x2 + w3x3 + …… + wnxn + b)))
        损失函数
            (y_predict - y_true)平方和/总数
            逻辑回归的真实值/预测值 是否属于某个类别
            对数似然损失
            log 2 x
        优化损失
            梯度下降
    4.4.4 案例：癌症分类预测-良／恶性乳腺癌肿瘤预测
        恶性 - 正例
        流程分析：
            1）获取数据
                读取的时候加上names
            2）数据处理
                处理缺失值
            3）数据集划分
            4）特征工程：
                无量纲化处理-标准化
            5）逻辑回归预估器
            6）模型评估
    真的患癌症的，能够被检查出来的概率 - 召回率
    4.4.5 分类的评估方法
        1 精确率与召回率
            1 混淆矩阵
                TP = True Possitive
                FN = False Negative
            2 精确率(Precision)与召回率(Recall)
                精确率
                召回率 查得全不全
                工厂 质量检测 次品 召回率
            3 F1-score 模型的稳健型
       总共有100个人，如果99个样本癌症，1个样本非癌症 - 样本不均衡
       不管怎样我全都预测正例(默认癌症为正例) - 不负责任的模型
           准确率：99%
           召回率：99/99 = 100%
           精确率：99%
           F1-score: 2*99%/ 199% = 99.497%
           AUC:0.5
                TPR = 100%
                FPR = 1 / 1 = 100%
       2 ROC曲线与AUC指标
            1 知道TPR与FPR
                TPR = TP / (TP + FN) - 召回率
                    所有真实类别为1的样本中，预测类别为1的比例
                FPR = FP / (FP + TN)
                    所有真实类别为0的样本中，预测类别为1的比例
4.5 模型保存和加载
4.6 无监督学习-K-means算法
    4.6.1 什么是无监督学习
        没有目标值 - 无监督学习
    4.6.2 无监督学习包含算法
        聚类
        K-means(K均值聚类)
        降维
        PCA
    4.6.3 K-means原理
    4.6.5 案例：k-means对Instacart Market用户聚类
        k = 3
        流程分析：
        降维之后的数据
        1）预估器流程
        2）看结果
        3）模型评估
    4.6.6 Kmeans性能评估指标
        轮廓系数
        如果b_i>>a_i:趋近于1效果越好，
        b_i<<a_i:趋近于-1，效果不好。
        轮廓系数的值是介于 [-1,1] ，
        越趋近于1代表内聚度和分离度都相对较优。
    4.6.7 K-means总结
        应用场景：
            没有目标值
            分类
"""

 

相关代码：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
import joblib

def linear1():
    """
    正规方程的优化方法对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("正规方程-权重系数为：\n", estimator.coef_)
    print("正规方程-偏置为：\n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("正规方程-均方误差为：\n", error)

    return None

def linear2():
    """
    梯度下降的优化方法对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()
    # print("特征数量：\n", boston.data.shape)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000, penalty="l1")
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("梯度下降-权重系数为：\n", estimator.coef_)
    print("梯度下降-偏置为：\n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("梯度下降-均方误差为：\n", error)

    return None

def linear3():
    """
    岭回归对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()
    print("特征数量：\n", boston.data.shape)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    # estimator = Ridge(alpha=0.5, max_iter=10000)
    # estimator.fit(x_train, y_train)
    #
    # # 保存模型
    # joblib.dump(estimator, "my_ridge.pkl")
    # 加载模型
    estimator = joblib.load("my_ridge.pkl")

    # 5）得出模型
    print("岭回归-权重系数为：\n", estimator.coef_)
    print("岭回归-偏置为：\n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("岭回归-均方误差为：\n", error)

    return None

def linear3():
    """
    岭回归对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()
    print("特征数量：\n", boston.data.shape)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    # estimator = Ridge(alpha=0.5, max_iter=10000)
    # estimator.fit(x_train, y_train)
    #
    # # 保存模型
    # joblib.dump(estimator, "my_ridge.pkl")
    # 加载模型
    estimator = joblib.load("my_ridge.pkl")

    # 5）得出模型
    print("岭回归-权重系数为：\n", estimator.coef_)
    print("岭回归-偏置为：\n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("岭回归-均方误差为：\n", error)

    return None

实例

#%%

# 1、获取数据
# 2、合并表
# 3、找到user_id和aisle之间的关系
# 4、PCA降维

#%%

import pandas as pd

#%%

# 1、获取数据
order_products = pd.read_csv("./instacart/order_products__prior.csv")
products = pd.read_csv("./instacart/products.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")

#%%

# 2、合并表
# order_products__prior.csv：订单与商品信息

# 字段：order_id, product_id, add_to_cart_order, reordered
# products.csv：商品信息
# 字段：product_id, product_name, aisle_id, department_id
# orders.csv：用户的订单信息
# 字段：order_id,user_id,eval_set,order_number,….
# aisles.csv：商品所属具体物品类别
# 字段： aisle_id, aisle

# 合并aisles和products aisle和product_id
tab1 = pd.merge(aisles, products, on=["aisle_id", "aisle_id"])

#%%

tab2 = pd.merge(tab1, order_products, on=["product_id", "product_id"])

#%%

tab3 = pd.merge(tab2, orders, on=["order_id", "order_id"])

#%%

tab3.head()

#%%

# 3、找到user_id和aisle之间的关系
table = pd.crosstab(tab3["user_id"], tab3["aisle"])

#%%

data = table[:10000]

#%%

# 4、PCA降维
from sklearn.decomposition import PCA

#%%

# 1）实例化一个转换器类
transfer = PCA(n_components=0.95)

# 2）调用fit_transform
data_new = transfer.fit_transform(data)

#%%

data_new.shape

#%%

data_new

#%%

# 预估器流程
from sklearn.cluster import KMeans

#%%

estimator = KMeans(n_clusters=3)
estimator.fit(data_new)

#%%

y_predict = estimator.predict(data_new)

#%%

y_predict[:300]

#%%

# 模型评估-轮廓系数
from sklearn.metrics import silhouette_score

#%%

silhouette_score(data_new, y_predict)

#%%

#%%

import pandas as pd
import numpy as np

#%%

# 1、读取数据
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
column_name = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

data = pd.read_csv(path, names=column_name)

#%%

data.head()

#%%

# 2、缺失值处理
# 1）替换-》np.nan
data = data.replace(to_replace="?", value=np.nan)
# 2）删除缺失样本
data.dropna(inplace=True)

#%%

data.isnull().any() # 不存在缺失值

#%%

# 3、划分数据集
from sklearn.model_selection import train_test_split

#%%

data.head()

#%%

# 筛选特征值和目标值
x = data.iloc[:, 1:-1]
y = data["Class"]

#%%

x.head()

#%%

y.head()

#%%

x_train, x_test, y_train, y_test = train_test_split(x, y)

#%%

x_train.head()

#%%

# 4、标准化
from sklearn.preprocessing import StandardScaler

#%%

transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

#%%

x_train

#%%

from sklearn.linear_model import LogisticRegression

#%%

# 5、预估器流程
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

#%%

# 逻辑回归的模型参数：回归系数和偏置
estimator.coef_

#%%

estimator.intercept_

#%%

# 6、模型评估
# 方法1：直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)

# 方法2：计算准确率
score = estimator.score(x_test, y_test)
print("准确率为：\n", score)

#%%

# 查看精确率、召回率、F1-score
from sklearn.metrics import classification_report

#%%

report = classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"])

#%%

print(report)

#%%

y_test.head()

#%%

# y_true：每个样本的真实类别，必须为0(反例),1(正例)标记
# 将y_test 转换成 0 1
y_true = np.where(y_test > 3, 1, 0)

#%%

y_true

#%%

from sklearn.metrics import roc_auc_score

#%%

roc_auc_score(y_true, y_predict)

#%%