用 TensorFlow 实现 SVM 分类问题
这篇文章解释了底部链接的代码。
问题描述
 

如上图所示,有一些点位于单位正方形内,并做好了标记。要求找到一条线,作为分类的标准。这些点的数据在 inearly_separable_data.csv 文件内。
思路
最初的 SVM 可以形式化为如下:
\[\begin{equation}\min_{\boldsymbol{\omega,b}}\frac{1}{2}\|\boldsymbol{\omega}\|^2\\s.t.\ y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+b)\geqslant 1,\ i = 1,2,\cdots ,m.\end{equation} \]
引入软间隔,可以在一定情况下避免过拟合的问题。
引入软间隔之后,问题转化为
\[\begin{equation}
\min_{\boldsymbol{\omega,b}}\frac{1}{2}\|\boldsymbol{\omega}\|^2 + C \sum_{i=1}^{N}max(0,1-y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+b))
\end{equation}\]
代码
主要代码在 linear_svm.py 内,plot_boundary_on_data.py 负责画图。
一、引入库和声明
import tensorflow as tf
import numpy as np
import scipy.io as io
from matplotlib import pyplot as plt
import plot_boundary_on_data
二、 定义一些变量
# Global variables.
BATCH_SIZE = 100 # The number of training examples to use per training step.
# Define the flags useable from the command line.
tf.app.flags.DEFINE_string('train', None,
'File containing the training data (labels & features).')
tf.app.flags.DEFINE_integer('num_epochs', 1,
'Number of training epochs.')
tf.app.flags.DEFINE_float('svmC', 1,
'The C parameter of the SVM cost function.')
tf.app.flags.DEFINE_boolean('verbose', False, 'Produce verbose output.')
tf.app.flags.DEFINE_boolean('plot', True, 'Plot the final decision boundary on the data.')
FLAGS = tf.app.flags.FLAGS
包括每次训练使用的数据,称为一个 batch,大小定义为 BATCH_SIZE。
train 是训练集文件的位置,这里是 inearly_separable_data.csv。
num_epochs 是把所有训练集的数据使用几遍。把训练集的数据使用一遍称为一个 epoch。
svmC 即\((2)\)式中 \(C\)的大小。
三、读取训练数据
# Extract it into numpy matrices.
train_data,train_labels = extract_data(train_data_filename)
# Convert labels to +1,-1
train_labels[train_labels==0] = -1
# Get the shape of the training data.
train_size,num_features = train_data.shape
读出来的 train_data 是一个 [1000, 2] 的张量,样本的有两个属性,train_labels 是一个 [1000, 1] 的张量。
在读取过程中用到了 numpy 的接口。
标准的 SVM 的标记为 \(\{-1, 1\}\),而文件中标记为 \(\{0, 1\}\)。因此需要做一次转换。
四、构造网络结构
x = tf.placeholder("float", shape=[None, num_features])
y = tf.placeholder("float", shape=[None,1])
W = tf.Variable(tf.zeros([num_features,1]))
b = tf.Variable(tf.zeros([1]))
y_raw = tf.matmul(x,W) + b
线性方程的最终表现形式是 \(\boldsymbol{\omega}^t\boldsymbol{x}+b=0\)。
给定一个样本数据 \(\boldsymbol{x}\),若 \(\boldsymbol{\omega}^t\boldsymbol{x}+b \geqslant 1\),则认为对应的分类为 1,然后和样本的标记对比,若标记为1,则分类正确;否则,分类错误。
若 \(\boldsymbol{\omega}^t\boldsymbol{x}+b \leqslant 1\),则认为对应的分类为 -1,然后和样本的标记对比,若标记为-1,则分类正确;否则,分类错误。
最终要求解的值是一个 shape 为 [2, 1] 的张量 \(W\) 和一个标量 \(b\)。
y_raw 是向量机判定的输出。
五、构造优化目标
regularization_loss = 0.5*tf.reduce_sum(tf.square(W))
hinge_loss = tf.reduce_sum(tf.maximum(tf.zeros([BATCH_SIZE,1]),
1 - y*y_raw));
svm_loss = regularization_loss + svmC*hinge_loss;
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(svm_loss)
即 \( \min_{\boldsymbol{\omega,b}}\frac{1}{2}\|\boldsymbol{\omega}\|^2 + C \sum_{i=1}^{N}max(0,1-y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+b))\) 的代码表示。
指定用梯度下降法最小化 svm_loss。
六、用精度来评价模型的好坏
predicted_class = tf.sign(y_raw);
correct_prediction = tf.equal(y,predicted_class)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
如果 y_raw和样本的标记 y 同符号,即认为预测正确。用预测正确的比例来评价模型的好坏。
七、用数据训练模型
with tf.Session() as s:
# Run all the initializers to prepare the trainable parameters.
tf.initialize_all_variables().run()
# Iterate and train.
for step in xrange(num_epochs * train_size // BATCH_SIZE):
offset = (step * BATCH_SIZE) % train_size
batch_data = train_data[offset:(offset + BATCH_SIZE), :]
batch_labels = train_labels[offset:(offset + BATCH_SIZE)]
train_step.run(feed_dict={x: batch_data, y: batch_labels})
print 'loss: ', svm_loss.eval(feed_dict={x: batch_data, y: batch_labels})
首先启动一个 session,每次取 BATCH_SIZE 个数据来训练模型。即用batch_data 和 batch_lables来训练一次,每次得到一个 svm_loss 的值。
运行结果
python linear_svm.py --train linearly_separable_data.csv --svmC 1 --verbose True --num_epochs 10
运行以上命令,指定把数据使用10轮,一次使用100个数据,因此可以得到100次迭代的结果。最后得到的结果及精度如下:
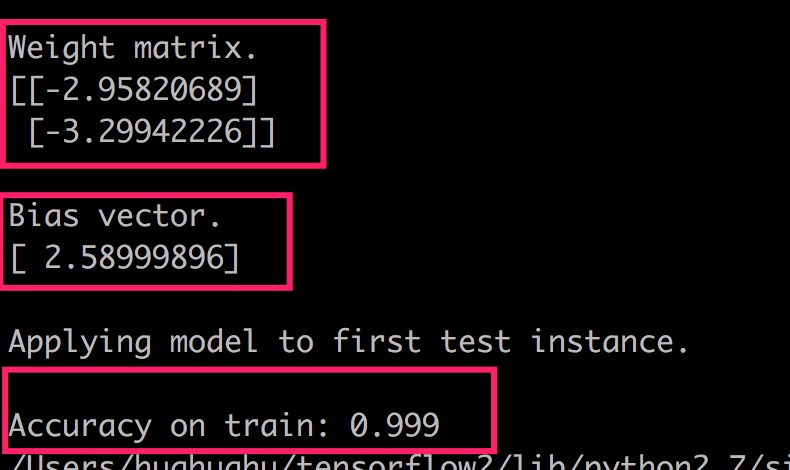 

思考
- 指定
BATCH_SIZE和num_epochs是为了减少计算量。
根据数学理论,应该在整个训练数据集上进行梯度下降法的迭代,每一步迭代都应该选取所有训练数据集的样本。但是这样子做计算量太大,于是在每一次迭代时选用训练数据集的一部分作为输入。
这么做要求每一步迭代选取的数据子集的分布和总体分布一致,否则得不到正确的结果。




