HDU - 6116：路径计数 （组合数&NTT）

一个包含四个点的完全图，可以在任意节点出发，可以在任意节点结束，给出每个点被经过的次数，求有多少种合法的遍历序列。如果两个序列至少有一位是不同的，则认为它们不相同。

Input

2 3 3 3

Sample Output

12336

题意：给a个A，b个B，c个C，d个D，求有少种排列，使得相邻的两个不同。

思路：用容斥来做，ans=所有排列-至少一个相邻+至少两个相邻-...+...。

假设有i堆a，则方案数位C(a-1,i-1)，则a中至少a-i个相邻；同理； 则i堆a，j堆b，k堆c，l堆d，至少有N-i-j-k-l个相邻，其对应的排列数为 N!/(i!*j!*k!*l!)；

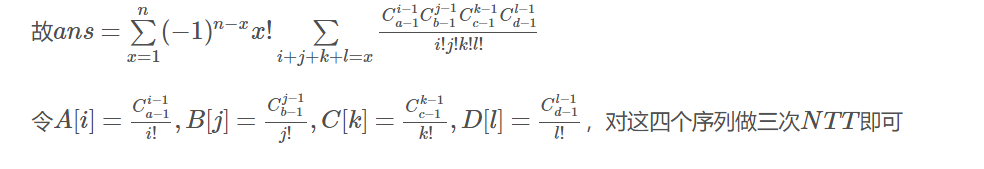
#include<bits/stdc++.h>
#define rep(i,x,y) for(int i=x;i<=y;i++)
using namespace std;
#define MOD Mod
#define ll long long
const int G=3;
const int Mod=998244353;
const int maxn=25764;
int qpow(int v,int p)
{
    int ans=1;
    for(;p;p>>=1,v=1ll*v*v%Mod)
      if(p&1)ans=1ll*ans*v%Mod;
    return ans;
}
void rader(int y[], int len) {
    for(int i=1,j=len/2;i<len-1;i++) {
        if(i<j) swap(y[i],y[j]);
        int k=len/2;
        while(j>=k) j-=k,k/=2;
        if(j<k) j+=k;
    }
}
void NTT(int y[],int len,int opt) {
    rader(y,len);
    for(int h=2;h<=len;h<<=1) {
        int wn=qpow(G,(MOD-1)/h);
        if(opt==-1) wn=qpow(wn,Mod-2);
        for(int j=0;j<len;j+=h) {
            int w=1;
            for(int k=j;k<j+h/2;k++) {
                int u=y[k];
                int t=(ll)w*y[k+h/2]%MOD;
                y[k]=(u+t)%MOD;
                y[k+h/2]=(u-t+MOD)%MOD;
                w=(ll)w*wn%MOD;
            }
        }
    }
    if(opt==-1) {
        int t=qpow(len,MOD-2);
        for(int i=0;i<len;i++) y[i]=(ll)y[i]*t%MOD;
    }
}
int A[maxn],B[maxn],C[maxn],D[maxn],f[maxn],rev[maxn],a,b,c,d;
int main()
{
    int N,K;
    f[0]=rev[0]=1;
    rep(i,1,4000) f[i]=(ll)f[i-1]*i%Mod;
    rev[4000]=qpow(f[4000],Mod-2);
    for(int i=3999;i>=1;i--) rev[i]=(ll)rev[i+1]*(i+1)%Mod;
    while(~scanf("%d%d%d%d",&a,&b,&c,&d)){
        N=a+b+c+d;
        memset(A,0,sizeof(A));
        memset(B,0,sizeof(B));
        memset(C,0,sizeof(C));
        memset(D,0,sizeof(D));
        rep(i,1,a) A[i]=(ll)f[a-1]*rev[i-1]%Mod*rev[a-i]%Mod*rev[i]%Mod;
        rep(i,1,b) B[i]=(ll)f[b-1]*rev[i-1]%Mod*rev[b-i]%Mod*rev[i]%Mod;
        rep(i,1,c) C[i]=(ll)f[c-1]*rev[i-1]%Mod*rev[c-i]%Mod*rev[i]%Mod;
        rep(i,1,d) D[i]=(ll)f[d-1]*rev[i-1]%Mod*rev[d-i]%Mod*rev[i]%Mod;
        int len=1; while(len<=N) len<<=1;
        NTT(A,len,1); NTT(B,len,1);
        rep(i,0,len-1) A[i]=(ll)A[i]*B[i]%Mod;

        NTT(C,len,1);
        rep(i,0,len-1) A[i]=(ll)A[i]*C[i]%Mod;

        NTT(D,len,1);
        rep(i,0,len-1) A[i]=(ll)A[i]*D[i]%Mod;
        NTT(A,len,-1);

        int opt,ans=0;
        if(N&1) opt=1; else opt=-1;
        rep(i,1,N) (((ans+=(ll)opt*f[i]*A[i]%Mod)%=Mod)+=Mod)%=Mod,opt=-opt;
        printf("%d\n",ans);
    }
    return 0;
}