【矩阵---求A的1到N次幂之和】

引例： Matrix Power Series：

题目大意，给定矩阵A，求A^1+A^2+A^3+...A^N。

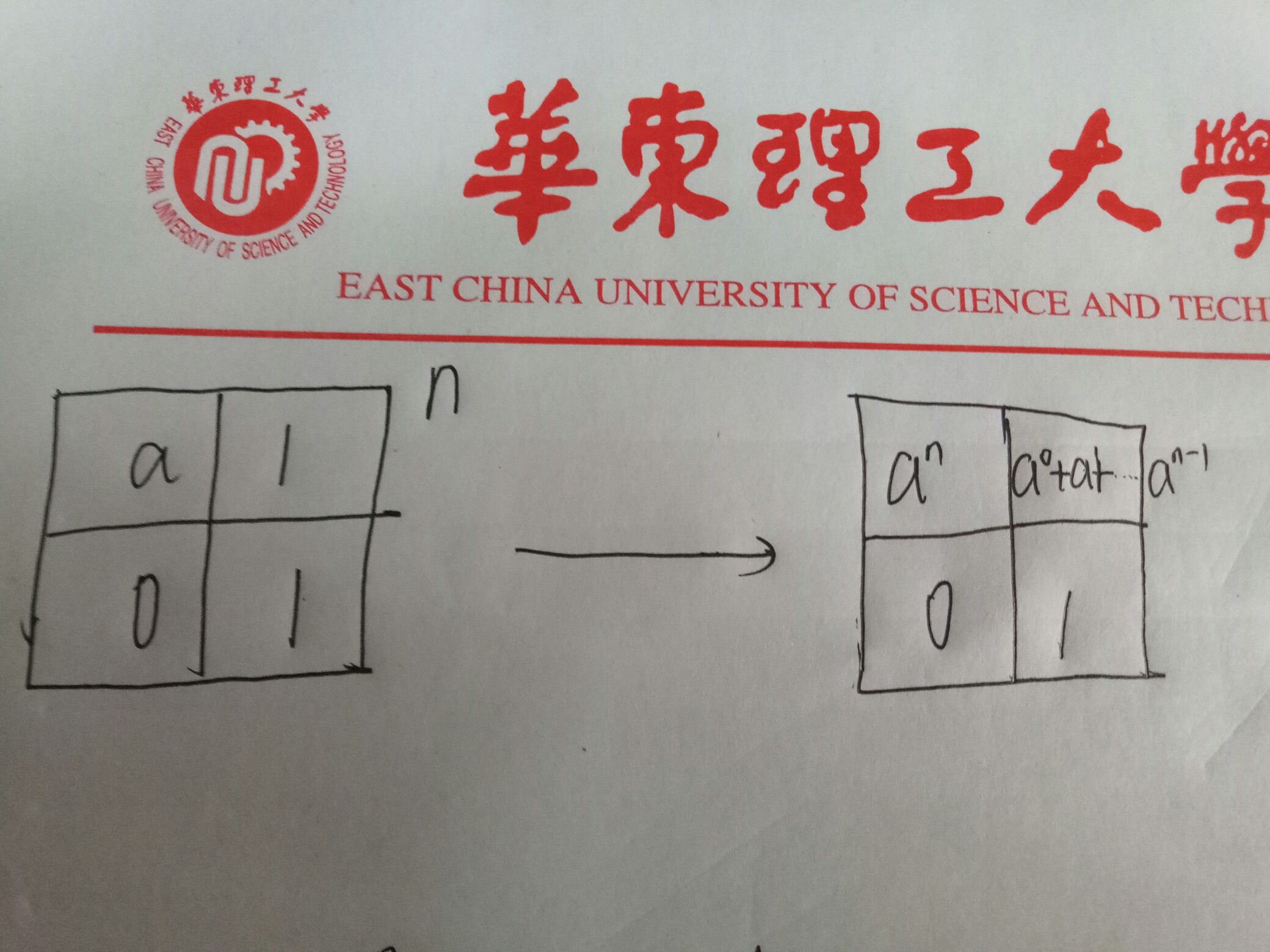
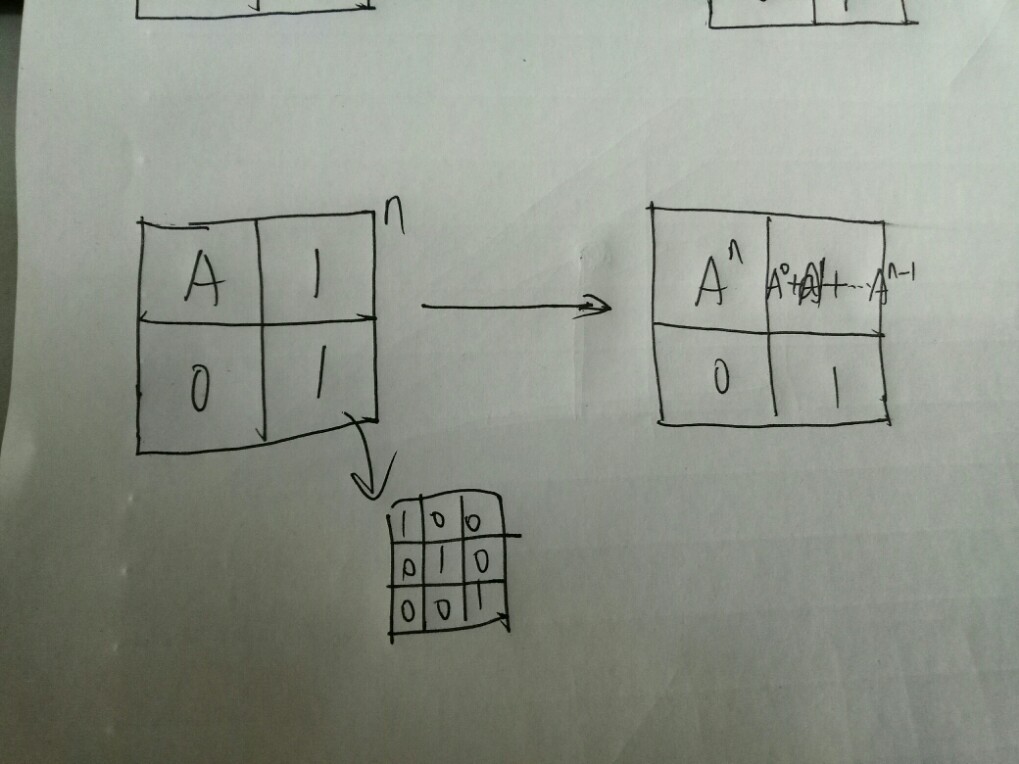
题解：已知X=a，可以通过以下矩阵求出ans=a^1+a^2+...a^N ans=矩阵^n后第一行之和-1=矩阵^(n+1)后右上格的和-1。

同理：矩阵也可以，只需要把1改为单位矩阵元即可。

左图a是常数，1就是1； 右图A是矩阵，1是单位元矩阵（主对角线是1）。

          

 

代码1：矩阵^N，第一行之和-1。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=70;
int N,K,Mod;
struct mat
{
    int mp[maxn][maxn],len;
    mat(int x){ len=x; memset(mp,0,sizeof(mp)); }
    mat friend operator *(mat a,mat b)
    {
        mat res(a.len);
        for(int k=1;k<=res.len;k++)
         for(int i=1;i<=res.len;i++)
          for(int j=1;j<=res.len;j++)
            res.mp[i][j]=(res.mp[i][j]+a.mp[i][k]*b.mp[k][j])%Mod;
        return res;
    }
    mat friend operator ^(mat a,int x)
    {
        mat res(a.len);
        for(int i=1;i<=res.len;i++) res.mp[i][i]=1;
        while(x){
            if(x&1)res=res*a;  a=a*a;  x>>=1;
        }   return res;
    }
};
int main()
{
    scanf("%d%d%d",&N,&K,&Mod);
    mat array(N+N);
    for(int i=1;i<=N;i++)
      for(int j=1;j<=N;j++){ 
         scanf("%d",&array.mp[i][j]);
    } 
    for(int i=1;i<=N;i++) array.mp[i][i+N]=array.mp[i+N][i+N]=1;
    array=array^(K);
    for(int i=1;i<=N;i++) array.mp[i][i+N]-=1;
    for(int i=1;i<=N;i++){
        for(int j=1;j<N;j++)
           printf("%d ",(array.mp[i][j]+array.mp[i][j+N]+Mod)%Mod);
        printf("%d\n",(array.mp[i][N]+array.mp[i][N+N]+Mod)%Mod);
    }
    return 0;
}

代码2：矩阵^N+1，右上格之和-1。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=70;
int N,K,Mod;
struct mat
{
    int mp[maxn][maxn],len;
    mat(int x){ len=x; memset(mp,0,sizeof(mp)); }
    mat friend operator *(mat a,mat b)
    {
        mat res(a.len);
        for(int k=1;k<=res.len;k++)
         for(int i=1;i<=res.len;i++)
          for(int j=1;j<=res.len;j++)
            res.mp[i][j]=(res.mp[i][j]+a.mp[i][k]*b.mp[k][j])%Mod;
        return res;
    }
    mat friend operator ^(mat a,int x)
    {
        mat res(a.len);
        for(int i=1;i<=res.len;i++) res.mp[i][i]=1;
        while(x){
            if(x&1)res=res*a;  a=a*a;  x>>=1;
        }   return res;
    }
};
int main()
{
    scanf("%d%d%d",&N,&K,&Mod);
    mat array(N+N);
    for(int i=1;i<=N;i++)
      for(int j=1;j<=N;j++){ 
         scanf("%d",&array.mp[i][j]);
    } 
    for(int i=1;i<=N;i++) array.mp[i][i+N]=array.mp[i+N][i+N]=1;
    array=array^(K+1);
    for(int i=1;i<=N;i++) array.mp[i][i+N]-=1;
    for(int i=1;i<=N;i++){
        for(int j=1;j<N;j++)
           printf("%d ",(array.mp[i][j+N]+Mod)%Mod);
        printf("%d\n",(array.mp[i][N+N]+Mod)%Mod);
    }
    return 0;
}

代码3：利用二分。

 

--------------------分界线---------------------------

 

例题：HDU2243：考研路茫茫——单词情结

题意：问长度位1到L的所有单词中，有多少个不含给出的几个单词。

思路：利用矩阵得到可以26的1到N次幂。然后利用AC自动机得到基本矩阵X，再利用矩阵得到得到X^0+X^1+X^2...X^N。
比如得到26的0到N次幂和，就有矩阵a[0][0]=26,a[0][1]=1,a[1][0]=0,a[1][1]=1;
矩阵^N后，第一行的和就是答案。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ull unsigned long long
const int maxn=40;
int ch[maxn][26],cnt;
int q[maxn],head,tail,Next[maxn],tag[maxn];
char s[20];
struct mat
{
    ull mp[maxn][maxn];
    mat(){memset(mp,0,sizeof(mp));}
    mat init(){ memset(mp,0,sizeof(mp));}
    mat friend operator *(mat a,mat b)
    {
        mat res;
        for(int k=0;k<=max(cnt,2);k++)
          for(int i=0;i<=max(cnt,2);i++)
            for(int j=0;j<=max(cnt,2);j++)
             res.mp[i][j]+=a.mp[i][k]*b.mp[k][j];
        return res;
    }
    mat friend operator ^(mat a,int x)
    {
        mat res; 
        for(int i=0;i<=cnt;i++) 
            res.mp[i][i]=1;
        while(x){
            if(x&1) res=res*a; 
            a=a*a; x>>=1;
        }   return res;
    }
};

mat array;

struct ACautom
{
    void update()
    {
        cnt=head=tail=0;
        memset(Next,0,sizeof(Next));
        memset(tag,0,sizeof(tag));
        memset(ch,0,sizeof(ch));
        array.init();
    }
    void insert()
    {
        int Now=0;
        for(int i=0;s[i];i++){
            int x=s[i]-'a';
            if(!ch[Now][x]) ch[Now][x]=++cnt;
            Now=ch[Now][x];
        } tag[Now]=1;
    }
    void build()
    {
        for(int i=0;i<26;i++){
            if(ch[0][i]) q[++head]=ch[0][i];    
            if(!tag[ch[0][i]]) array.mp[0][ch[0][i]]++;
        }
        while(tail<head){
            int u=q[++tail];
            for(int i=0;i<26;i++){
                if(ch[u][i]){
                    q[++head]=ch[u][i];
                    Next[ch[u][i]]=ch[Next[u]][i];
                    if(tag[Next[ch[u][i]]]) tag[ch[u][i]]=1;
                }
                else ch[u][i]=ch[Next[u]][i];
                if(!tag[ch[u][i]]) array.mp[u][ch[u][i]]++;
            }
        }
        cnt++;
        for(int i=0;i<=cnt;i++) array.mp[i][cnt]=1;
    }
    void qpow(int K)
    {
        ull ans,res=0;
        mat base;
        base.mp[0][0]=26; base.mp[0][1]=1;
        base.mp[1][0]=0;  base.mp[1][1]=1;
        base=base^K;
        ans=base.mp[0][0]+base.mp[0][1];
        array=array^K;
        for(int i=0;i<=cnt;i++) res=res+array.mp[0][i];
        cout<<ans-res<<endl;
    }
}Trie;
int main()
{
    int N,K;
    while(~scanf("%d%d",&N,&K)){
        Trie.update();
        for(int i=1;i<=N;i++) {
            scanf("%s",s);
            Trie.insert();
        }
        Trie.build();
        Trie.qpow(K);
    }
    return 0;
}