考研系列 HDU2241之早起看书 三分

考研并不是说说就可以了，要付诸于行动。 

对于Lele来说，最痛苦的事莫过于早起看书了，不过为了考研，也就豁出去了。由于早起看书会对看书效率产生影响，所以对于要什么时候起床看书，还是有必要考虑的。 

经过周密的调查，Lele发现早起的时间会对上午和下午的看书效率都产生影响，具体如下： 

他把早起的程度标记为一个非负有理数X，X数值越大，表示越早起。 

1.对上午的影响F：符合 F = N / (X^2) 。其中N是一个参数。即越早起床，对上午的效率影响越少。 

2.对下午的影响Y：一般越早起，对下午的效率影响越大。不过Y和X的关系比较复杂，并且在不同时候关系也是不同的，于是Lele把它绘制成为函数图形了。在某天，函数图形如下。 



X轴的值表示早起的程度，Y轴的值表示对下午看书效率的影响。函数图像为折线上升的。 

不过由于N值和Y-X的图像并不确定，所以Lele每次都要进行大量工作，来确保对整天的看书效率影响最小(F+Y的值最小)，现在就请你帮帮他吧。 

记住早起时间的取值X一定要在折线包含的范围之内。(对于上面这个图象，X一定要在[0,20]之内)。 

Input本题目包含多组输入，请处理到文件结束。 
每组测试第一行包含两个整数M和N(1<M<10000,0<=N<=2^31)。其中M表示X-Y图像中顶点的数目。N含义见题目描述。 
接下来有M行整数，分别表示这M个点在图像中的坐标Xi和Yi，Xi和Yi范围在[0,2^30]之内。 

注意，第一个坐标一定为(0,0)，并且X坐标和Y坐标是不降的，即对于任意 i<j Xi<Xj 且 Yi<=Yj。 

而Lele早起的时间一定在[0,Xm-1]这个范围之内。Output对于每组数据，请在一行内输出可能取到的对全天效率(Y+F)影响的最小值。 
结果保留三位小数Sample Input

3 1
0 0
10 10
20 30
2 1000
0 0
10 10

Sample Output

1.890
20.000

一开始用不等式的极值来解决，但是不知道怎么取精度，所以必WA。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<memory>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
double n,m,j;
int i;
double ans,prex,prey,nowx,nowy;
double k,b,tmp,tx;
int main()
{
    while(~scanf("%lf%lf",&m,&n)){
        scanf("%lf%lf",&prex,&prey);
        ans=1e100;
        for(i=2;i<=m;i++){
            scanf("%lf%lf",&nowx,&nowy);
            k=(nowy-prey)/(nowx-prex); 
            b=nowy-k*nowx;
            if(i==2) ans=n/(nowx*nowx)+nowy;
            else  ans=min(ans,n/(nowx*nowx)+nowy);
            tmp=3*pow(1.0*n*k*k/4,(double)1.0/3);
            tx=pow(1.0*2*n/k,(double)1.0/3);
            if(tx>prex&&tx<=nowx) ans=min(n/(tx*tx)+k*tx+b,ans);
            prex=nowx;prey=nowy;
        }
        printf("%.3lf\n",ans);
    }
    return 0;
}

 

然后想着用二分来逼近这个0.0001的精度，但是极值点处直接二分显然是错误的。

如图，我们在L1到L4之间取逼近这个答案，二分的话会迷。但是用L2和L3三分，可以得到如下结论：

      A，B中选值大的一个一直沿着值小的方向走到边界，会路过极值点，比如此图，y2(A)>y3(B)，从A走到L4，会经过极值点C。极小值点不可能在O-A之间，因为A的右边存在B<A。那么极小值C的位置无非两种情况，C点可能在L2到L3之间，或者L3到L4之间。在L2到L3之间的话，说明极值点在A，B间，显然会遇到极值点。在L3到L4之间的话，说明A-B单调递减，继续延伸，显然也会遇到极小值点。证明结束。

 

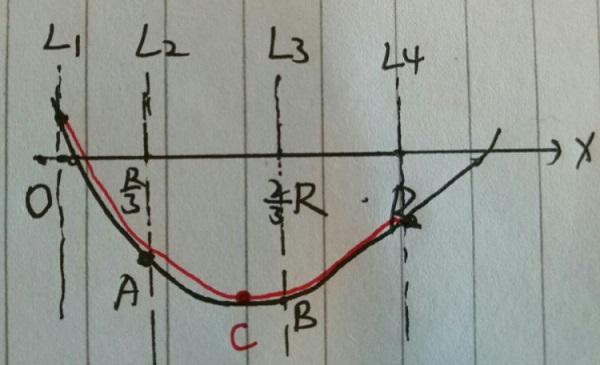
其次，保留三位有效数字，则精确到R-L<0.0001，即可完成三分。但是任然有细节需要注意，毕竟精度很容易出错！QWQ

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<memory>
#include<cstring>
#include<algorithm>
#include<cmath>
#define eps 1e-4
using namespace std;
int n,m,i,prex,prey,nowx,nowy;
double k,d,L,R,tmp1,tmp2,ans;
int main()
{
    while(scanf("%d%d",&m,&n)!=EOF){
        scanf("%d%d",&prex,&prey);//输入0，0 
        ans=1e100;//最大 
        for(i=2;i<=m;i++){
            scanf("%d%d",&nowx,&nowy);
            k=(0.0+nowy-prey)/(0.0+nowx-prex); //斜率k-->y=kx+b 
            L=prex;R=nowx;
            while(R-L>eps)
            {
                d=(R-L)/3;
                tmp1=n/((L+d)*(L+d))+k*(L+d);
                tmp2=n/((R-d)*(R-d))+k*(R-d);
                if(tmp1<=tmp2) R=R-(R-L)/3;
                else L=L+(R-L)/3;
            }
            d=(R-L)/3;//细节 
            tmp1=n/(((L+d)*(L+d)))+k*(L+d)+nowy-k*nowx;//不是L 
            if(ans>tmp1) ans=tmp1;
            prex=nowx;prey=nowy;//替换 
        }
        printf("%.3lf\n",ans);
    }
    return 0;
}