实现二叉排序树的各种算法
实现二叉排序树的各种算法
Description
用函数实现如下二叉排序树算法: (1) 插入新结点 (2) 前序、中序、后序遍历二叉树 (3) 中序遍历的非递归算法 (4) 层次遍历二叉树 (5) 在二叉树中查找给定关键字(函数返回值为成功1,失败0) (6) 交换各结点的左右子树 (7) 求二叉树的深度 (8) 叶子结点数
Input
第一行:准备建树的结点个数n 第二行:输入n个整数,用空格分隔 第三行:输入待查找的关键字 第四行:输入待查找的关键字 第五行:输入待插入的关键字
Output
第一行:二叉树的先序遍历序列 第二行:二叉树的中序遍历序列 第三行:二叉树的后序遍历序列 第四行:查找结果 第五行:查找结果 第六行~第八行:插入新结点后的二叉树的先、中、序遍历序列 第九行:插入新结点后的二叉树的中序遍历序列(非递归算法) 第十行:插入新结点后的二叉树的层次遍历序列 第十一行~第十三行:第一次交换各结点的左右子树后的先、中、后序遍历序列 第十四行~第十六行:第二次交换各结点的左右子树后的先、中、后序遍历序列 第十七行:二叉树的深度 第十八行:叶子结点数
Sample Input
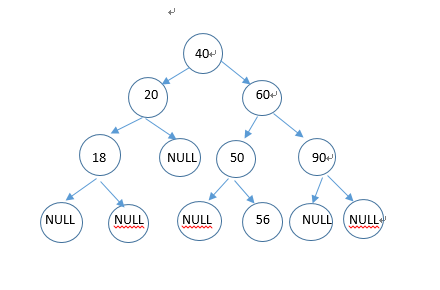
7 40 20 60 18 50 56 90 18 35 30
Sample Output
40 20 18 60 50 56 90
18 20 40 50 56 60 90 18 20 56 50 90 60 40 1 0 40 20 18 30 60 50 56 90 18 20 30 40 50 56 60 90 18 30 20 56 50 90 60 40 18 20 30 40 50 56 60 90 40 20 60 18 30 50 90 56 40 60 90 50 56 20 30 18 90 60 56 50 40 30 20 18 90 56 50 60 30 18 20 40 40 20 18 30 60 50 56 90 18 20 30 40 50 56 60 90 18 30 20 56 50 90 60 40 4 4
//以下为AC代码
#include<stdio.h>
#include<stdlib.h>
#define OK 1
#define ERROR 0
#define Maxsize 100
typedef int TElemType;
typedef int status;
typedef struct BTree
{
TElemType data;
struct BTree *lchild,*rchild;
}BTnode,*BTpoint;
typedef struct stack
{
BTpoint *base,*top;
int stacksize;
}Stack;
typedef struct quence
{
BTpoint *front,*rear;
int quencesize;
}Quence;
status Creat_stack(Stack &S)
{
if(!(S.base=(BTpoint *)malloc(Maxsize * sizeof(BTpoint)))) return ERROR;
S.top=S.base;
S.stacksize=Maxsize;
return OK;
}
status Creat_quence(Quence &Q)
{
if(!(Q.front = (BTpoint *)malloc(Maxsize * sizeof(BTpoint)))) return ERROR;
Q.rear=Q.front;
Q.quencesize=Maxsize;
return OK;
}
status Creat_and_insert(BTpoint &T,TElemType x)//创建树和插入结点
{
if(T == NULL)
{
if(!(T = (BTpoint)malloc(sizeof(BTnode)))) return ERROR;
else
{
T->data = x;
T->lchild = T->rchild = NULL;
}
}
else
{
if(x<T->data)
return Creat_and_insert(T->lchild,x);
else return Creat_and_insert(T->rchild,x);
}
return OK;
}
status Print_tree_data(TElemType e)//打印数据
{
printf("%d ",e);
return OK;
}
status Firt_view_root(BTpoint T,status (*view)(TElemType e)) //先序遍历
{
if(T!=NULL)
{
if(Print_tree_data(T->data))
if(Firt_view_root(T->lchild,view))
if(Firt_view_root(T->rchild,view)) return OK;
return ERROR;
}
else return OK;
}
status Mid_view_root(BTpoint T,status (*view)(TElemType e)) //中序遍历
{
if(T!=NULL)
{
if(Mid_view_root(T->lchild,view))
if(Print_tree_data(T->data))
if(Mid_view_root(T->rchild,view)) return OK;
return ERROR;
}
else return OK;
}
status Last_view_root(BTpoint T,status (*view)(TElemType e)) //后序遍历
{
if(T!=NULL)
{
if(Last_view_root(T->lchild,view))
if(Last_view_root(T->rchild,view))
if(Print_tree_data(T->data)) return OK;
return ERROR;
}
else return OK;
}
status Find_data(BTpoint T,TElemType findit) //查找
{
if(T!=NULL)
{
if(findit == T->data) return 1;
else if(findit < T->data) return Find_data(T->lchild,findit);
else return Find_data(T->rchild,findit);
}
else return 0;
}
void viewall(BTpoint T,status (*view)(TElemType e))
{
Firt_view_root(T,Print_tree_data);
printf("\n");
Mid_view_root(T,Print_tree_data);
printf("\n");
Last_view_root(T,Print_tree_data);
printf("\n");
}
status M_nonrecursive(BTpoint T,Stack S) //中序遍历序列(非递归算法)
{
while(T!=NULL||S.base!=S.top)
{
while(T!=NULL)
{
*S.top++=T;
T=T->lchild;
}
T=*--S.top;
Print_tree_data(T->data);
T=T->rchild;
}
return OK;
}
status Level_view(BTpoint T,Quence Q) //层次遍历
{
if(T!=NULL)
{
*Q.rear++=T;
while(Q.front!=Q.rear)
{
if(T->lchild!=NULL) *Q.rear++=T->lchild;
if(T->rchild!=NULL) *Q.rear++=T->rchild;
T=*Q.front++;
printf("%d ",T->data);
T=*Q.front;
}
}
return OK;
}
status swap_tree(BTpoint &T)
{
BTpoint temp;
if(T!=NULL)
{
temp = T->lchild;
T->lchild = T->rchild;
T->rchild = temp;
swap_tree(T->lchild);
swap_tree(T->rchild);
}
return OK;
}
status tree_deep(BTpoint T) //求二叉树深度
{
int ld=0,rd=0;
if(T!=NULL)
{
ld = tree_deep(T->lchild);
rd = tree_deep(T->rchild);
}
else return 0;
return ld>rd?ld+1:rd+1;
}
status leaf_number(BTpoint T,int &num) //求叶子总数
{
if(T)
{
if(T->rchild==NULL && T->lchild==NULL) num++;
else
{
leaf_number(T->lchild,num);
leaf_number(T->rchild,num);
}
}
return OK;
}
int main()
{
BTpoint BT=NULL;
Stack S;
Quence Q;
int n,i,fnb1,fnb2,isnb;
int num=0,deep;
int a[Maxsize];
scanf("%d",&n); //第一行:输入准备建树的结点个数n
for(i=0;i<n;i++) //第二行:输入n个整数,用空格分隔
{
scanf("%d",&a[i]);
Creat_and_insert(BT,a[i]);
}
scanf("%d",&fnb1); //第三行:输入待查找的关键字
scanf("%d",&fnb2); //第四行:输入待查找的关键字
scanf("%d",&isnb); //第五行:输入待插入的关键字
viewall(BT,Print_tree_data);
printf("%d\n",Find_data(BT,fnb1));
printf("%d\n",Find_data(BT,fnb2));
//插入和插入后
Creat_and_insert(BT,isnb);
viewall(BT,Print_tree_data);
//第9和第10行的输出
Creat_stack(S);
M_nonrecursive(BT,S);
printf("\n");
Creat_quence(Q);
Level_view(BT,Q);
printf("\n");
//第一次交换
swap_tree(BT);
//第11~13行:第一次交换各结点的左右子树后的先、中、后序遍历序列
viewall(BT,Print_tree_data);
//第二次交换
swap_tree(BT);
//第14~16行:第二次交换各结点的左右子树后的先、中、后序遍历序列
viewall(BT,Print_tree_data);
//第17行,二叉树的深度
deep = tree_deep(BT);
printf("%d\n",deep);
//第18行,叶子结点总数
leaf_number(BT,num);
printf("%d\n",num);
return 0;
}





