C语言----二进制（基础篇十二）
......
位（bit）
在计算机内部，开关导通时，表示1；断开表示0。这样，电压不稳时计算机还能照样工作。
一个通断开关叫做一个“位”。
字节（byte）
计算机内部经常把8个位作为一组，用来表示许多我们平时生活中用到的东西。如：
00000000表示事物为假，11111111表示为真（非0即为真）
00000000表示数字0，00000011表示3
8个位可以表示不同的组合情况，比如音乐音符，颜色，这样就实现了多媒体。
全世界统一把8个位叫做一个“字节”，我们平时所说的硬盘容量、内存大小、U盘大小，都是以字节为单位。网络却经常使用位为单位，所以我们平时的上网速度要除以8（加上衰耗，实际上要除以10），才是下载速度。
二进制与整数
人类平时使用的数字都是逢十进一，叫十进制。在计算机中是逢二进一，叫二进制。
二进制表示成八进制和十六进制更加方便。八进制是逢八进一，用0到7表示。十六进制是逢十六进一，大于9的数字用字母A到F表示。
用八进制和十六进制表示二进制的原因是：3个位刚好是八进制的一位数，4个位刚好是十六进制的一位数。黑客和病毒工作者就经常工作在十六进制数上。
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
注：标黑体字的为关键数，关键数后面的数字，可从此关键数开始推导
※1个八进制位刚好是3个二进制位
※1个十六进制位刚好是4个二进制位。
※1个字节刚好是2个十六进制位
如：11111111刚好是FF
C语言中的八进制和十六进制
程序1
输入和输出十、八、十六进制
//12-1,输出十六进制，八进制 #include <stdio.h> main() { int i8, i10, i16; //八进制，十进制，十六进制 i8 = 015; //八进制的形式赋值 i10 = 15; //十进制的形式赋值 i16 = 0x15; //十六进制的形式赋值 printf("i8的输出形式%o,十进制为%d,十六进制为%x\n", i8, i8, i8); printf("i10的输出形式%o,十进制为%d,十六进制为%x\n", i10, i10, i10); printf("i16的输出形式%o,十进制为%d,十六进制为%x\n", i16, i16, i16); }
从程序中可以看出：
※整数前加个0，表示8进制常量，如：063
※整数前加个0x，表示16进制常量，如：0x3F
注意：C语言中没有二进制的输入输出，用库函数itoa也只能将十进制转换成二进制，二进制转十进制没有对应的库函数。
※八进制和十六进制整数没有负数。
各类型所占内存
| 类型 | 字节 | 类型 | 字节 |
|---|---|---|---|
| char | 1 | float | 4 |
| short | 2 | double | 8 |
| int | 4 | long double | 8 |
| long | 4 | 指针 | 4 |
※整型前加unsigned，所占字节数保持不变
※用sizeof可以计算出所有类型所占的字节数。
浮点数据类型因为在后面调出几位用来做指数部分，计算方法较复杂，本书作为入门丛书，不对此内容深入讲解。
进制转换
书写格式：
(数字)进制
如：
(111)2 (10)8 (FF)16
※十进制转二进制：用“除2取余法”
(20)10=(?)2
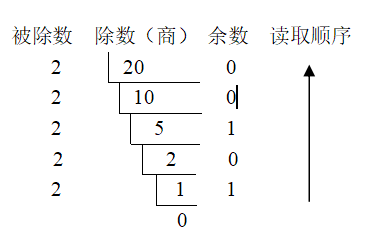
注意：要除到商为0为止
答案：(20)10=(10100)2
规律：以此类推，十进制转八进制可用“除8取余法”；转十六进制可用“除16取余法”
※二进制转十进制：用降幂法
(10100)2= (?)10
1*24+0*23+1*22+0*21+0*20=20
注意：任何数的0次幂等于1
(10100)2= (20)10
规律：八或十六进制转十进制只要将底数改为8或16即可
※二进制转八进制：
将二进制由低位到高位，3个分为1组，每组查表所得的八进制组合，就是最终结果。
(10,100)2= (24)8
※二进制转十六进制：
将二进制由低位到高位，4个分为1组，每组查表所得的十六进制组合，就是最终结果。
(1,0100)2= (14)16
※八和十六进制互转：
可以通过二进制作为中间进制，再转成另一个进制
※进制转换可以用Windows自带的计算器设置成科学型后再进行验算。
单位关系
数学中的单位关系：
太（T）、吉（G）、兆（M）、千（K）、字节（byte）、位（bit）
1T=1000G
1G=1000M
1M=1000K
1K=1000byte
1byte=8bit
计算机中的单位关系：
计算机中的单位关系都是1024，因为210=1024，便于计算机的计算，所以以上的单位关系应改为：
1T=1024G
1G=1024M
1M=1024K
1K=1024byte
1byte=8bit
