树和二叉树
树
二叉树
基本概念
二叉树是一个有限的结点集合,该集合或者为空,或者由一个根结点及其两棵互不相交的左、右二叉子树所组成。
二叉树的结点中有两棵子二叉树,分别称为左子树和右子树。因为二叉树可以为空,所以二叉树中的结点可能没有子结点,也可能只有一个左子结点(右子结点),也可能同时有左右两个子结点。
如图1-4所示是二叉树的4种可能形态(如果把空树计算在内,则共有5种形态)。
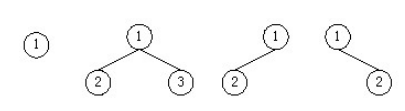
图1-4 二叉树的4种不同形态
与树相比,二叉树可以为空,空的二叉树没有结点(树至少有一个结点)。在二叉树中,结点的子树是有序的,分左、右两棵子二叉树。
二叉树常采用类似树的标准存储结构来存储,其结点类型可以用C语言定义如下:
typedef struct Btnode{ char data; /*数据*/ strucrt Btnode *lchild; /*左孩子*/ struct Btnode *rchild; /*右孩子*/ }BTNODE;
性质
性质1:在二叉树的第 i 层上至多有2i-1 个结点(i≥1)。
性质2:深度为 k 的二叉树至多有2k –1个结点(k≥1)。
性质3:对任何一棵二叉树,如果其叶子结点数为n0 ,度为2的结点数为n2 ,则 n0 = n2 +1。
证明,总结点数 n=n0+n1+n2, 另一方面,除了根节点,每一个节点上面都有一根线,故 n = B +1,度为1的有一根线,度为2的有两根线,故 n = n1 + 2n2 + 1
所以,n0+n1+n2 = n1 + 2n2 + 1 ,化简得 n0 = n2 +1
一棵深度为k且有2k –1(k≥1)个结点的二叉树称为满二叉树。如图1-5所示就是一棵满二叉树,对结点进行了顺序编号
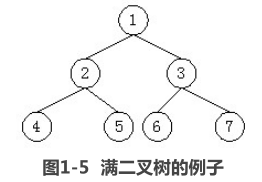
如果深度为k、有n个结点的二叉树中各结点能够与深度为k的顺序编号的满二叉树从1到n标号的结点相对应,则称这样的二叉树为完全二叉树。
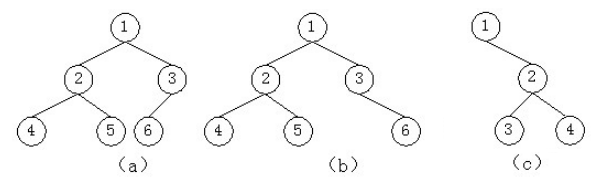
如图1-6(a)所示是一棵完全二叉树,而(b)、(c)是两棵非完全二叉树。显然,满二叉树是完全二叉树的特例。
性质4:具有n(n>0)个结点的完全二叉树的深度为 ⌊ log2n 」+1。(注: 符号⌊⌋为向下取整运算符, ⌈⌉为向上取整运算符, 表示不大于m的最大整数,反之, 表示不小于m的最小整数)
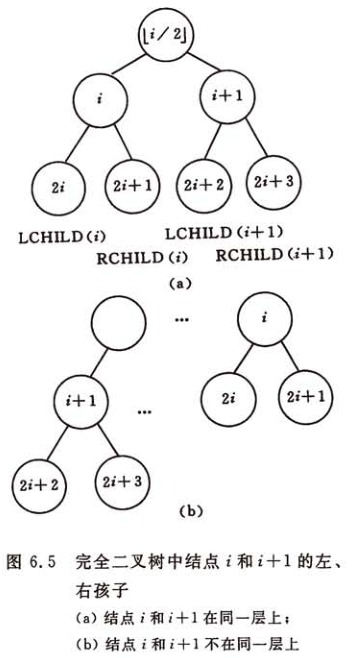
性质5:如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到第 L log 2 n」+1层,每层从左到右),则对任一结点 i(1≤i≤n),有:
如果i=1,则结点i无双亲,是二叉树的根;如果i>1,则其双亲是结点 ⌊ i/2 ⌋。
如果 2i > n,则结点i为叶子结点,无左孩子;否则,其左孩子是结点 2i 。
如果 2i+1 > n,则结点i无右孩子;否则,其右孩子是结点 2i+1。
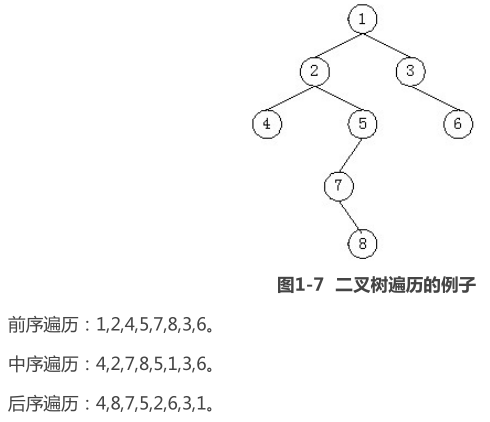
遍历
① NLR:前序遍历(Preorder Traversal 亦称(先序遍历))
——访问根结点的操作发生在遍历其左右子树之前。
② LNR:中序遍历(Inorder Traversal)
——访问根结点的操作发生在遍历其左右子树之中(间)。
③ LRN:后序遍历(Postorder Traversal)
——访问根结点的操作发生在遍历其左右子树之后。
注意:
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
性质6:一棵二叉树的前序序列和中序序列可以唯一地确定这棵二叉树。
给出中序遍历之后再给一个其他的遍历就能够确定了,前序和后序不能确定,因为一个根在最前,一个根在最后,无法区分左右孩子,不能递归的将孩子分开。
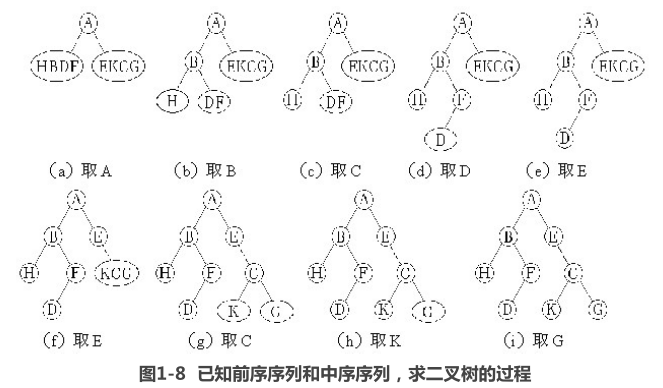
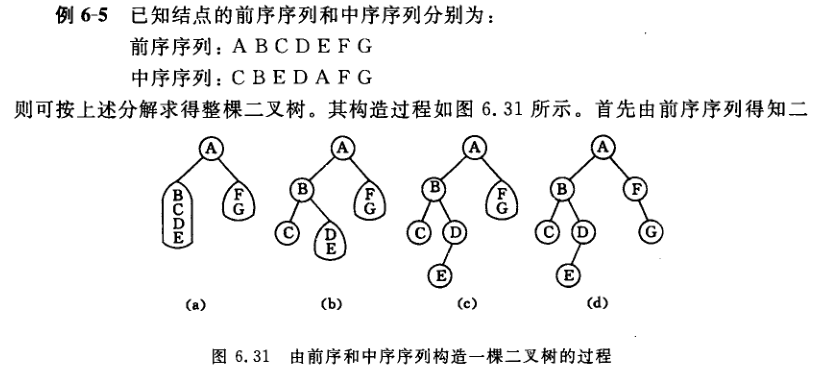
例如,给定一棵二叉树的前序序列和中序序列,我们可以写出该二叉树的后序序列。例如,某二叉树的前序序列为 ABHFDECKG,中序序列为HBDFAEKCG,则构造二叉树的过程如图1-8所示。
满二叉树
深度为k的二叉树拥有2k-1个结点,就称其为满二叉树。
完全二叉树
深度为k,具有n个结点的二叉树能与深度为k的满二叉树从编号1至n的结点都满足一一对应时,就称其为完全二叉树。
二叉排序树(BST)
二叉排序树又称为二叉查找树,其定义为二叉排序树或者是一棵空二叉树,或者是具有如下性质(BST性质)的二叉树:
(1)若它的左子树非空,则左子树上所有结点的值均小于根结点;
(2)若它的右左子树非空,则右子树上所有结点的值均大于根结点;
(3)左、右子树本身又各是一棵二叉排序树。
例如,如图1-9所示就是一棵二叉排序树。
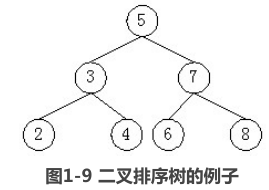
根据二叉排序树的定义可知,如果中序遍历二叉排序树,就能得到一个排好序的结点序列。二叉排序树上有查找、插入和删除等3种操作。下面,我们假设二叉排序树的结点只存储结点的键值,其类型与前面的二叉树的结点类型相同。
平衡二叉树
平衡二叉树也叫AVL树,它或者是一颗空树,或者具有以下性质的二叉排序树:它的左子树和左子树的高度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。(任意的子树的左右高度差不超过1)
平衡二叉排序树
构造平衡二叉排序树的方法,即在逐点插入法建立二又排序树的过程中,如果插入任意一个结点后,出现原来二叉排序树不平衡的情况,那么就需要对当前二叉排序树进行局部调整。
右旋:
https://img-blog.csdn.net/20180722222413303
左旋:
https://img-blog.csdn.net/20180722220546910
1. LL型调整
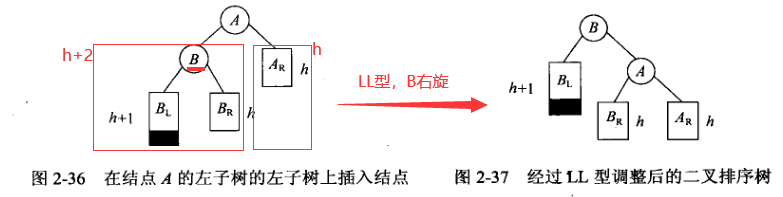
特别地:
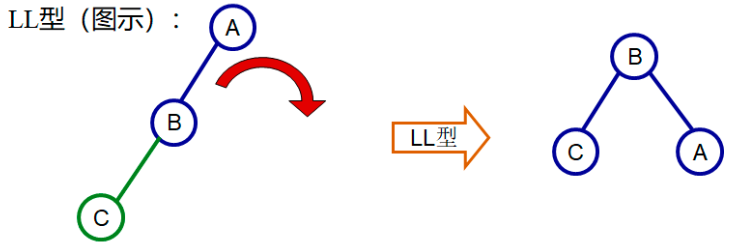
2. RR型调整
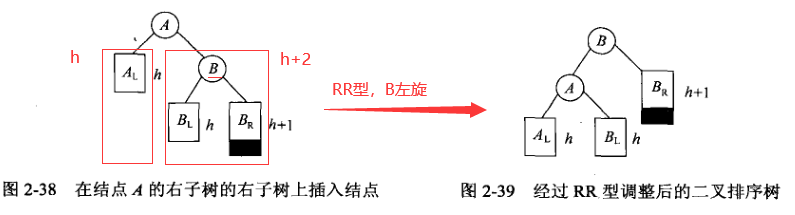
特别的:
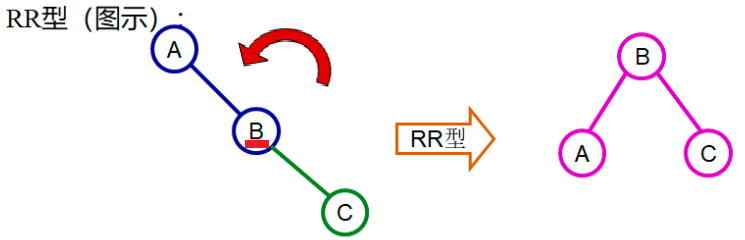
3. LR型调整
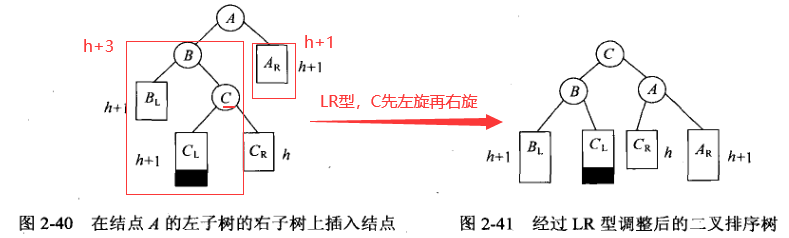
特别地:

4. RL型调整
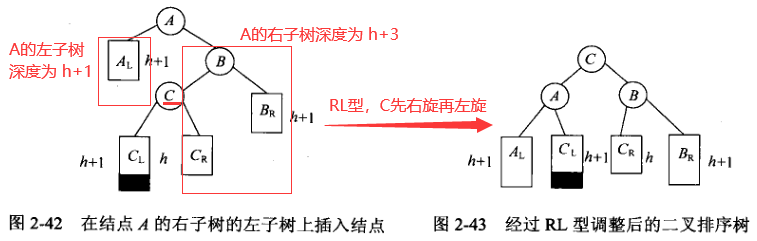
特别地:

哈夫曼树
哈夫曼树,又称最优树,是指带权重路径长度(WPL值)最小的树。
哈夫曼树的构造方法:

又 哈夫曼树是二叉树,故 n0 = n2 +1,所以 总结点数 n=2n2+1=2n0-1

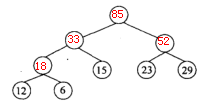
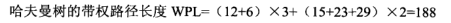
..
常记溪亭日暮,沉醉不知归路。兴尽晚回舟,误入藕花深处。争渡,争渡,惊起一滩鸥鹭。
昨夜雨疏风骤,浓睡不消残酒。试问卷帘人,却道海棠依旧。知否?知否?应是绿肥红瘦。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号