大话数据结构的读后感

一、算法效率的度量

最终，在分析程序的运行时间时，最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。

在分析一个算法的运行时间时，重要的是把基本操作的数量与输入规模关联起来，即基本操作的数量必须表示成输入规模的函数。
例如 f(n) = 2n+1, ...

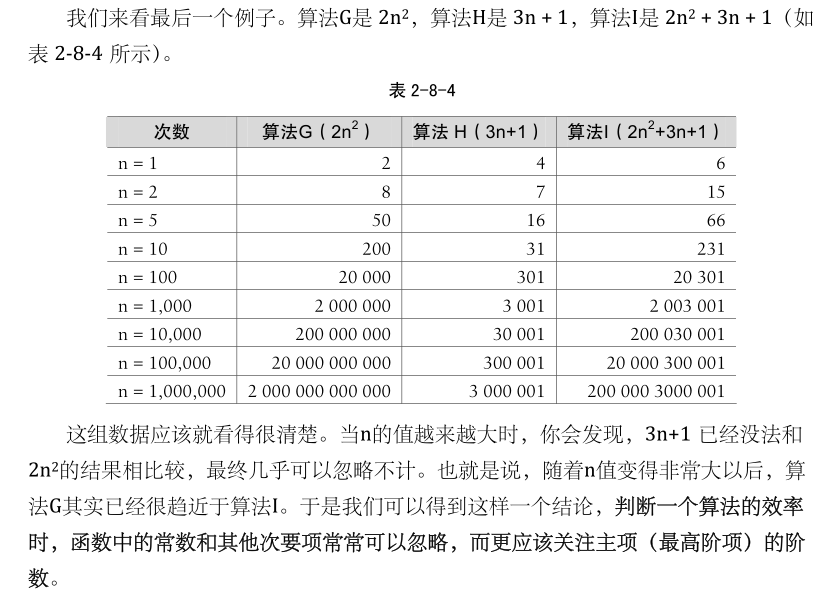
判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数。

这个结论，可以用极限的思维：

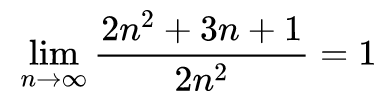
说明，n很大时分子和分母等价哦。

算法时间复杂度

算法时间复杂度定义

在进行算法分析时，语句总的执行次数 T（n）是关于问题规模 n 的函数，进而分析 T（n）随 n 的变化情况并确定 T（n）的数量级。
算法的时间复杂度，也就是算法的时间量度，记作：T（n）= O(f(n))。
它表示随问题规模 n 的增大，算法执行时间的增长率和f（n）的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。
其中 f（n）是问题规模 n 的某个函数。

这样用大写 O( )来体现算法时间复杂度的记法，我们称之为大O 记法。

一般情况下，随着n的增大，T(n) 增长最慢的算法为最优算法。

推导大O阶方法