深入理解计算机系统(2.4)---C语言的有符号与无符号、二进制整数的扩展与截断
本文转载地址:http://www.cnblogs.com/zuoxiaolong/p/computer8.html
在上一章中,我们着重介绍了整数的表示方式,也就是无符号编码和补码编码。本次我们来看一下二进制整数的扩展与截断,这部分内容是与C语言挂钩介绍的。因此我们首先来简单的看一下C语言的有符号数和无符号数。
C语言中的有符号数和无符号数
有符号数和无符号数的本质区别其实就是采用的编码不同,前者采用补码编码,后者采用无符号编码。
在C语言中,有符号数和无符号数是可以隐式转换的,不需要手动实施强制类型转换。不过也正是因为如此,可能你不小心将一个无符号数赋给了有符号数,就会造成出乎意料的结果,就像下面这样。
#include <stdio.h>
int main(){
short i = -12345;
unsigned short u = i;
printf("%d %d\n",i,u);
}
结果如下。

一个不小心,一个负数就变成正数了,再看下面这个程序,它展示了在进行关系运算时,由于有符号数和无符号数的隐式转换所导致的违背常规的结果。
#include <stdio.h>
int main(){
printf("%d\n",-1 < 0U);
printf("%d\n",-12345 < 12345U);
}
结果如下。
可以看到,两个结果都为0,也就是false,这与我们直观的理解是违背的,原因就是因为在比较的过程中,有符号数被隐式的转换成了无符号数进行比较。
扩展
当我们将一个短整型的变量转换为整型变量时,就涉及到了位的扩展,此时由两个字节扩充为四个字节。
在进行位的扩展时,最容易想到的就是在高位全部补0,也就是将原来的二进制序列前面加入若干个0,也称为零扩展。还有一种方式比较特别,是符号扩展,也就是针对有符号数的方式,它是直接扩展符号位,也就是将二进制序列的前面加入若干个最高位。
对于零扩展来说,很明显扩展之后的值与原来的值是相等的,而对于符号扩展来说,则是一样,只不过没有零扩展来的直观。我们在计算补码时有一个比较简单的办法,就是符号位若为0,则与无符号是类似的。若符号位为1,也就是负数时,可以将其余位取反最终再加1即可。因此当我们对一个有符号的负数进行符号扩展时,前面加入若干个1,在取反之后都为0,因此依旧会保持原有的数值。
总之,在对位进行扩展时,是不会改变原有数值的。
在书中对于负数的符号扩展还给出了这一过程的证明,LZ这里就不多做叙述了,其实这个证明很简单,就是利用了补码编码的公式而已。需要多提一句的是,这里使用了归纳法证明,因此这里只是扩展了一位,具体过程如下。
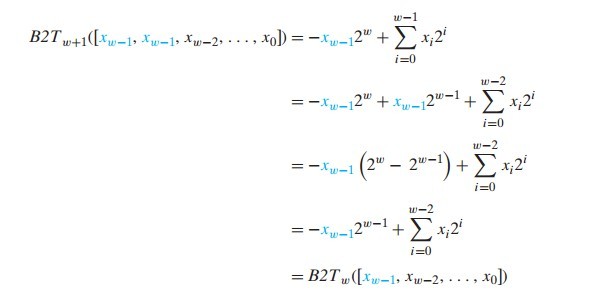
截断
截断与扩展相反,它是将一个多位二进制序列截断至较少的位数,也就是与扩展是相反的过程。
根据我们的直观判断也不难发现,截断可能会导致数据的失真。对于无符号编码来说,截断后就是剩余位数的无符号编码数值。在书中给出了这一简单过程的证明,它主要是想表明截断前与截断后的数值的关系是取模所得到的。

对于补码编码来说,截断后的二进制序列与无符号编码是一样的,因此我们只需要多加一步,将无符号编码转换为补码编码就可以了。
因此对于无符号编码和补码来说,可以得到以下两个公式。
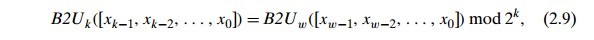
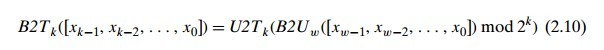
其它语言中的有符号与无符号
从上面的分析不难看出,具有有符号和无符号数的语言,可能会因此引起一些不必要的麻烦,而且无符号数除了能表示的最大值更大以外,似乎并没有太大的好处。因此有很多语言是不支持无符号数的。
比如LZ所使用的Java语言,就只有有符号数,这样省去了很多不必要的麻烦。无符号数很多时候只是为了表示一些无数值意义的标识,比如我们的内存地址,此时的无符号数就有点类似于数据库主键或者说键值对中的键值的概念,仅仅是一个标识而已。
文章小结
本文主要阐述了C语言当中的有符号数和无符号数,以及低位转高位的扩展、高位转低位的截断运算,下一章我们将讲解很重要的一节内容,整数的二进制运算。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号