ZKW线段树学习记录 (1)
zkw线段树讲稿:统计的力量
1、区间求和
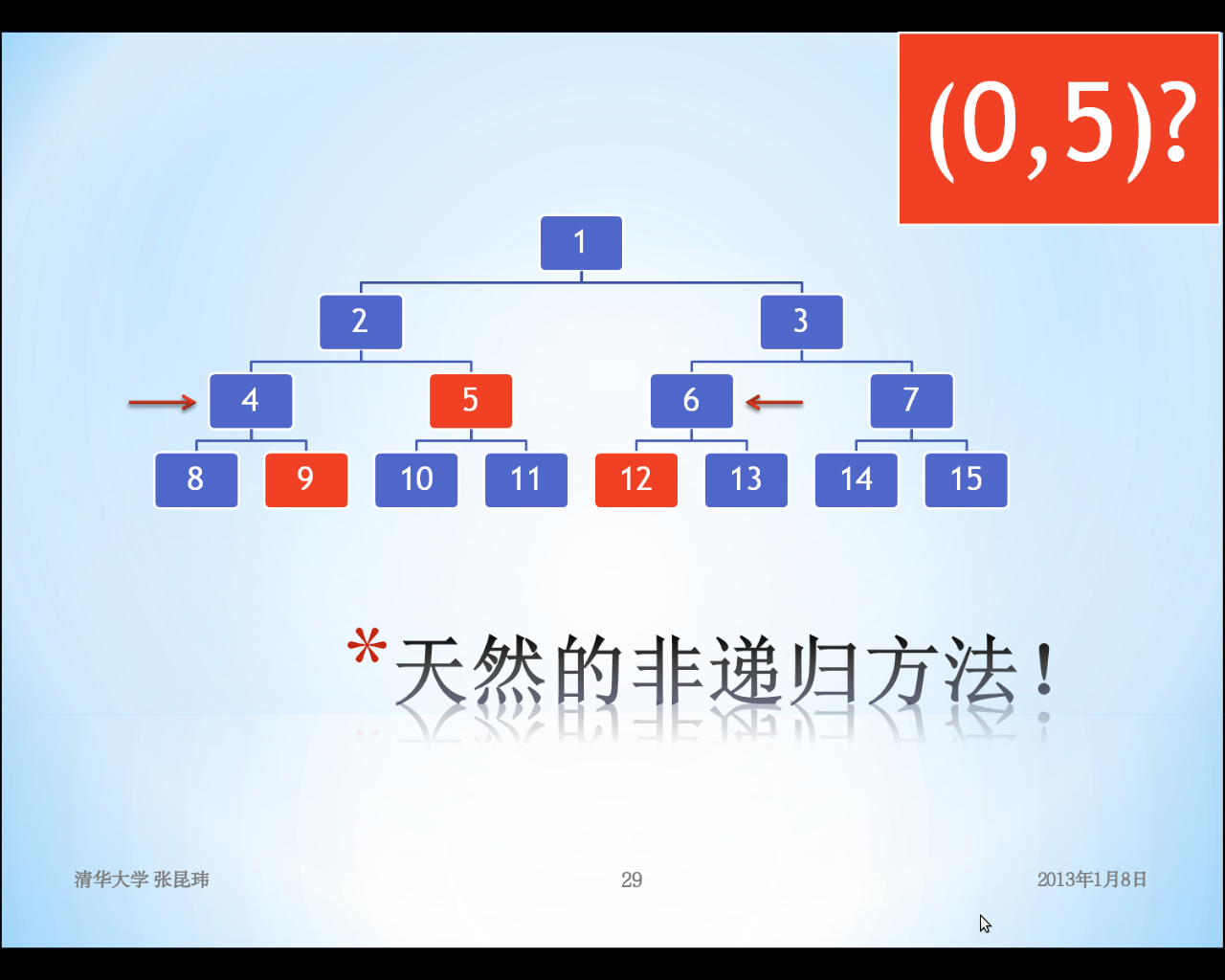
其实zkw线段树的核心思想就是:用1表示根节点,那么每一个节点的值就表示以该节点编号为后缀的所有节点的和。
4=100,其恰好包括了1000=8,1001=9的值。而在X<>2^n-1时,X+1即是其兄弟右节点,X<>2^n时,X-1即是其兄弟左节点。
找第I个叶子节点(0<=i<n):
记录线段树有k层,则叶子节点编号为2^(n-1)+t O(1)
区间和:
Warning:理论上能放 [0,2^N) 的树 其实只能查询 [1,2^N - 2] 的范围
先找到s=s-1,t=t+1的叶子节点,然后不断向上移,若s是左子树,则其右兄弟必在区间内,若t是右子树,左子树必在区间内。然后同时s、t上移一层,直至s、t为相邻的兄弟节点(s xor t=1)
Func Query(s,t) // 询问从s到t闭区间 s = s – 1, t = t + 1; // 变为开区间 s += M, t += M; // 找到叶子位置 M=2^(层数-1) While not ((s xor t) == 1) do //若s与t不相邻 If ((s and 1) == 0) Answer += Tree[s + 1]; //若s是左子树,加上右兄弟 If ((t and 1) == 1) Answer += Tree[t – 1]; //若t是右子树,加上左兄弟 s = s >> 1, t = t >> 1; //上移一层
因为区间和头尾无法求,所以一般多建一层会保险一点,题目中要[0,1023],直接建一个[0,2047]的树就行了。
2、修改
基本和线段树相同,只不过可以直接找到叶子节点。
Func Change(n,NewValue) n += M; //找到叶子节点编号 Tree[n] = NewValue; While n > 1 do n = n >> 1; Tree[n] = Tree[2n] + Tree[2n+1];//递归赋值







