分享读C Primer Plus时遇到的一个问题（补档5月7日）

最近在学习C Primer Plus。书中第66页，3.8 关键概念 这一小节中有这一段话：

 

“计算机中的浮点数和整数在本质上不同，其存储方式和运算过程有很大区别。即使两个 32 位存储单元存储的位组合完全相同，但是一个解释为 float 类型，另一个解释为 long 类型，这两个相同的位组合表示的值也完全不同。例如，在 PC 中，假设一个位组合表示 float 类型的数 256.0，如果将其解释为 long 类型，得到的值是 113246208。C 语言允许编写混合数据类型的表达式，但是会进行自动类型转换，以便在实际运算时统一使用一种类型。“

 

我自己的理解是：有两个长度为32位的存储空间有同样的位组合，它们分别存储了 float 和 long 两种类型。但因为 float 和 long 在计算机中的存储方法和形式不同，导致了输出的值不同。

抛出问题：在验算中我得出的 long 类型的结果为 1132462080，和原文结果不同，较书上数字多了一位 0。

 

首先探讨 float 数据类型的存储形式。

浮点型变量在计算机内存中占用4个字节（4 Byte），即32-bit。这 32 位的存储空间为SEEE EEEE EMMM MMMM MMMM MMMM MMMM MMMM 的格式。

S部分：数符。表示浮点数的正负，1为负数，0为正数。

E部分：阶码。指数加上127后的值的二进制数。

M部分：尾数。规格化表示后底数去除整数位1的二进制数。

Single precision单精度浮点数和 float 浮点数存储形式相同

 

 

*规格化的步骤：

（1）将 float 转化为二进制形式。

（2）用科学计数法表示第一步得到的二进制数，得到的指数加127既是E部分的阶码。

（3）科学计数法的小数部分，即M部分的尾数。

 

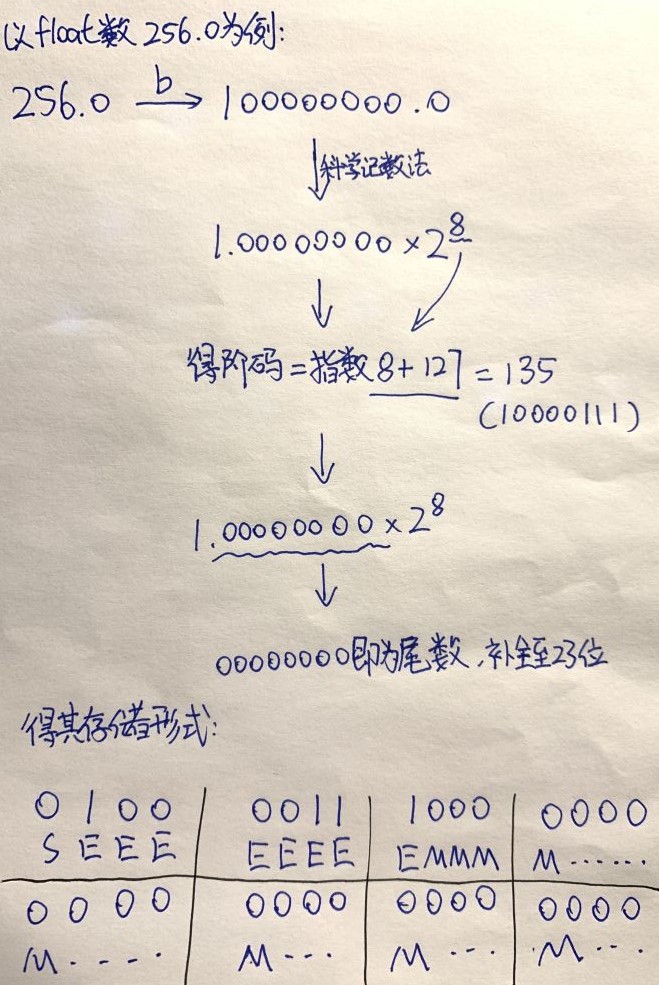
最后可以得到浮点数256.0的存储形式：

0100(SEEE)      0011(EEEE)       1000(EMMM)      0000(MMMM) 

0000(MMMM)   0000(MMMM)     0000(MMMM)     0000(MMMM)

32位的存储空间里包含了1个S，代表正负；8个E为指数。实质上就是这个浮点数其数值的数量级；23个M，即这个数本身由哪些数字组成。

实质上这个32位存储空间就是科学记数法的二进制”变种“，它包含了正负、数字和数量级，即表示了一个数。

 

#两点补充：（1）为什么要给指数加127才是阶码？答：浮点数的指数可正可负，指数E的存储空间是带符号的8位。所以根据IEEE标准，float 的指数取值范围为 -126 到 128，需要加上127来取消负数情况。（2）为什么尾数是规格化后底数去掉整数位 1 的二进制数？答：科学记数法后底数部分实际是占用24bit 的一个值，但是最高位始终为1。所以最高位省去不存储，在存储中占23bit。

 

 

关于 long 长整型数的存储格式，我并没有查到太多的相关资料，大多都是与 int、long long 相关等等。因该就是除了原码、反码、补码相关知识之后，直接首位表正负，其他二进制码就是它的数值。

 

所以把浮点数 256.0 的 32 位存储形式0100 0011 1000 0000 0000 0000 0000 0000转化为 long 得到 1132462080，而非书上的 113246208 。

 

这篇文章的本意是借此机会，来记录一下学习了数据类型存储形式和方法的知识成果。如果能有大神解决了我的问题，那更是再好不过！附上一条帮助我很多的博客的链接：https://www.cnblogs.com/chris-cp/p/4321793.html#undefined