同余最短路学习笔记
C110U01 笔记 同余最短路
目录
KK3233.sums
Description
已知有 3 个正整数,\(a,b,c\) ,希望用他们凑出某个总和,每个数字都可以使用任意次数。给定正整数 \(t\) ,请问从 1 到 \(t\) 里,共有多少个数字可以恰好凑出来?
输入文件 sums.in
第一行为正整数 \(t,a,b,c\)
输出文件 sums.out
输出一行,包含一个整数
对于 100% 的数据,保证 \(t \le 2^{63}-1 \, , 1 \le a,b,c \le 100000\)
Solution
模型分析:背包模型 —— 凑和模型
难点:背包容量太$ \color{red}大$
难点:凑\(\color{red}大\)数
启发思路
可行性问题:01 序列
超过一定数值后全部都可以凑到
同余最短路
在模世界中建图
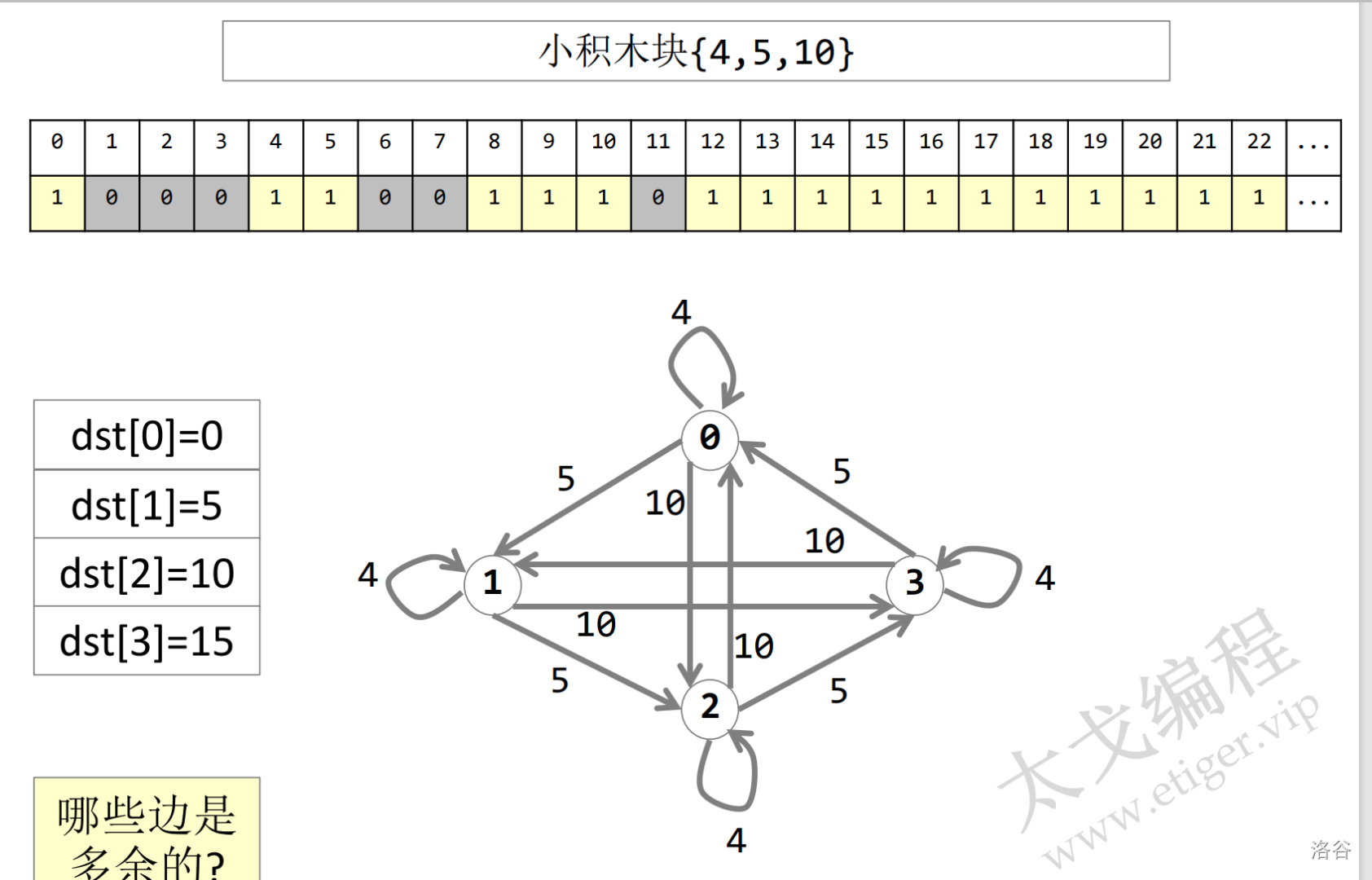
模数选取:选众多小积木块中的最小数值 MOD
每个节点对应一个同余系
每条边对应使用了一个小积木块,边权为该数值大小
求解 dst[r] 表示模 MOD 余 r 的数字中,最小的能凑出的数字是几
e.g.

e.g.
Code
注意:隐式图
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=10;
const ll V=1e5+10;
const ll INF=(1LL<<62)-1+(1LL<<62); //防溢出
ll nV;
ll nDgr=3;
ll val[N];
ll dst[V];
bool ok[V];
struct Node{
ll u,c;
bool operator<(const Node&x)const{
return c>x.c;
}
}
void Dijkstra(){
priority_queue<Node> q;
fill(dst,dst+nV+1,INF);
fill(ok,ok+nV+1,0);
dst[0]=0;
q.push((Node){0,0});
while(!q.empty()){
Node now=q.top(); q.pop();
ll u=now.u;
if(ok[u])continue;
ok[u]=1;
for(ll i=1;i<=nDgr;i++){
ll v=(u+val[i])%nV;
if(ok[v])continue;
ll cost=dst[u]+val[i];
if(dst[v]<=cost)continue;
dst[v]=cost;
q.push((Node){v,dst[v]});
}
}
}
ll query(ll x){
ll ret=0;
for(int i=0;i<nV;i++)
if(dst[i]<=x)
res+=(x-dst[i])/nV+1;
//易错点:0 也被统计到
return ret;
}
int main(){
ll t;
scanf("%lld",&t);
for(ll i=1;i<=nDgr;i++)
scanf("%lld",&val[i]);
nV=*min_element(val+1,val+1+nDgr);
Dijkstra();
printf("%lld\n",query(t)-1);
//query(x) 表示在 0 到 t 中可以凑出几个数
}
易错点:
- 模世界的图里节点数不是原题中的 n
- nDgr 和 nV 容易混淆
核心算法思想总结
- 识别出 01 问题的答案分布
- 可行性问题转换为最优化问题
- 在众多同类型的可行解里,识别出最具代表性的一个可行解
KK3234.bags (Luogu P2371)
Description
已知有 \(n\) 种物品,每种物品都有无限多件,第 \(i\)种物品每件体积为 \(v[i]\) 。现在有多个问询,形式为:能否恰好装满容积为 \(c\) 的背包?这里的 \(c\) 有取值范围:\([a,b]\) 之间的正整数,每个数字对应一个问询,共有 \(b-a+1\) 个问询。请问共有多少个问询的答案为“能”?
输入文件 bags.in 第一行为正整数 \(n,a,b\) 。接下来一行包含 \(n\)个整数,代表\(v[i]\)。
输出文件 bags.out 输出一行,包含一个整数。
对于100%的数据,\(n \le 12,0 \le v[i] \le 500000,1 \le a \le b \le 1000000000000\)。
Solution
易错点:特判 \(v[i]\) 为 0 的情况
int main(){
ll a,b;
scanf("%lld %lld %lld",&nDgr,&a,&b);
for(ll i=1;i<=nDgr;i++){
scanf("%lld",&val[i]);
if(val[i])continue;
i--;
nDgr--;
}
nV=*min_element(val+1,val+1+nDgr);
Dijkstra();
ll ans=query(b)-query(a-1);
printf("%lld\n",ans);
}
KK3235.length
Desciption
有 \(N\) 种木棍每种足够多,长度为 \(L_1,L_2,\dots,L_N\) , 希望找到 一个最大的不能够被凑出的长度。在凑长度时,每一根使用的木棍最多可以被削短 \(M\) 米。
输出最大的不能被凑出的长度,如果不存在,输出 -1 .
输入文件 length.in
第一行包含两个整数 \(N,M\)
下面 \(N\) 行,每行一个整数 \(L_i\)
输出文件 length.out
输出一行,答案或者 -1
对于 50% 的数据,保证 \(1 \le N \le 10 , 1 \le M \le 30\)
对于 100% 的数据,保证 \(1 \le N \le 100 , 1 \le M \le 300 , 1 < L_i < 3000\)
Solution
dst[r] 表示模 MOD 余 r 的数字中,最小的能凑出的数字是几
所以模 MOD 余 r 的数字中,最大的不能凑出的是 dst[r]-MOD
使用 Dijkstra 朴素版
KK3077.collection
Description
有 \(n\) 个完全平方数,他们的和为 \(S\) ,每个完全平方数都在 \([1,50]\) 中 (即是\(\{ 1,4,9,16,25,36,49 \}\) 中的一个)。
求 \(n\) 最小为几
输入文件 collection.in
输入一个正整数 \(S\)
输出文件 collection.out
输出一个正整数表示最小的 \(n\)
输入输出样例 1:
| \(\text{collection.in}\) | \(\text{collection.out}\) |
|---|---|
| 100 | 4 |
输入输出样例 2:
| \(\text{collection.in}\) | \(\text{collection.out}\) |
|---|---|
| 35 | 3 |
Solution
为什么这题不能使用同余最短路
同余最短路是用于处理批量最优解的技术,但是本题只需要对于一个 \(n\) 计算最优解。
拓展题:CF986F Oppa Funcan Style Remastered
Description
多个问询:能否用 \(k\) 的质因子凑出 \(n\)
Solution
\(k\) 的可能性最多只有 50 种,可以预处理分解质因数



