数据结构06——优先队列和堆

开头语

因为这些日子的懒惰，所以一直没有更新博客，实在在很抱歉。这里我将继续和大家分享数据结构的知识，希望大家可以喜欢。本篇文章我将会分享关于优先队列和堆的相关知识，那么我们来说下，关于这两种数据结构的各自相关的文字定义。

首先，先说下什么是优先队列，其实在前面数据结构02——栈和队列这篇文章中，我们已经介绍过了关于队列的知识，之前说过队列就像我们日常生活中的排队，先进的先出，但是对于优先队列，它却并不遵守这样的规则，优先队列表现的更像是我们去医院急诊看病一样，医生会根据病人病情的轻重来安排谁先看。对于优先队列是一种抽象数据类型，它表示了一组值和对这组值的操作，后面我们将会用代码来体现。

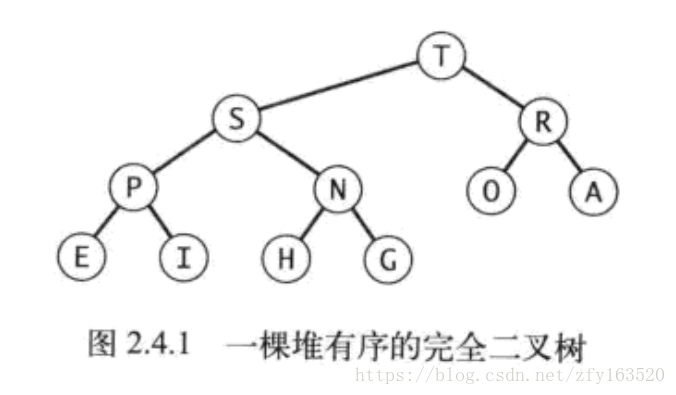
接下来继续说一下什么是堆，其实堆它也是一棵树，所以我们会经常看到什么二叉堆、多叉堆这样的一些名词。长话短说，我们还是来说下堆的具体定义，当一棵二叉树的每个节点都大于等于它的两个子节点，他被称为堆有序。而对于二叉堆而言，它是能够很好的体现优先队列的基本操作的，图中就是堆的表示方式。

图1：堆的表示

一.堆的定义及实现

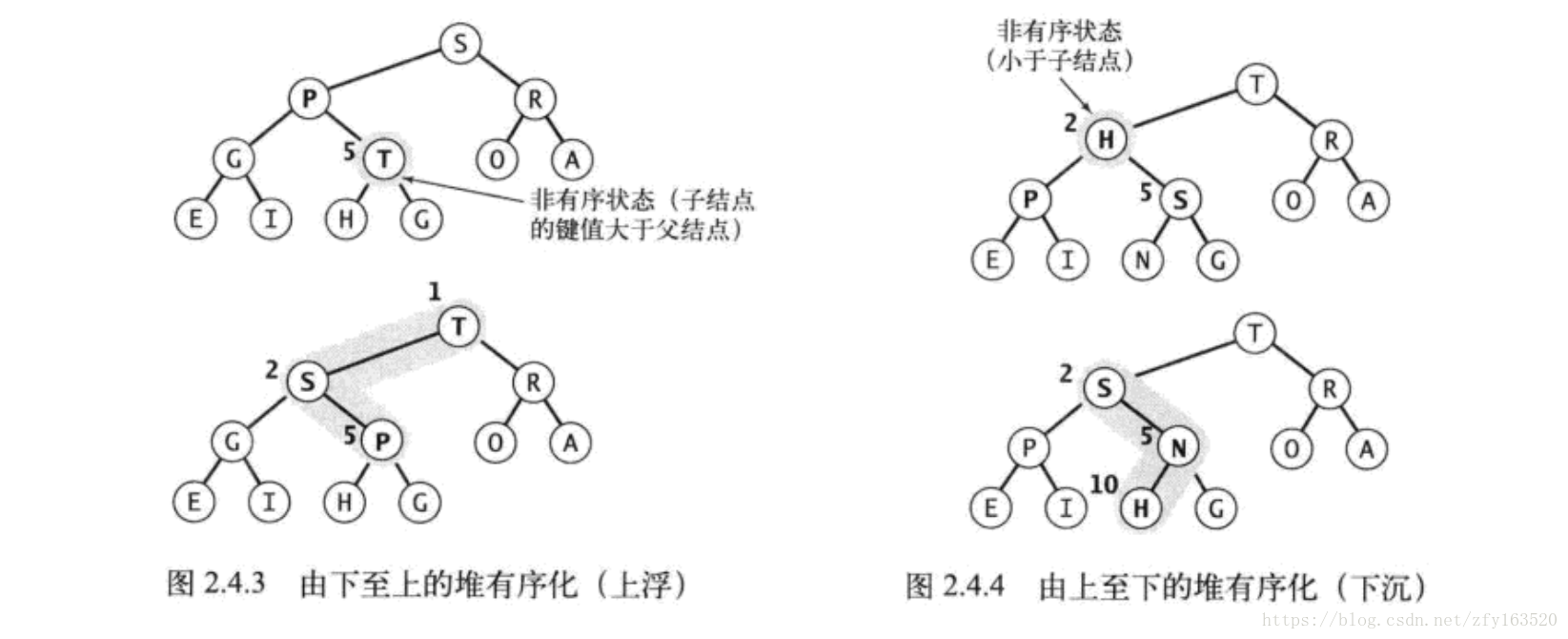
这里的堆是基于数组来实现的，所以这里对于数组的代码我就不贴出来了，大家可以去前面的文章中看看。在这个节段中，我们的代码主要实现了向堆中添加、删除、搜索等等相关功能。因为是以最大堆来体现的，因此里面还实现了siftUp和siftDown的相关操作。对于siftUp而言，，就是在堆中，它的有序状态因为某个节点变得比它的父节点更大而被打破，那么我们就需要通过交换它和它的父节点来修复这样的一个不平衡的状态。而对于siftDown而言，就是因为堆的有序状态因为某个节点而变得比它的两个子节点或是其中之一更小而打破了，那么我们就要来交换他们的位置来修复这样的不平衡状态。

图2：堆的上浮和下沉

 

package com.zfy.headandqueue;

public class MaxHeap<E extends Comparable<E>> {

    private Array<E> data;
    
    public MaxHeap(int capacity) {
        data = new Array<>();
    }
    
    public MaxHeap(){
        data = new Array<>();
    }
    
    // Heapify的实现（将任意数组整理成树结构） 
    public MaxHeap(E[] arr){
        data = new Array<>(arr);
        for (int i = parent(arr.length - 1); i >= 0; i--) {
            siftDown(i);
        }
    }
    
    //返回堆中的元素个数
    public int size() {
        return data.getSize();
    }
    
    //返回一个布尔值，表示堆是否为空
    public boolean isEmpty() {
        return data.isEmpty();
    }
    
    //返回完全二叉树的数组表示中，一个索引所表示的元素的父节点的索引
    public int parent(int index) {
        if (index == 0) 
            throw new IllegalArgumentException("index-0 doesn't have parent." );
        return (index-1)/2;
    }
    
    //返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    public int leftChild(int index) {
        return index * 2 +1;
    }
    
    //返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    public int rightChild(int index) {
        return index * 2 + 2;
    }
    
    //向堆中添加元素
    public void add(E e) {
        data.addLast(e);
        siftUp(data.getSize() - 1);
    }

    //上浮操作
    private void siftUp(int k) {
        
        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
            data.swap(k, parent(k));
            k = parent(k);
        }
        
    }
    
    //看堆中最大元素
    public E findMax() {
        if (data.getSize() == 0) {
            throw new IllegalArgumentException("Can not findMax when heap is empty.");
        }
        return data.get(0);
    }
    
    //取出堆中最大元素
    public E extractMax() {
        E ret = findMax();
        data.swap(0, data.getSize() - 1);//交换数组0位置的元素和数组最后位置的元素
        data.removeLast();//移除最后一个元素
        siftDown(0);
        return ret;
    }

    //下沉操作
    private void siftDown(int k) {
        
        while (leftChild(k) < data.getSize()) {
            int j = leftChild(k);// 在此轮循环中,data[k]和data[j]交换位置
            if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
                j ++;
//                j = rightChild(k);
                // data[j] 是 leftChild 和 rightChild 中的最大值
            }
            if (data.get(k).compareTo(data.get(j)) >= 0) {
                break;
            }
            data.swap(k, j);
            k = j;
        }
        
    }
    
    //取出堆中的最大元素， 并且替换成e元素
    public E replace(E e) {
        E ret = findMax();
        data.set(0, e);
        siftDown(0);
        return ret;
    }
}
 

 

二.优先队列的定义及实现

 

1.优先队列接口的定义

package com.zfy.headandqueue;

public interface Queue<E> {

    int getSize();//获取队列size
    boolean isEmpty();//判断队列是否为空
    void enqueue(E e);//入队操作
    E dequeue();//出队操作
    E getFront();//获取 front
}

 

2.优先队列的实现

package com.zfy.headandqueue;

public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

    private MaxHeap<E> maxHeap;

    public PriorityQueue(){
        maxHeap = new MaxHeap<>();
    }

    @Override
    public int getSize(){
        return maxHeap.size();
    }

    @Override
    public boolean isEmpty(){
        return maxHeap.isEmpty();
    }

    @Override
    public E getFront(){
        return maxHeap.findMax();
    }

    @Override
    public void enqueue(E e){
        maxHeap.add(e);
    }

    @Override
    public E dequeue(){
        return maxHeap.extractMax();
    }
}

 

 

结束语：温故而知新，可以为师矣！

参考：bobobo老师的玩转数据结构和算法4

版权声明：尊重博主原创文章，转载请注明出处 https://www.cnblogs.com/hsdy