数据结构09—— 并查集（Union-Find）

一、关于并查集

并查集（Union-Find）是一种树型的数据结构，常用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。并查集（Union-Find）从名字可以看出，主要它涉及两种基本操作:合并和查找。这说明，初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成一个大的集合。

 

二、并查集的设计和基本实现

 

1.并查集接口的设计

public interface UF {
    
    int getSize();
    boolean isConnected(int p, int q);
    void unionElements(int p, int q);
    
}
 

 

2.第一版本的并查集实现：基于数组

package com.zfy.uf;

public class UnionFind1 implements UF {

    private int[] id; // 我们的第一版Union-Find本质就是一个数组

    public UnionFind1(int size) {

        id = new int[size];
        // 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < id.length; i++) {
            id[i] = i;
        }

    }

    @Override
    public int getSize() {
        return id.length;
    }

    // 查找元素p所对应的集合编号
    // O(1)复杂度
    private int find(int p) {
        if (p < 0 || p >= id.length)
            throw new IllegalArgumentException("p is out of bound.");
        return id[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(1)复杂度
    @Override
    public boolean isConnected(int p, int q) {

        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(n) 复杂度
    @Override
    public void unionElements(int p, int q) {

        int pID = find(p);
        int qID = find(q);

        if (pID == qID) {
            return;
        }

        for (int i = 0; i < id.length; i++) {
            // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
            if (id[i] == pID) {
                id[i] = qID;
            }
        }

    }

}
 

 

3.第二版的并查集

package com.zfy.uf;

public class UnionFind2 implements UF {

    // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;

    // 构造函数
    public UnionFind2(int size) {

        parent = new int[size];

        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for (int i = 0; i < size; i++)
            parent[i] = i;
    }

    @Override
    public int getSize() {
        return parent.length;
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p) {

        if (p < 0 || p >= parent.length)
            throw new IllegalArgumentException("p is out of bound.");

        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while (p != parent[p])
            p = parent[p];
        return p;

    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    @Override
    public void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot)
            return;

        parent[pRoot] = qRoot;
    }

}
 

 

4. 基于size的优化

package com.zfy.arithmetic.unionfnd;

/**
 * Created by vincent on 2018/10/15 上午10:13
 */
public class UnionFind3 implements UF {

    private int[] parent; // parent[i]表示第一个元素所指向的父节点
    private int[] sz;     // sz[i]表示以i为根的集合中元素个数

    // 构造函数
    public UnionFind3(int size){

        parent = new int[size];
        sz = new int[size];

        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for(int i = 0 ; i < size ; i ++){
            parent[i] = i;
            sz[i] = 1;
        }
    }

    @Override
    public int getSize(){
        return parent.length;
    }
    
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        if(p < 0 || p >= parent.length)
            throw new IllegalArgumentException("p is out of bound.");

        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    @Override
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    @Override
    public void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if(pRoot == qRoot)
            return;

        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if(sz[pRoot] < sz[qRoot]){
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }
        else{ // sz[qRoot] <= sz[pRoot]
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}

 

5.Main测试方法

 

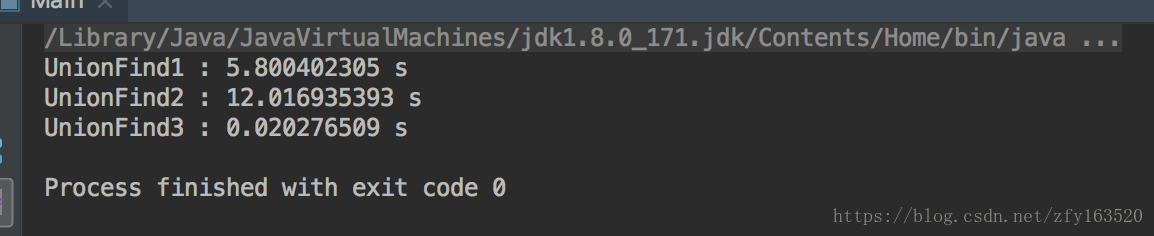
package com.zfy.arithmetic.unionfnd;

import java.util.Random;

public class Main {

    private static double testUF(UF uf, int m){

        int size = uf.getSize();
        Random random = new Random();

        long startTime = System.nanoTime();


        for(int i = 0 ; i < m ; i ++){
            int a = random.nextInt(size);
            int b = random.nextInt(size);
            uf.unionElements(a, b);
        }

        for(int i = 0 ; i < m ; i ++){
            int a = random.nextInt(size);
            int b = random.nextInt(size);
            uf.isConnected(a, b);
        }

        long endTime = System.nanoTime();

        return (endTime - startTime) / 1000000000.0;
    }

    public static void main(String[] args) {

        // UnionFind1 慢于 UnionFind2
//        int size = 100000;
//        int m = 10000;

        // UnionFind2 慢于 UnionFind1, 但UnionFind3最快
        int size = 100000;
        int m = 100000;

        UnionFind1 uf1 = new UnionFind1(size);
        System.out.println("UnionFind1 : " + testUF(uf1, m) + " s");

        UnionFind2 uf2 = new UnionFind2(size);
        System.out.println("UnionFind2 : " + testUF(uf2, m) + " s");

        UnionFind3 uf3 = new UnionFind3(size);
        System.out.println("UnionFind3 : " + testUF(uf3, m) + " s");
    }
}
 

 

测试结果:

 

因为本人太懒,一直没有画图,以后一定会改进!!!!!

结束语：合抱之木，生于毫末；九层之台，起于累土；千里之行，始于足下。

参考：bobobo老师的玩转数据结构

版权声明：尊重博主原创文章，转载请注明出处 https://www.cnblogs.com/hsdy