Codeforces Round #310 (Div. 2) A B C

Andrewid the Android is a galaxy-famous detective. In his free time he likes to think about strings containing zeros and ones.

Once he thought about a string of length n consisting of zeroes and ones. Consider the following operation: we choose any two adjacent positions in the string, and if one them contains 0, and the other contains 1, then we are allowed to remove these two digits from the string, obtaining a string of length n - 2 as a result.

Now Andreid thinks about what is the minimum length of the string that can remain after applying the described operation several times (possibly, zero)? Help him to calculate this number.

Input

First line of the input contains a single integer n (1 ≤ n ≤ 2·10⁵), the length of the string that Andreid has.

The second line contains the string of length n consisting only from zeros and ones.

Output

Output the minimum length of the string that may remain after applying the described operations several times.

Examples

Input

4
1100

Output

Input

5
01010

Output

Input

8
11101111

Output

Note

In the first sample test it is possible to change the string like the following: 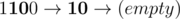$\text{[math]}$ .

In the second sample test it is possible to change the string like the following: 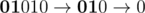$\text{[math]}$ .

In the third sample test it is possible to change the string like the following: $\text{[math]}$ .

题意：

题解：

 1 /******************************
 2 code by drizzle
 3 blog: www.cnblogs.com/hsd-/
 4 ^ ^    ^ ^
 5  O      O
 6 ******************************/
 7 #include<bits/stdc++.h>
 8 #include<map>
 9 #include<set>
10 #include<cmath>
11 #include<queue>
12 #include<bitset>
13 #include<math.h>
14 #include<vector>
15 #include<string>
16 #include<stdio.h>
17 #include<cstring>
18 #include<iostream>
19 #include<algorithm>
20 #pragma comment(linker, "/STACK:102400000,102400000")
21 using namespace std;
22 #define  A first
23 #define B second
24 const int N=50010;
25 const int mod=1000000007;
26 const int MOD1=1000000007;
27 const int MOD2=1000000009;
28 const double EPS=0.00000001;
29 //typedef long long ll;
30 typedef __int64 ll;
31 const ll MOD=1000000007;
32 const int INF=1000000010;
33 const ll MAX=1ll<<55;
34 const double eps=1e-5;
35 const double inf=~0u>>1;
36 const double pi=acos(-1.0);
37 typedef double db;
38 typedef unsigned int uint;
39 typedef unsigned long long ull;
40 int n;
41 char  a[200005];
42 int main()
43 {
44     scanf("%d",&n);
45     scanf("%s",a+1);
46     int jishu1=0;
47     int jishu2=0;
48     for(int i=1;i<=n;i++)
49     {
50         if(a[i]=='0')
51             jishu1++;
52         else
53             jishu2++;
54     }
55     cout<<n-2*min(jishu1,jishu2)<<endl;
56     return 0;
57 }

Andrewid the Android is a galaxy-famous detective. He is now investigating a case of frauds who make fake copies of the famous Stolp's gears, puzzles that are as famous as the Rubik's cube once was.

Its most important components are a button and a line of n similar gears. Each gear has n teeth containing all numbers from 0 to n - 1 in the counter-clockwise order. When you push a button, the first gear rotates clockwise, then the second gear rotates counter-clockwise, the the third gear rotates clockwise an so on.

Besides, each gear has exactly one active tooth. When a gear turns, a new active tooth is the one following after the current active tooth according to the direction of the rotation. For example, if n = 5, and the active tooth is the one containing number 0, then clockwise rotation makes the tooth with number 1 active, or the counter-clockwise rotating makes the tooth number 4 active.

Andrewid remembers that the real puzzle has the following property: you can push the button multiple times in such a way that in the end the numbers on the active teeth of the gears from first to last form sequence 0, 1, 2, ..., n - 1. Write a program that determines whether the given puzzle is real or fake.

Input

The first line contains integer n (1 ≤ n ≤ 1000) — the number of gears.

The second line contains n digits a₁, a₂, ..., a_n (0 ≤ a_i ≤ n - 1) — the sequence of active teeth: the active tooth of the i-th gear contains number a_i.

Output

In a single line print "Yes" (without the quotes), if the given Stolp's gears puzzle is real, and "No" (without the quotes) otherwise.

Examples

Input

3
1 0 0

Output

Yes

Input

5
4 2 1 4 3

Output

Yes

Input

4
0 2 3 1

Output

No

Note

In the first sample test when you push the button for the first time, the sequence of active teeth will be 2 2 1, when you push it for the second time, you get 0 1 2.

 1 /******************************
 2 code by drizzle
 3 blog: www.cnblogs.com/hsd-/
 4 ^ ^    ^ ^
 5  O      O
 6 ******************************/
 7 #include<bits/stdc++.h>
 8 #include<map>
 9 #include<set>
10 #include<cmath>
11 #include<queue>
12 #include<bitset>
13 #include<math.h>
14 #include<vector>
15 #include<string>
16 #include<stdio.h>
17 #include<cstring>
18 #include<iostream>
19 #include<algorithm>
20 #pragma comment(linker, "/STACK:102400000,102400000")
21 using namespace std;
22 #define  A first
23 #define B second
24 const int N=50010;
25 const int mod=1000000007;
26 const int MOD1=1000000007;
27 const int MOD2=1000000009;
28 const double EPS=0.00000001;
29 //typedef long long ll;
30 typedef __int64 ll;
31 const ll MOD=1000000007;
32 const int INF=1000000010;
33 const ll MAX=1ll<<55;
34 const double eps=1e-5;
35 const double inf=~0u>>1;
36 const double pi=acos(-1.0);
37 typedef double db;
38 typedef unsigned int uint;
39 typedef unsigned long long ull;
40 int n;
41 int a[1005];
42 int b[1005];
43 int main()
44 {
45     scanf("%d",&n);
46     for(int i=1;i<=n;i++)
47         scanf("%d",&a[i]);
48     for(int i=1;i<=n;i++)
49     {
50         if(i%2)
51             b[i]=(i-1-a[i]+n)%n;
52         else
53             b[i]=(a[i]-(i-1)+n)%n;
54     }
55     for(int i=1;i<n;i++)
56     {
57         if(b[i]!=b[i+1])
58         {
59             cout<<"No"<<endl;
60             return 0;
61         }
62     }
63     cout<<"Yes"<<endl;
64     return 0;
65 }

Andrewid the Android is a galaxy-famous detective. He is now investigating the case of vandalism at the exhibition of contemporary art.

The main exhibit is a construction of n matryoshka dolls that can be nested one into another. The matryoshka dolls are numbered from 1 to n. A matryoshka with a smaller number can be nested in a matryoshka with a higher number, two matryoshkas can not be directly nested in the same doll, but there may be chain nestings, for example, 1 → 2 → 4 → 5.

In one second, you can perform one of the two following operations:

Having a matryoshka a that isn't nested in any other matryoshka and a matryoshka b, such that b doesn't contain any other matryoshka and is not nested in any other matryoshka, you may put a in b;
Having a matryoshka a directly contained in matryoshka b, such that b is not nested in any other matryoshka, you may get a out of b.

According to the modern aesthetic norms the matryoshka dolls on display were assembled in a specific configuration, i.e. as several separate chains of nested matryoshkas, but the criminal, following the mysterious plan, took out all the dolls and assembled them into a single large chain (1 → 2 → ... → n). In order to continue the investigation Andrewid needs to know in what minimum time it is possible to perform this action.

Input

The first line contains integers n (1 ≤ n ≤ 10⁵) and k (1 ≤ k ≤ 10⁵) — the number of matryoshkas and matryoshka chains in the initial configuration.

The next k lines contain the descriptions of the chains: the i-th line first contains number m_i (1 ≤ m_i ≤ n), and then m_i numbers a_i1, a_i2, ..., a_{im_i} — the numbers of matryoshkas in the chain (matryoshka a_i1 is nested into matryoshka a_i2, that is nested into matryoshka a_i3, and so on till the matryoshka a_{im_i} that isn't nested into any other matryoshka).

It is guaranteed that m₁ + m₂ + ... + m_k = n, the numbers of matryoshkas in all the chains are distinct, in each chain the numbers of matryoshkas follow in the ascending order.

Output

In the single line print the minimum number of seconds needed to assemble one large chain from the initial configuration.

Examples

Input

3 2
2 1 2
1 3

Output

Input

Output

Note

In the first sample test there are two chains: 1 → 2 and 3. In one second you can nest the first chain into the second one and get 1 → 2 → 3.

In the second sample test you need to disassemble all the three chains into individual matryoshkas in 2 + 1 + 1 = 4 seconds and then assemble one big chain in 6 seconds.

 1 /******************************
 2 code by drizzle
 3 blog: www.cnblogs.com/hsd-/
 4 ^ ^    ^ ^
 5  O      O
 6 ******************************/
 7 #include<bits/stdc++.h>
 8 #include<map>
 9 #include<set>
10 #include<cmath>
11 #include<queue>
12 #include<bitset>
13 #include<math.h>
14 #include<vector>
15 #include<string>
16 #include<stdio.h>
17 #include<cstring>
18 #include<iostream>
19 #include<algorithm>
20 #pragma comment(linker, "/STACK:102400000,102400000")
21 using namespace std;
22 #define  A first
23 #define B second
24 const int mod=1000000007;
25 const int MOD1=1000000007;
26 const int MOD2=1000000009;
27 const double EPS=0.00000001;
28 //typedef long long ll;
29 typedef __int64 ll;
30 const ll MOD=1000000007;
31 const int INF=1000000010;
32 const ll MAX=1ll<<55;
33 const double eps=1e-5;
34 const double inf=~0u>>1;
35 const double pi=acos(-1.0);
36 typedef double db;
37 typedef unsigned int uint;
38 typedef unsigned long long ull;
39 int n,k;
40 int m,exm;
41 vector<int >ve[100005];
42 int main()
43 {
44     scanf("%d %d",&n,&k);
45     for(int i=1;i<=k;i++)
46     {
47         scanf("%d",&exm);
48         for(int j=1;j<=exm;j++)
49         {
50             scanf("%d",&m);
51             ve[i].push_back(m);
52         }
53     }
54     int ans=0;
55     for(int i=1;i<=k;i++)
56     {
57         if(ve[i][0]==1)
58         {
59 
60          for(int j=1;j<ve[i].size();j++)
61          {
62              if(ve[i][j]==ve[i][j-1]+1)
63                 ans++;
64                 else
65             break;
66          }
67         }
68     }
69     cout<<(n-k-ans)+(n-1-ans)<<endl;
70     return 0;
71 }

posted on 2016-10-01 21:56 半根毛线阅读(335) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

Codeforces Round #310 (Div. 2) A B C