B. Bear and Finding Criminals
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

There are n cities in Bearland, numbered 1 through n. Cities are arranged in one long row. The distance between cities i and j is equal to |i - j|.

Limak is a police officer. He lives in a city a. His job is to catch criminals. It's hard because he doesn't know in which cities criminals are. Though, he knows that there is at most one criminal in each city.

Limak is going to use a BCD (Bear Criminal Detector). The BCD will tell Limak how many criminals there are for every distance from a city a. After that, Limak can catch a criminal in each city for which he is sure that there must be a criminal.

You know in which cities criminals are. Count the number of criminals Limak will catch, after he uses the BCD.

Input

The first line of the input contains two integers n and a (1 ≤ a ≤ n ≤ 100) — the number of cities and the index of city where Limak lives.

The second line contains n integers t1, t2, ..., tn (0 ≤ ti ≤ 1). There are ti criminals in the i-th city.

Output

Print the number of criminals Limak will catch.

Examples
Input
6 3
1 1 1 0 1 0
Output
3
Input
5 2
0 0 0 1 0
Output
1
Note

In the first sample, there are six cities and Limak lives in the third one (blue arrow below). Criminals are in cities marked red.

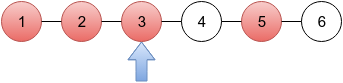
Using the BCD gives Limak the following information:

  • There is one criminal at distance 0 from the third city — Limak is sure that this criminal is exactly in the third city.
  • There is one criminal at distance 1 from the third city — Limak doesn't know if a criminal is in the second or fourth city.
  • There are two criminals at distance 2 from the third city — Limak is sure that there is one criminal in the first city and one in the fifth city.
  • There are zero criminals for every greater distance.

So, Limak will catch criminals in cities 1, 3 and 5, that is 3 criminals in total.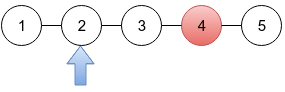

In the second sample (drawing below), the BCD gives Limak the information that there is one criminal at distance 2 from Limak's city. There is only one city at distance 2 so Limak is sure where a criminal is.

 

题意：输入n，a    n个城市，每个城市间的距离为1，警察在第a个城市   每个城市有或没有罪犯用1/0表示  某个仪器能够判断距离警察一定距离的城市里有多少罪犯  当确定某个城市有罪犯时 警察才能抓捕  问警察能抓多少个罪犯

题解： 从警察所在的城市起 若左右等距的城市都有罪犯 则都能抓捕 若只有一个 则无法判断在哪个方向

        两个队列处理 （水）

 

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<algorithm>
 5 #include<queue>
 6 #define ll __int64
 7 using namespace std;
 8 queue<int>q1,q2;
 9 int n,a;
10 int b[105];
11 int main()
12 {
13      int ans=0;
14      scanf("%d %d",&n,&a);
15      for(int i=1;i<=n;i++)
16      scanf("%d",&b[i]);
17      for(int i=a-1;i>=1;i--)
18      q1.push(b[i]);
19      for(int i=a+1;i<=n;i++)
20      q2.push(b[i]);
21      if(b[a])
22      ans++;
23      while(q1.size()>0&&q2.size()>0)
24      {
25          if(q1.front()==1&&q2.front()==1)
26          ans+=2;
27          q1.pop();
28          q2.pop();
29      } 
30      while(q1.size()>0)
31      {
32          if(q1.front()==1)
33          ans++;
34          q1.pop();
35      }
36      while(q2.size()>0)
37      {
38          if(q2.front()==1)
39          ans++;
40          q2.pop();
41      }
42      cout<<ans<<endl;
43     return 0;
44 }