数学基础03-初等函数
初等函数
1 常值函数
常值函数
它的图像时平行于
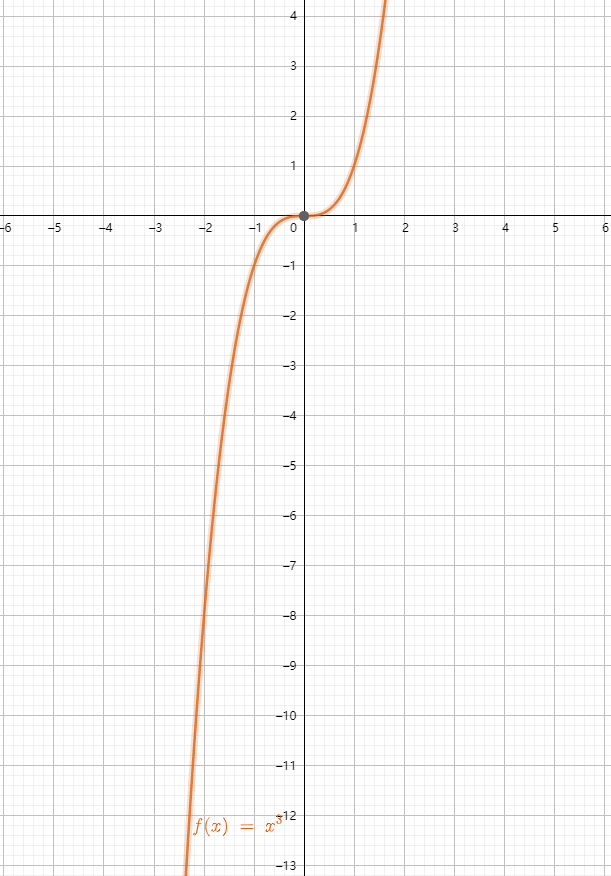
2 幂函数
幂函数
常用的幂函数有以下几个
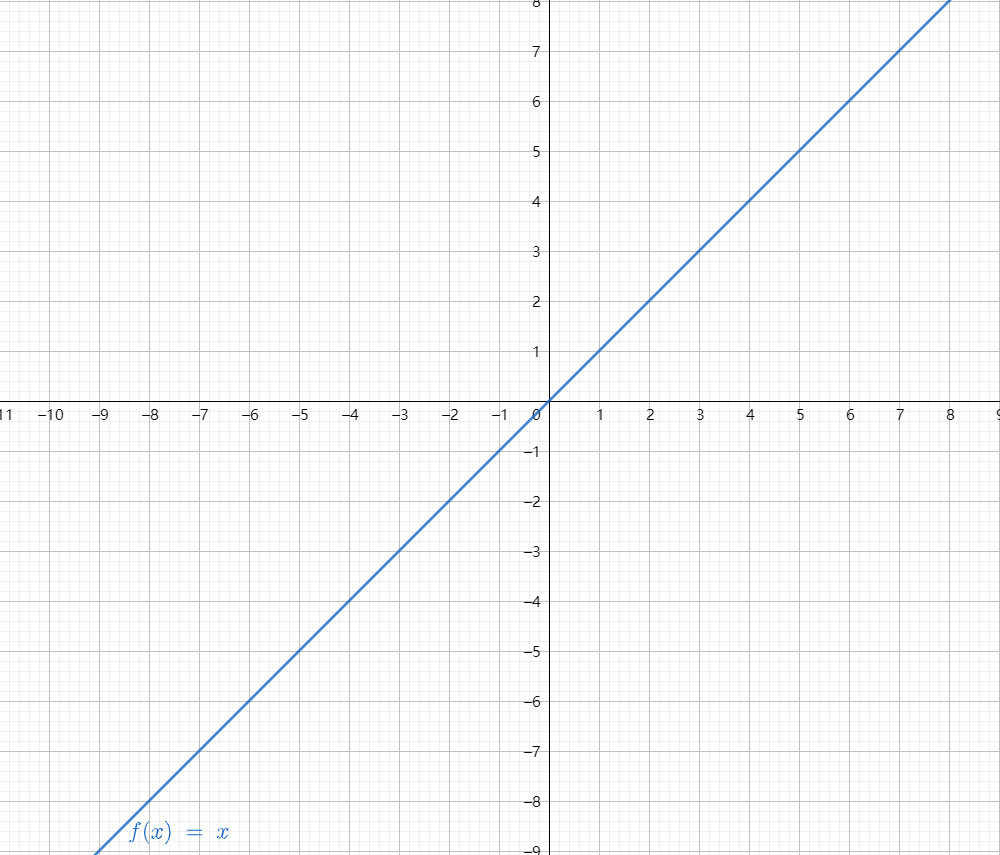
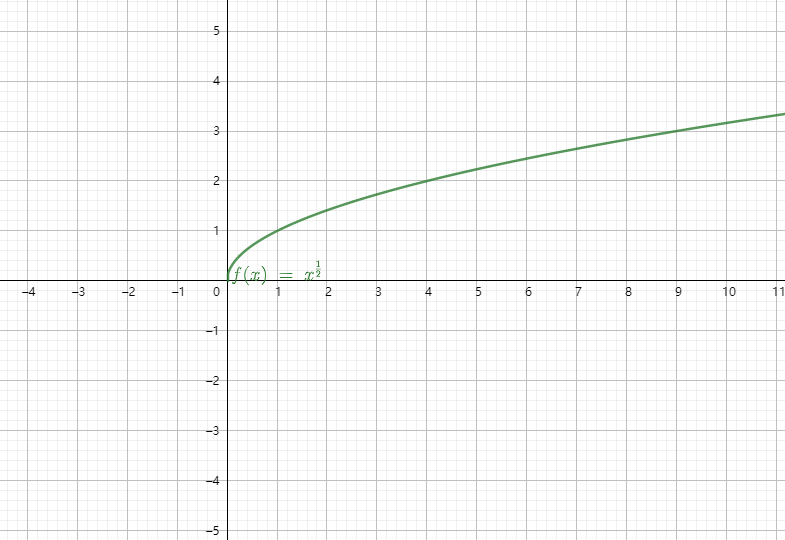
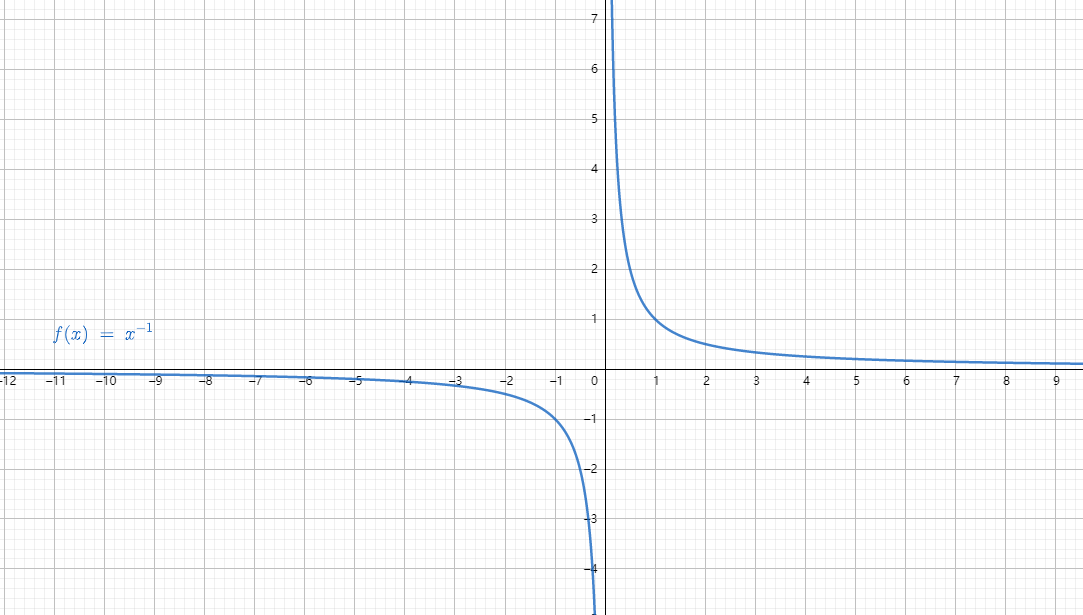
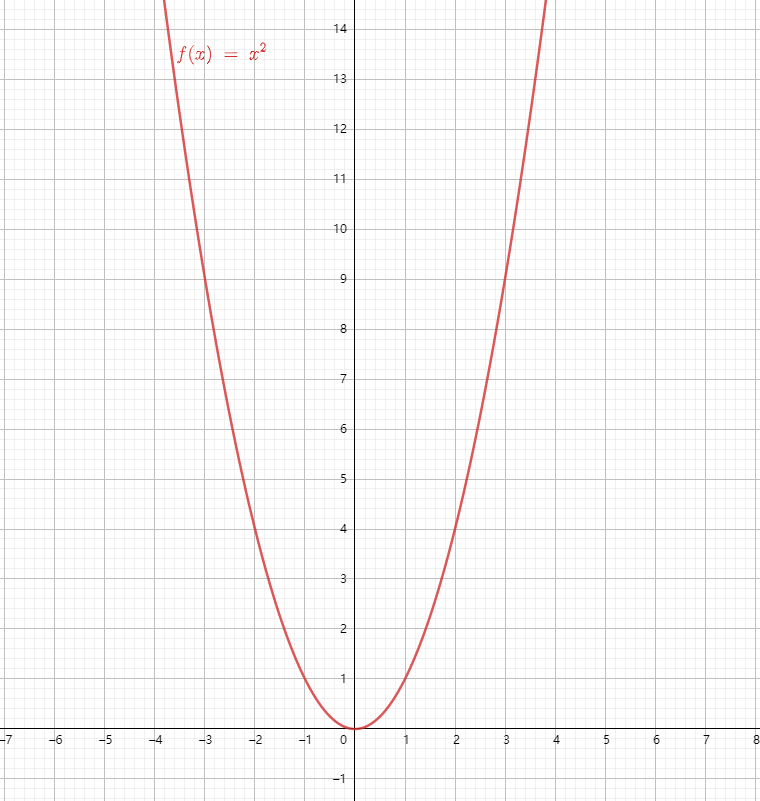
3 指数函数
3.1 基本概念
正整数指数幂
零指数幂
任何数的0次方都等于1
负整数指数幂
正分数指数幂
3.2 幂的运算法则
3.3 定义
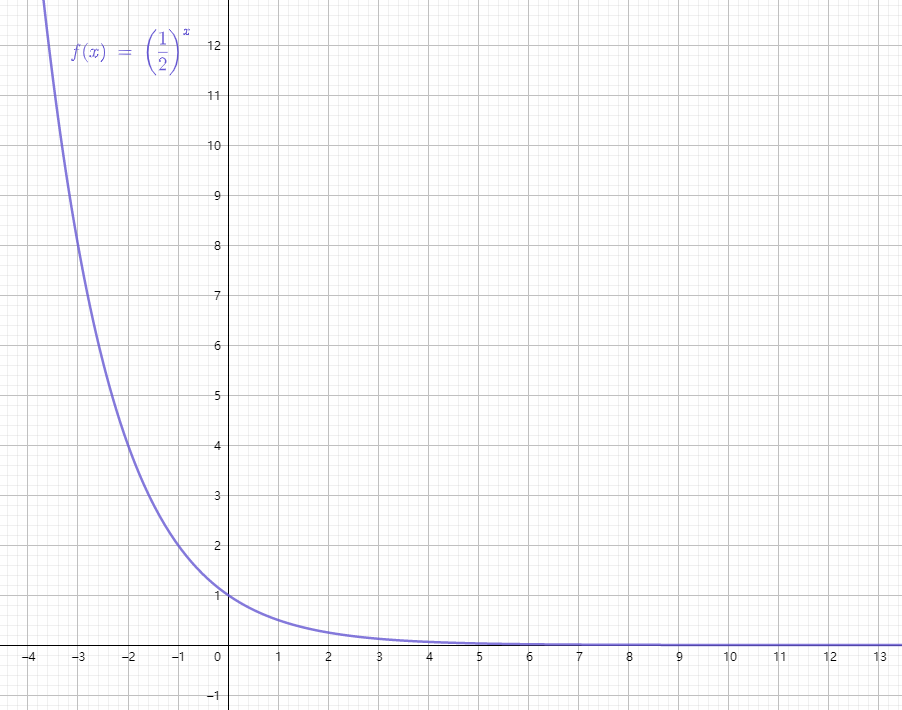
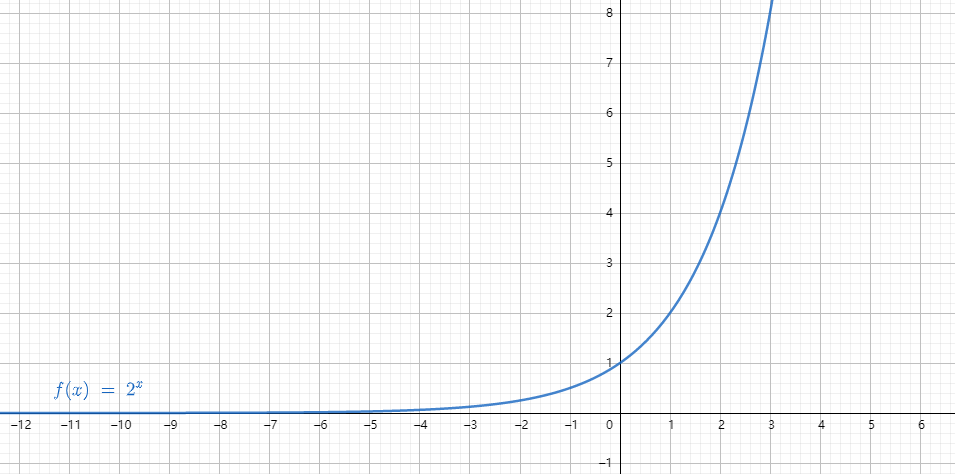
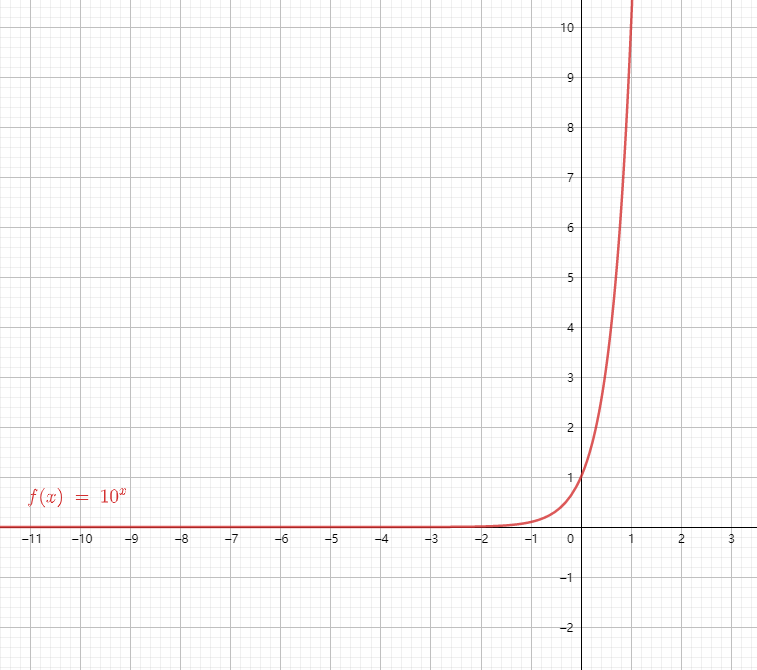
指数函数
当
当
时,指数函数没有实在意义,因为一个 值可能存在两个 值,不构成函数
常用的指数函数有
4 对数函数
4.1 基本概念
对数定义
如果
4.2 性质
0和负数无对数
将上面右变的值记作k,则
那么
,则
4.3 运算法则
-
这是
可以通过
一种
一种 -
上述相同,也是利用指数计算的性质
-
这里证明用到的是
换底公式没有讲
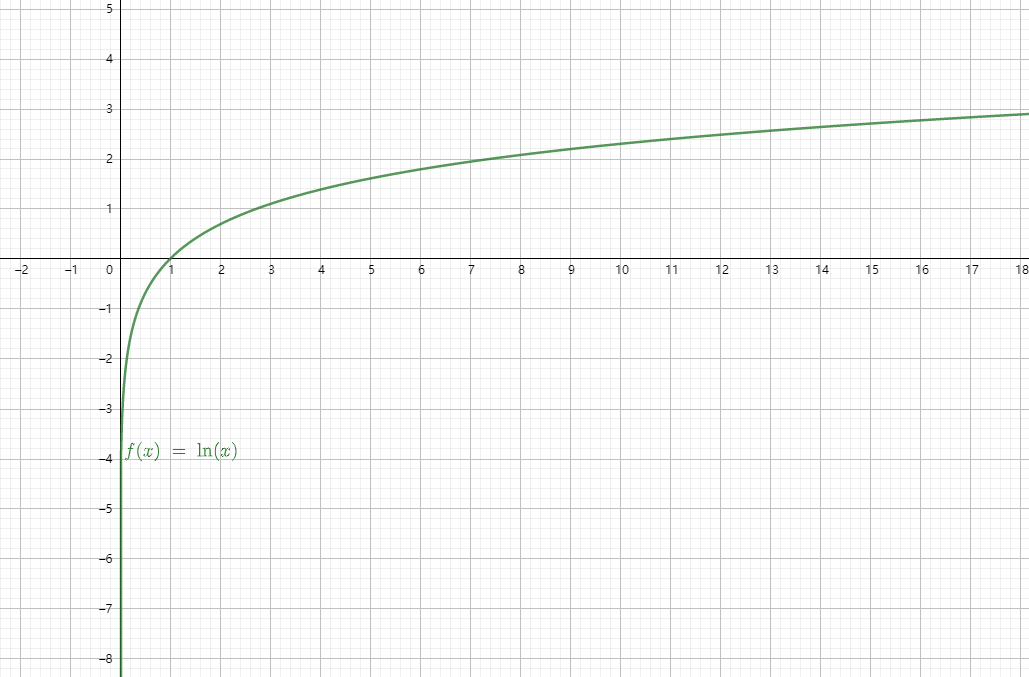
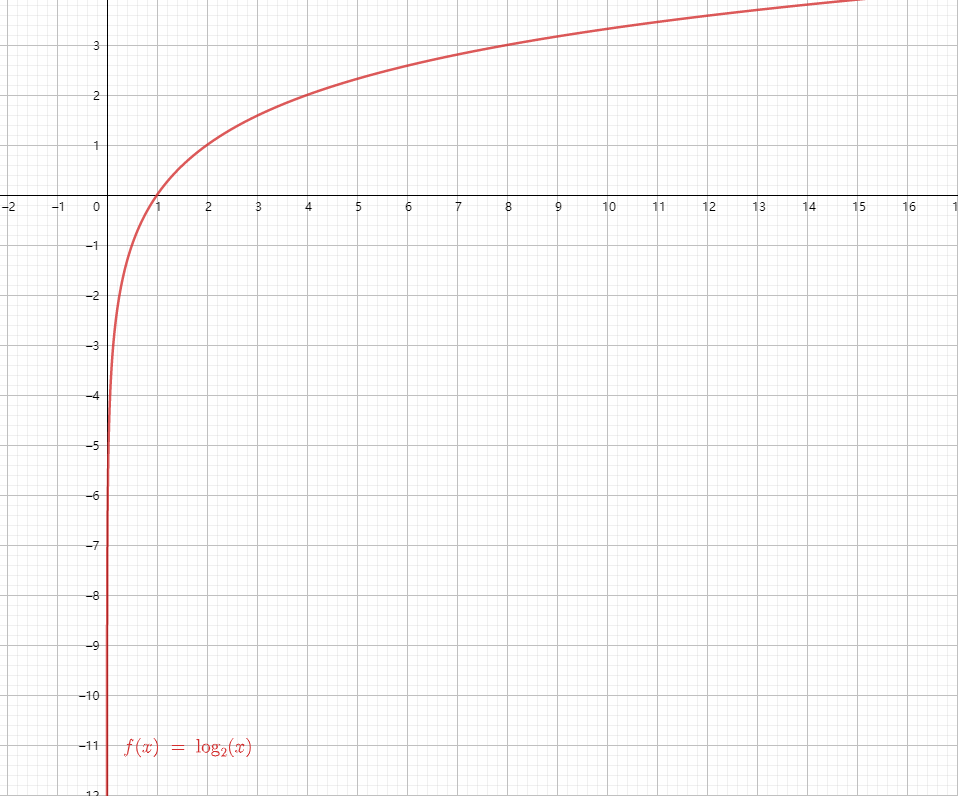
4.4 对数函数定义
对数函数
当
当
常用的对数函数有
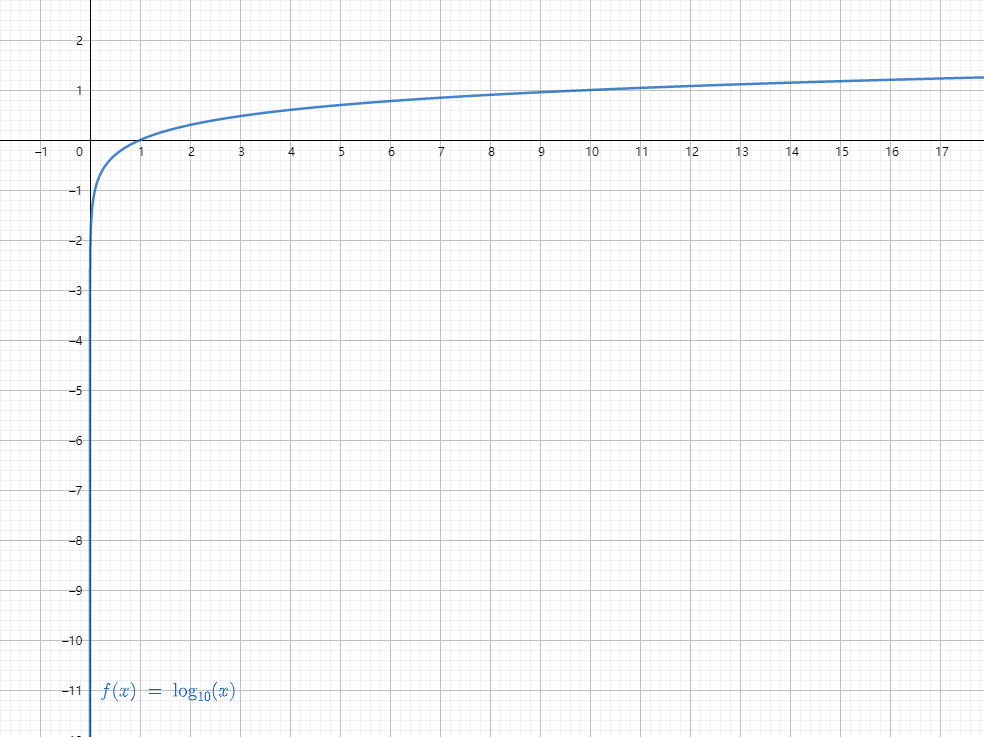
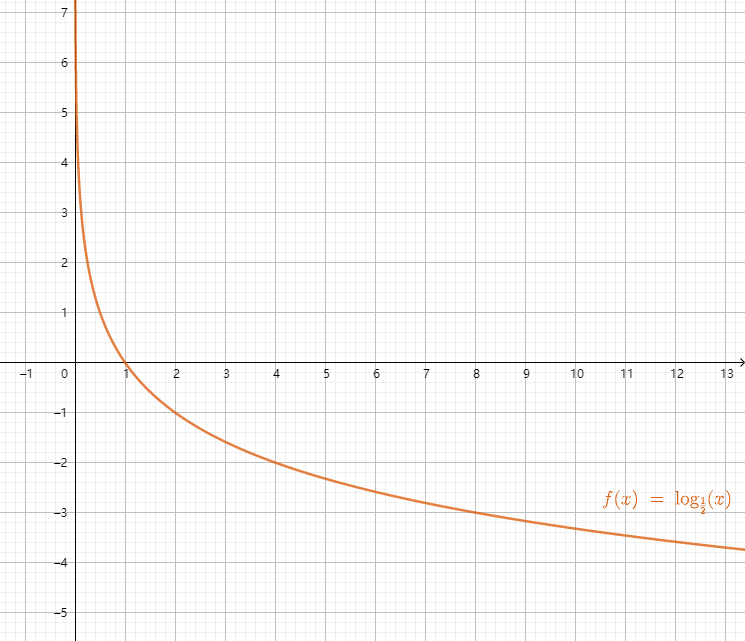
5 三角函数
5.1 角
正角,负角,零角
角可以看做是一条射线绕着它的端点在平面内旋转而成。逆时针(正角)
终边相同的角
象限角
在平面直角坐标系分为四象限,角度范围
第一象限 0° - 90°
第二象限 90° - 180°
第三象限 180° - 270°
第四象限 270° - 360°
角度和弧度的换算
单位圆是半径为1的圆 周长
弧度是角的度量单位,一段弧的长度叫做弧长
特殊的角度与弧度之间的对应关系
| 度 | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| 弧度 | 0 |
5.2 正弦函数
在直角三角形中,角度
一般的,在直角坐标系中,给定单位圆,对任意角α,使角α的顶点与原点重合,始边与x轴非负半轴重合,终边与单位圆交于点P(u,v),那么点P的纵坐标v叫做角α的正弦函数,记作v=sinα。通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角函数y=sin x,它的定义域为全体实数,值域为[-1,1]。
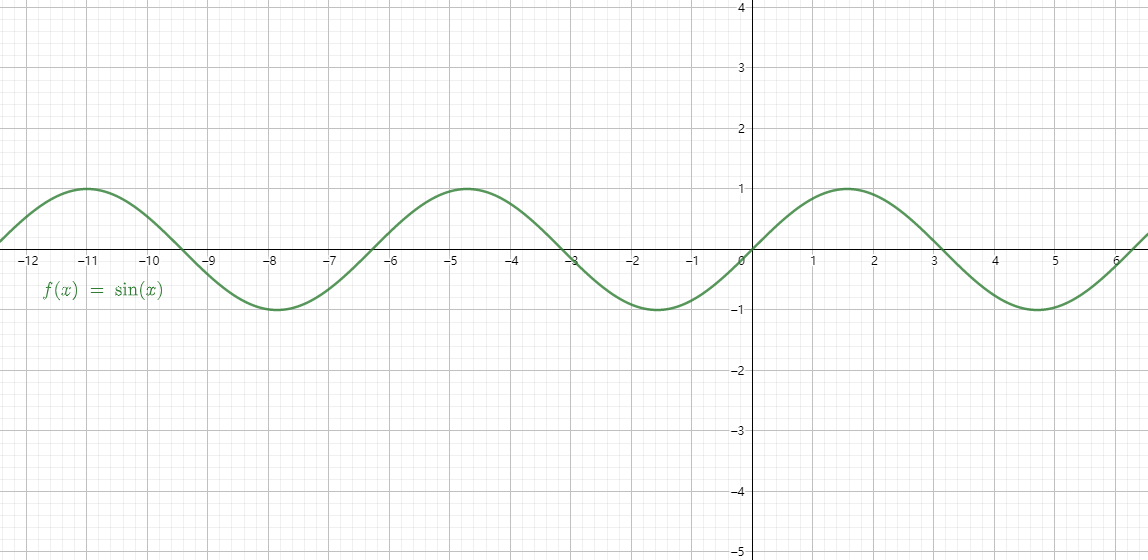
5.3 余弦函数
在直角三角形中,角度
一般的,在直角坐标系中,给定单位圆,对任意角α,使角α的顶点与原点重合,始边与x轴非负半轴重合,终边与单位圆交于点P(u,v),那么点P的横坐标u叫做角α的正弦函数,记作u=cosα。通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角函数y=cos x,它的定义域为全体实数,值域为[-1,1]。
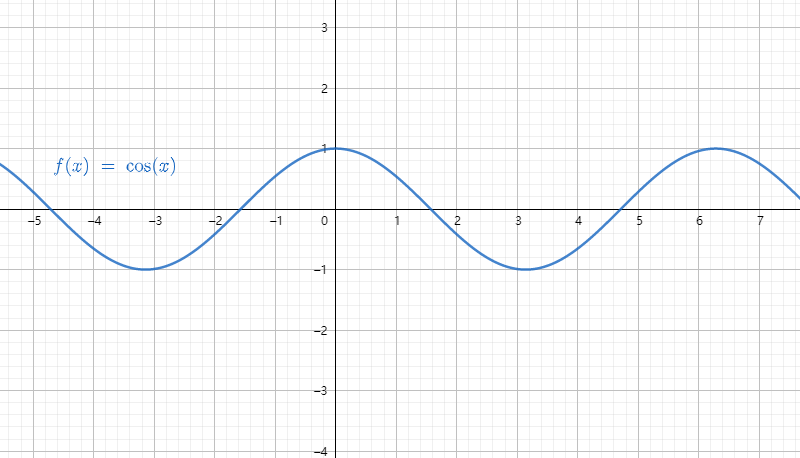
5.4 正切函数
正切就是正弦函数比余弦函数
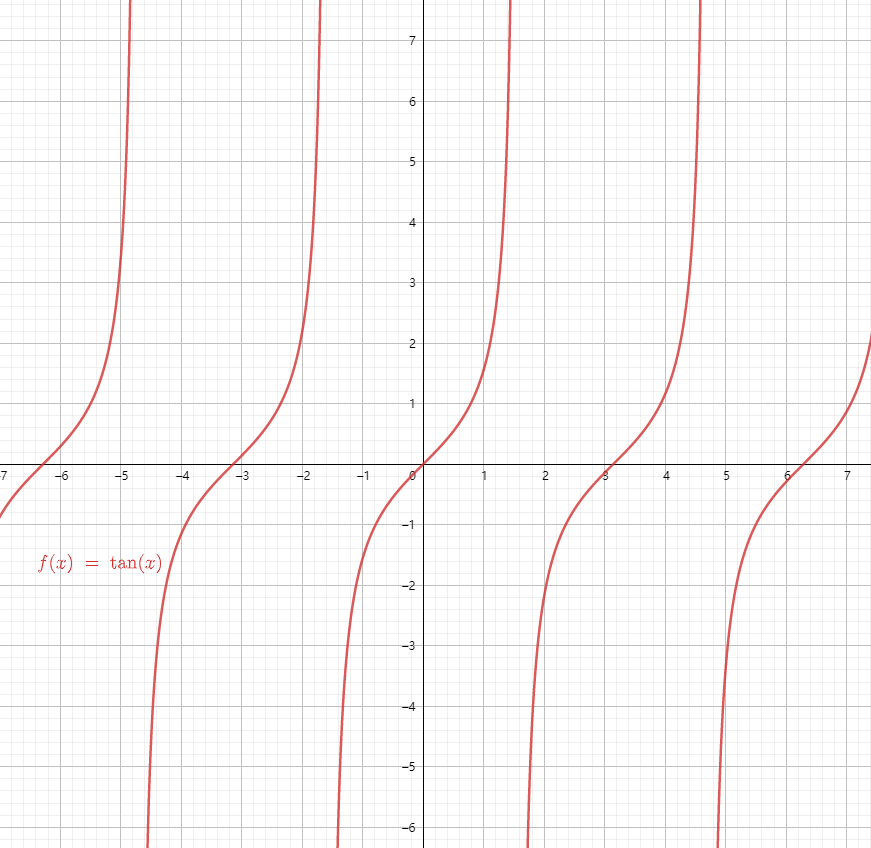
5.5 其他
余切函数
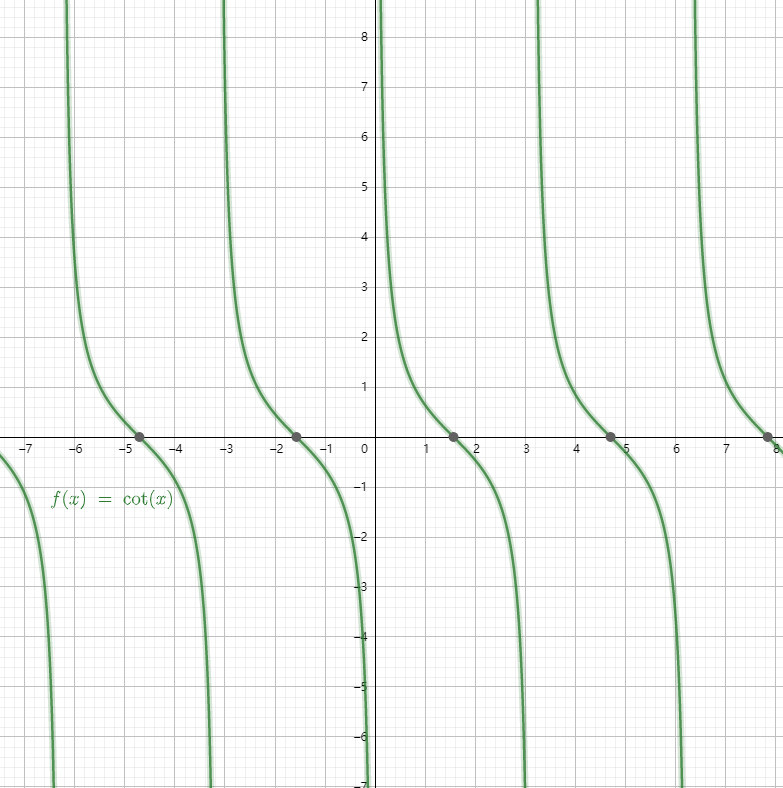
正割函数
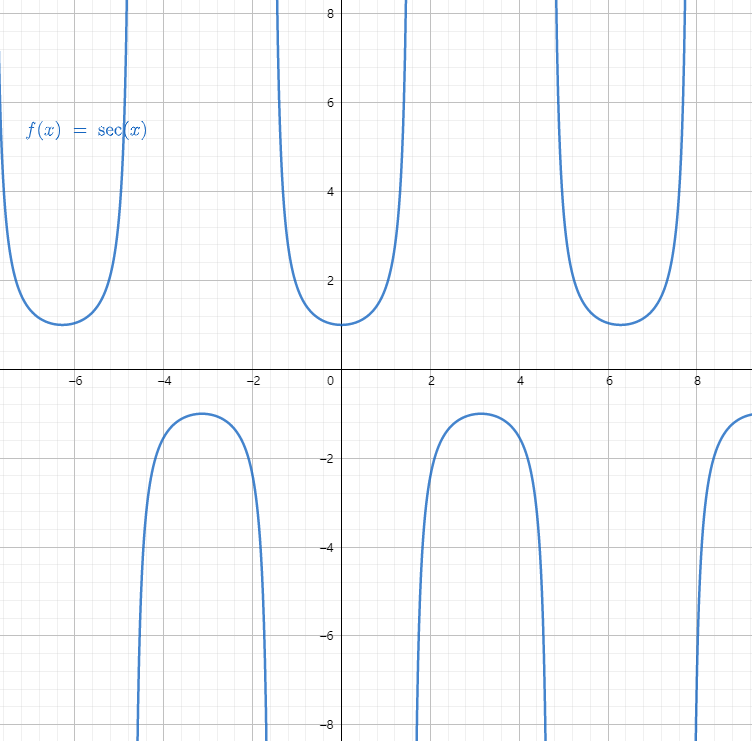
余割函数
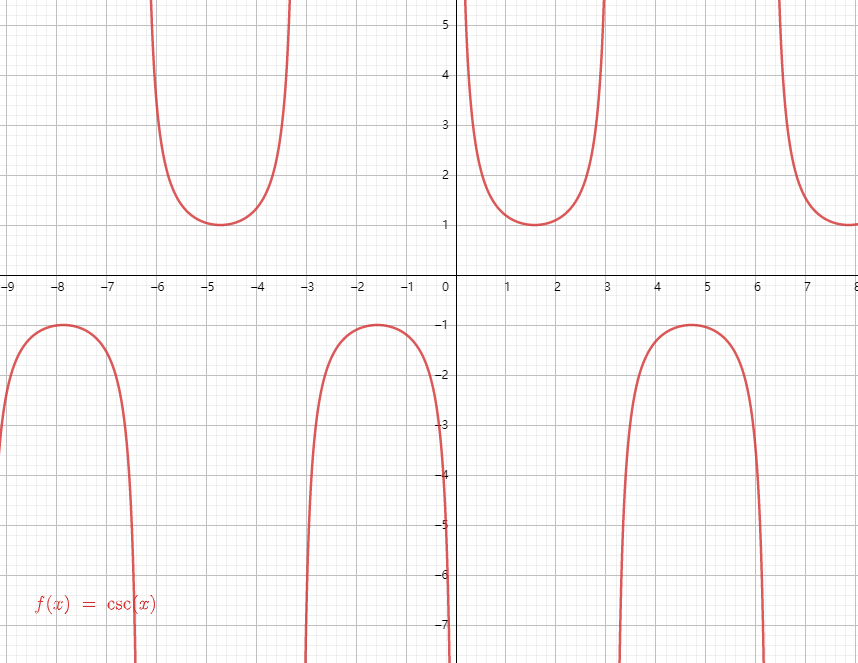
5.6 三角函数的值到底怎么来的
特殊的三角函数值
| 度 | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| 弧度 | ||||||||
正弦函数0到90度是
余弦函数0到90度是
5.7 同角三角函数的基本关系
1 倒数关系
2 商数关系
3 平方关系
5.8 诱导公式
函数名不变,符号看象限
5.9 两角和与差的三角函数
\alpha \beta
减法就是后面的变减号
减法就是后面的变加号
将
用到了
5.10 三角函数得图像
五点法作图
6 反三角函数
按照前面提到得反函数定义,三角函数都是周期函数,那么对于一个具体得函数值y会有无穷多个自变量x得值与之对应。按照函数得定义,x不是y的函数,也即三角函数在定义域内不存在反函数。但是,我们讲定义域在一定的范围之内,三角函数就存在反函数,也就是我们的反三角函数
6.1 反正弦函数
将正弦函数
此时,这是一个单调增加的函数,故它存在反函数,称为反正弦函数,记为
其定义域为
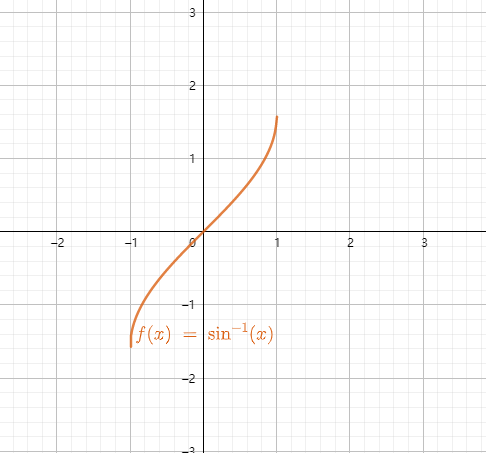
6.2 反余弦函数
定义域
值域
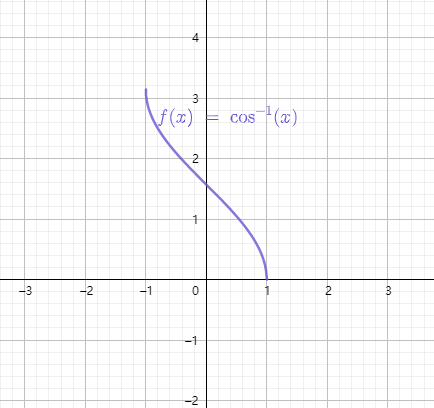
6.3 反正切函数
定义域 正无穷到负无穷
值域
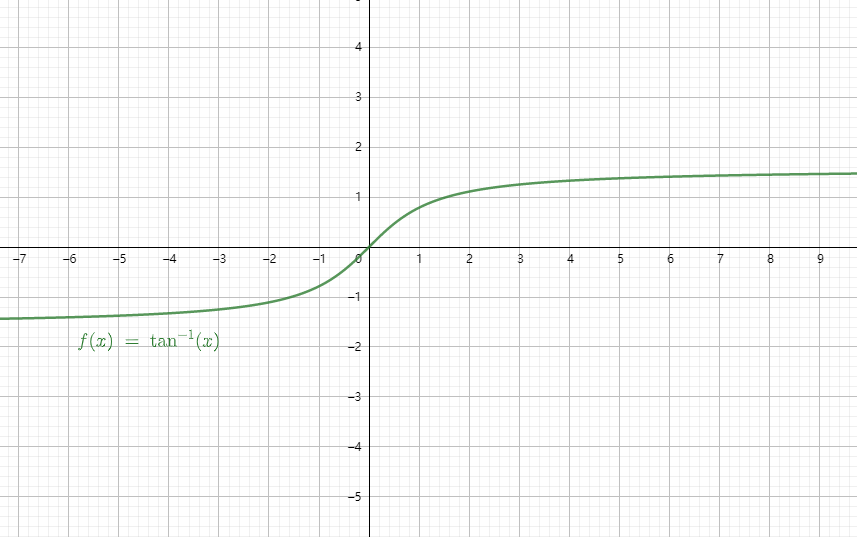




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律