数学基础02-集合、区间、函数、反函数和复合函数
集合
1 基本概念
1.1 定义
把一些确定的对象看成一个整体就形成了一个集合,集合一般用大写字母A B C ……表示
1.2 元素
集合中的每个对象叫做这个集合的元素,一般用a b c ……表示 (确定性,互异性,无序性)
1.3 元素和集合的关系
若
若
1.4 有限集和无限集
含有有限个元素的集合叫做有限集,含有无限个元素的集合叫做无限集
1.5 空集
不含有任何元素的集合叫做空集,记作
1.6 常用的几种数集及记号
| 自然数集 | 正整数集 | 正数集 | 有理数集 | 实数集 | 复数集 |
|---|---|---|---|---|---|
2 集合的表示方法
2.1 例举法
将集合中的元素一一例举出来并写在大括号内。
2.2 属性法
将集合中元素的共同特诊描述出来写在大括号内
2.3 图示法(韦恩氏图)
用封闭曲线的内部表示一个集合
3 集合与集合的关系
3.1 交集
由集合A与集合B的所有公共元素所组成的集合叫做A与B的交集,记作
3.2 并集
由集合
区间
1 定义
用“属性法”来表示数集的好处是它可以很方便的表示数轴上的 “一段” 连续的点,比如,由数轴上介于 1 与 2 之间的实数构成的数集可方便的表示为
像这样由数轴上的一段连续的点构成的数集我们称之为区间,记作
2 区间分类
常见的区间定义如下表,表中a,b是确定的实数。正负无穷大不代表任何数,仅仅是记号
| 名称 | 闭区间 | 开区间 | 左开右闭 | 左闭右开 | 正无穷区间 | 负无穷区间 | 无穷区间 |
|---|---|---|---|---|---|---|---|
| 记号 | |||||||
| 定义 |
函数
1 定义
设
判断是不是同一个函数
不是同一个函数,通过坐标系可以发现是4种不同的线。
函数例子
符号函数
气温函数
人口函数
分段函数,出租车收费
曲边三角形面积函数
2 表示方法
2.1 公式法
用数学公式表示因变量
2.2 图像法
用因变量
2.3 表格法
3 性质
函数的六大性质,只说明前4性质
3.1 有界性
定义:设函数
整个的定义域里面,不管
- 有界函数必有上界和下界;反之,既有上界又有下界的函数必是有界函数。只有一个界是不行的
- 界的无穷。函数有界则必定有无穷多个界
- 函数的有界性如何与自变量的
3.2 单调性
定义:设函数
负无穷到0,单调递减,0到正无穷,单调递增
例题
证明:函数
因为
3.3 奇偶性
定义:
设函数
成立,则称
成立,则称
由定义可知,偶函数的图像是关于
对定义域要求是关于原点对称的
加绝对值和偶次方都是偶函数
例题
1 讨论下列函数的奇偶性(4类)
2 证明:设函数
结论:设所考虑的函数都在
- 两个偶函数之和,之积为偶函数
- 两个奇函数之和为奇函数,之积为偶函数
- 一个奇函数与一个偶函数之积为奇函数
3.4 周期性
定义:设函数
成立,则称
3.5 连续性
3.6 凹凸性
4 反函数和复合函数
4.1 定义
概念引入
一个函数
定义
设函数
对于任何值域范围内的值在定义域范围内都有唯一确定的值一一对应,
随着 的改变而改变,这样 就是 的反函数。学会求反即可
例题(怎么求,反函数与原函数图像特点)
设函数
反函数
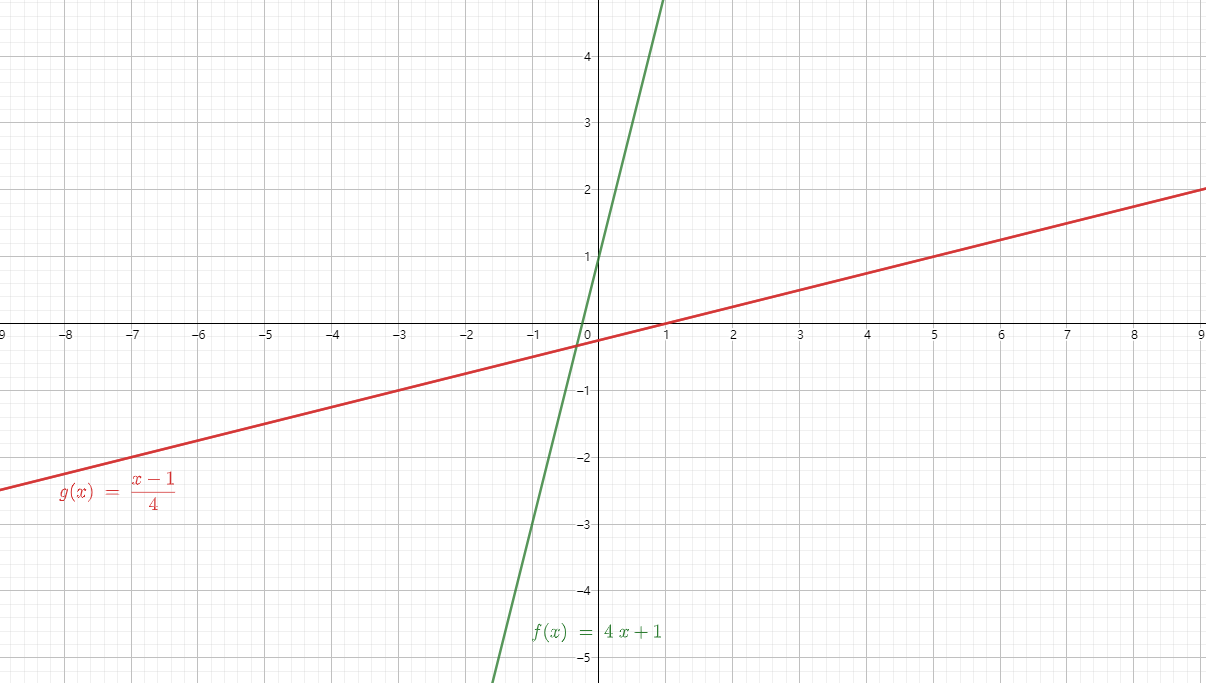
关于
这条线对称
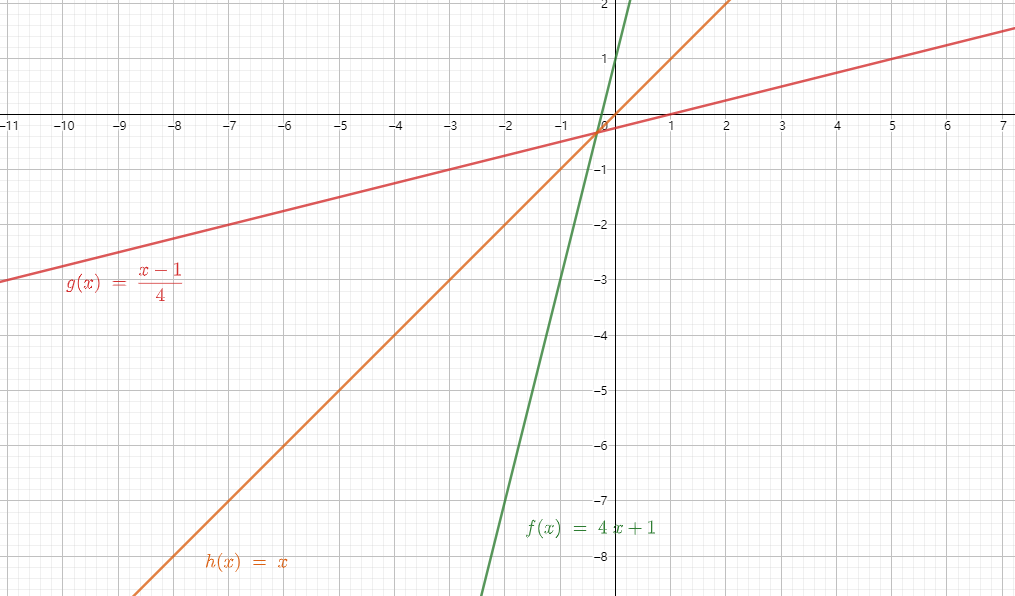
是不是所有的函数都有反函数呢?如果不是怎么限制条件
不是,
限制定义域确定有一个
4.2 复合函数
对函数
对函数
当尝试对多个函数进行复合时,突然发现内层函数的值域不在外层函数的定义域里面,函数就不能复合
如果有函数1和函数2,不能复合是指,函数2的值域不在函数1的定义域里面。
对函数
4.3 例题
求由
定义域为
设




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律