数学基础01-实数、式子、方程和方程组

目录

• 1. 实数
  • 1.1 分类
  • 1.2 相关的基本概念
    • 1.2.1 数轴
    • 1.2.2 绝对值
    • 1.2.3 相反数
    • 1.2.4 倒数
  • 1.3 实数的运算法则
    • 1.3.1 四则运算，加减乘除
    • 1.3.2 乘方
    • 1.3.3 开方
  • 1.4 实数的运算
    • 1.4.1 交换律
    • 1.4.2 结合律
    • 1.4.3 分配律
    • 1.4.4 运算顺序
• 2. 式子
  • 2.1 基本概念
  • 2.2 整式
    • 2.2.1 整式乘法运算
    • 2.2.2 整式乘法公式
      • 乘方差公式
      • 完全平方公式
    • 2.2.3 因式分解
      • 分解方法
        • 提取公因式
        • 配平方法
        • 十字相乘法
  • 2.3 分式
    • 2.3.1 定义
    • 2.3.2 性质
    • 2.3.3 运算
  • 2.4 二次根式
    • 2.4.1 定义
    • 2.4.2 性质
    • 2.4.3 运算
    • 2.4.4 分母有理化
• 3. 方程和方程组
  • 3.1 基本概念
  • 3.2 一元一次方程
  • 3.2 一元二次方程
    • 3.2.1 解方程的方法
      • 配方法
      • 因式分解
      • 求根公式
  • 3.3 方程组
  • 3.4 例题
    • 例1 $|\sqrt{a}-1| = $
    • 例2 关于 \(y\) 的方程 \(y^2 + my -m = 0\) 有两个不相等的实数根，求m的取值范围
    • 例3 若\(x+y = 3,y+z=4,z+x=5\),求\(x,y,z\)的值
    • 例4 若\(|m+2|\) 与 \(n^2-8n+16\) 互为相反数，则\((x^2+y^2)-(mxy+n)=\)
    • 例5 已知\(x^2 - 4x +1 = 0\),则 \(x - \frac{1}{x}=\)

1. 实数

1.1 分类

实数分类

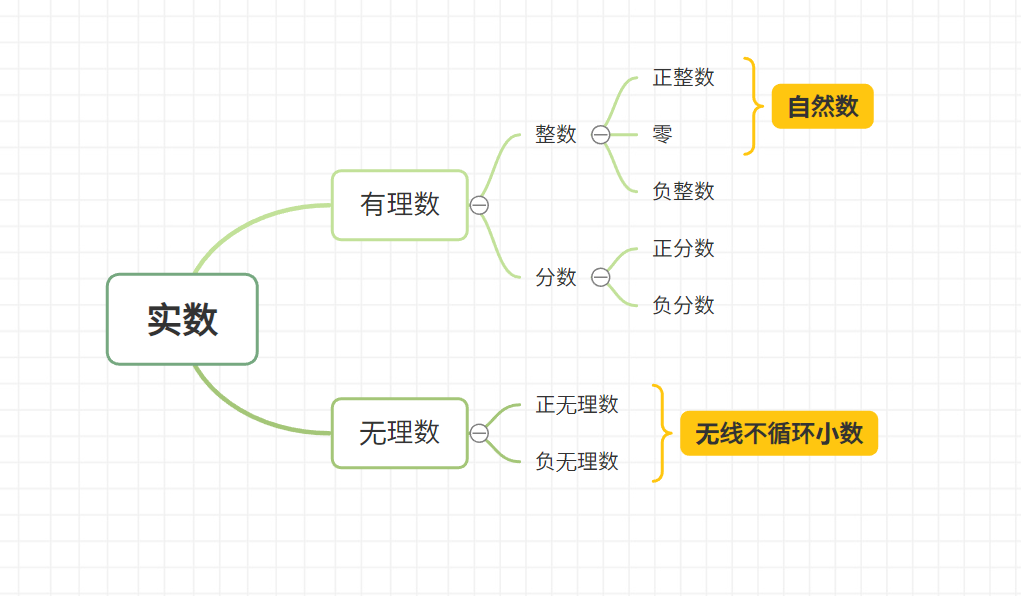
1.2 相关的基本概念

1.2.1 数轴

在数学中，可以用一条直线上的点表示数，这条直线 叫做数轴，包含原点，正方向，单位长度并于实数一一对应。

1.2.2 绝对值

正数绝对值是它本身，负数绝对值是它相反数

1.2.3 相反数

绝对值相同但是符号相反的两个数，两个数在数轴中到原点的距离相等，则他们互为相反数。

1.2.4 倒数

1除以某数的商叫做倒数，0没有倒数

1.3 实数的运算法则

1.3.1 四则运算，加减乘除

1.3.2 乘方

1. 正数的任何次幂都是正数，负次幂等于该数倒数的正次幂。

​ $$n^{-m} = \frac{1}{n^m}$$

​ \(n^{-m} = n^{0-m} = \frac{n^0}{n^m} = (\frac{1}{n})^m = \frac{1}{n^m}\)

2. 负数的偶次幂是正数，奇次幂是负数

3. 任何不为0的数的0次幂都为1

   \[a^0 = 1 \]

   \(a^0 = a^{n-n} = \frac{a^n}{a^n} = 1\)

4. 0的正数次幂都为0，非正数次幂无意义，因为0不能做分母

5. 任何不等于0的-p次幂都等于这个数的p次幂的倒数

   \[a^{-p} \times a^p = a^0 = 1 \]
   \[a^{-p} = \frac{1}{a^p} \]

1.3.3 开方

一个正数有两个平方根，他们互为相反数，0的平方根是0
\(\sqrt{4} = 2\)
负数没有平方根
一个正数有一个正的立方根，一个负数有一个负的立方根，0的立方根为0

1.4 实数的运算

1.4.1 交换律

\[a + b = b + a \tag{交换律} \]

1.4.2 结合律

\[a+(b+c) = (a+b)+c\tag{结合律} \]

1.4.3 分配律

\[a\times(b+c) = a\times b+a\times c\tag{分配律} \]

1.4.4 运算顺序

先乘方，开方，然后乘除，最后加减，有括号先算括号。

2. 式子

2.1 基本概念

用运算符号将数字或表示数字的字母连接起来的式子叫做代数式
数值代入计算的结果表示代数式的值

2.2 整式

2.2.1 整式乘法运算

\[a^m \times a^n = a^{m + n} \]

\[(a^m)^n = a^{m \times n} \]

\[a^m \div a^n = a^{m-n} \]

\[(a \times b)^n = a^n \times b^n \]

2.2.2 整式乘法公式

乘方差公式

\[(a+b)\times(a-b) = a^2 - b^2 \tag{乘方差公式} \]

完全平方公式

\[(a \pm b)^2 = a^2 \pm 2ab + b^2 \tag{完全平方公式} \]

\[a^2 + 2ab = a^2 + 2ab + b^2 - b^2 = (a+b)^2 - b^2 \]

2.2.3 因式分解

把一个多项式化成几个整式的积的形式叫做因式分解

分解方法

提取公因式

\[2ab^2 + a^2b = ab(2b+a) \]

配平方法

$
x^2 + 4x + 3 \
= x^2 + 2 \times 2x + 2^2 - 2^2 + 3\
= (x+2)^2 - 2^2 +3\
= (x+2)^2 - 1^2\
= (x+2+1)(x+2-1)\
= (x+3)(x+1) $

十字相乘法

将二次项和常数项因式分解，用十字相乘再加等于中间项
$ x^2 + 14x + 45 = (x+5)(x+9) $

2.3 分式

2.3.1 定义

设A，B表示两个整式，形如\(\frac{A}{B}(B \neq 0)\)的式子叫做分式

2.3.2 性质

\[\frac{A}{B} = \frac{A \times N}{B \times N}(N \neq 0) \]

\[\frac{A}{B} = \frac{A \div N}{B \div N} \]

2.3.3 运算

\[\frac{a}{b} \pm \frac{c}{d} = \frac{ad}{bd} \pm \frac{cb}{bd} = \frac {ad \pm cb}{bd} \]

\[\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd} \]

\[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{ad}{bc} \]

2.4 二次根式

2.4.1 定义

式子\(\sqrt a(a \geq 0)\)叫做二次根式，偶次方根必须大于0

2.4.2 性质

\[(\sqrt a)^2 = a(a \geq 0) \]

\[\sqrt{a^2} = |a| \begin{cases} a(a \geq 0)\\ -a(a < 0)\\ \end{cases} \]

2.4.3 运算

\[\sqrt a \times \sqrt b = \sqrt {ab}(a \geq 0,b \geq 0) \]

\[\frac{\sqrt a}{\sqrt b} = \sqrt \frac{a}{b} (a \geq 0,b>0) \]

2.4.4 分母有理化

化去分母的根号叫做分母的有理化
\( \frac {1}{\sqrt 2} = \frac{1 \times \sqrt 2}{\sqrt 2 \times \sqrt 2} = \frac {\sqrt 2}{2} \)

\[\frac {1}{\sqrt a} = \frac {\sqrt a}{a} \]

\( \frac {1}{\sqrt 3 + \sqrt 2}\\ = \frac {\sqrt 3 - \sqrt 2}{(\sqrt 3 + \sqrt 2)(\sqrt 3 - \sqrt 2)}\\ = \frac {\sqrt 3 - \sqrt 2}{(\sqrt 3)^2-(\sqrt 2)^2}\\ = \sqrt 3 - \sqrt 2 \)

3. 方程和方程组

3.1 基本概念

含有未知数的等式叫做方程
使方程左右两边相等的未知数的值叫做方程的解
求未知数值得过程叫做解方程

3.2 一元一次方程

一个未知数，最高次为1的方程

\[ax+b=0(a \neq 0) \tag{一元一次方程}\\ ax=-b\\ x=-\frac{b}{a} \]

3.2 一元二次方程

一个未知数，最高次为2的方程

\[ax^2 + bx +c = 0 (a \neq 0)\tag{一元二次方程}\\ \]

3.2.1 解方程的方法

配方法

将式子匹配成完全平方公式再进行解

因式分解

提取公共部分再解

求根公式

\[\Delta = b^2 - 4ac\tag{判别式}\\ \]

当\(\Delta>0\)时，有两个不相等的实数根
当\(\Delta=0\)时，有两个相等的实数根
当\(\Delta<0\)时，没有实数根

\[x = \frac{-b\pm \sqrt{b^2-4ac}}{2a} \tag{求根公式}\\ \]

\[\begin{align*} ax^2 + bx + c &= 0\\ \tag{推导过程} ax^2 + bx &= -c \\ x^2 + \frac{b}{a} \times x &= - \frac{c}{a} \\ x^2 + 2\frac{b}{2a} + (\frac{b}{2a})^2 &= (\frac{b}{2a})^2-\frac{c}{a} \\ (x + \frac{b}{2a})^2 &= \frac{b^2}{4a^2} - \frac{c}{a} \\ (x + \frac{b}{2a})^2 &= \frac{b^2}{4a^2} - \frac{4ac}{4a^2} = \frac{b^2-4ac}{4a^2} \\ x + \frac{b}{2a} &= \sqrt{\frac{b^2-4ac}{4a^2}} = \frac{\pm \sqrt{b^2-4ac}}{\sqrt{4a^2}} \\ x + \frac{b}{2a} &= \frac{\pm \sqrt{b^2-4ac}}{2a} \\ x &= -\frac{b}{2a} + \frac{\pm \sqrt{b^2-4ac}}{2a} \\ x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a} \end{align*}\]

根与系数的关系

\[x_1 + x_2 = -\frac{b}{a}\\ x_1 \times x_2 = \frac{c}{a} \]

3.3 方程组

由几个方程连立起来组成的一组方程叫做方程组
常用解法是代入消元法

\[\begin{cases} a_1x + b_1y + c_1 = 0\\ \tag{二元一次方程组} a_2x + b_2y + c_2 = 0 \end{cases} \]

3.4 例题

例1 $|\sqrt{a}-1| = $

求绝对值的值，很显然，有正负两个值，解开就得到两个结果
\( |\sqrt a-1| = \pm \sqrt {a}-1 = \begin{cases} \sqrt{a}-1\\ -(\sqrt{a}-1) = - \sqrt a + 1 = 1 - \sqrt a \end{cases} \)

例2 关于 \(y\) 的方程 \(y^2 + my -m = 0\) 有两个不相等的实数根，求m的取值范围

因为该一元二次方程有两个不相等的实数根，则 \(\Delta > 0\)，那么根据判定式可知
\( \because \Delta = b^2 -4ac = m^2 - 4 \times 1 \times -m = m^2 + 4m = m(m+4) > 0 \\ \therefore \begin{cases} m>0,m+4>0\\ m<0,m+4<0 \end{cases}\\ \begin{cases} m>0,m>-4 ; m>0\\ m<0,m+4<0; m < -4 \end{cases} \)
使用了提取公因式得到\(m(m+4)\),所以m的取值范围为\(m>0,m<-4\)

例3 若\(x+y = 3,y+z=4,z+x=5\),求\(x,y,z\)的值

\( x+y+y+z+z+x=3+4+5\\ 2x+2y+2z = 12 \\ x+y+z = 6 \\ x + 4 = 6, x = 2 \\ y + 5 = 6, y = 1 \\ z + 3 = 6, z = 3 \\ \)

例4 若\(|m+2|\) 与 \(n^2-8n+16\) 互为相反数，则\((x^2+y^2)-(mxy+n)=\)

因为他们互为相反数，则和为0
\( |m+2| + n^2-8n+16 = 0\\ |m+2| + (n-4)^2 = 0\\ m+2 =0,n-4 = 0\\ m = -2,n = 4\\ \\ (x^2+y^2)-(mxy+n) \\ = (x^2+y^2)-(-2xy+4) \\ = x^2+y^2 + 2xy - 4 \\ = (x+y)^2 - 4\\ = (x+y)^2 - 2^2\\ = (x+y+2) \times (x+y-2) \)

例5 已知\(x^2 - 4x +1 = 0\),则 \(x - \frac{1}{x}=\)

将\(x^2 - 4x +1 = 0\)等式两边除以\(x\),则
\( x-4+ \frac{1}{x} = 0\\ x + \frac{1}{x} = 4\\ (x+(\frac{1}{x})^2 = 4^2\\ x^2 + 2 + (\frac{1}{x})^2 = 16\\ x^2 + (\frac{1}{x})^2 = 14 \)

\( (x - \frac{1}{x})^2\\ = x^2 - 2 + (\frac{1}{x})^2\\ = 14 - 2 \\ = 12 \)

\( x - \frac{1}{x} \\ = \sqrt{12} \\ = \sqrt{4 \times 3} \\ = \sqrt4 \times \sqrt 3 \\ = \pm2 \sqrt3 \)