Lucas-Kanade算法总结
Lucas-Kanade算法广泛用于图像对齐、光流法、目标追踪、图像拼接和人脸检测等课题中。
一、核心思想
给定一个模板 和一个输入
和一个输入 ,以及一个或多个变换
,以及一个或多个变换 ,求一个参数最佳的变换
,求一个参数最佳的变换 ,使得下式最小化
,使得下式最小化

在求最优解的时候,该算法假设目前的变换参数 已知,并迭代的计算
已知,并迭代的计算 的增量
的增量 ,使得更新后的
,使得更新后的 能令上式比原来更小。则上式改写为:
能令上式比原来更小。则上式改写为:

二、算法流程
1.初始化参数向量
2.计算 及其关于
及其关于 导数,求得参数增量向量
导数,求得参数增量向量
3.更新 ,
,
4.若 小于某个小量,即当前参数向量
小于某个小量,即当前参数向量 基本不变化了,那么停止迭代,否则继续2,3两步骤。
基本不变化了,那么停止迭代,否则继续2,3两步骤。
三、具体做法
对 做一阶泰勒级数展开,则目标函数变为:
做一阶泰勒级数展开,则目标函数变为:

对其求导,并令导数为0,得到下式:

对上式中的 求解即可,得到的是
求解即可,得到的是 的解析解:
的解析解:

其中,

四、Lucas-Kanade算法(前向加性算法)
迭代:
1) 利用 ,将
,将 中各个像素点的坐标对应到
中各个像素点的坐标对应到 中的相应的像素点的坐标,得到
中的相应的像素点的坐标,得到 。即
。即 和的
和的 大小尺寸(像素个数和长宽)相同。
大小尺寸(像素个数和长宽)相同。
2) 计算 ,获得误差图像。
,获得误差图像。
3) 计算 中与
中与 经过
经过 变换对应的像素点的梯度图像
变换对应的像素点的梯度图像 ,即计算
,即计算 中各个点在
中各个点在 中的梯度。利用
中的梯度。利用 ,将
,将 中各个像素点的坐标对应到
中各个像素点的坐标对应到 的梯度图像
的梯度图像 中各个点的坐标。
中各个点的坐标。
4) 计算在 设定下的Jacobian
设定下的Jacobian 。即代入当前参数
。即代入当前参数 ,计算
,计算 。如果
。如果 是二维坐标,即
是二维坐标,即 ,也就是说每行是对
,也就是说每行是对 中每个分量对于
中每个分量对于 的每个参数分量的导数:
的每个参数分量的导数:

5) 计算最速梯度下降图 。即利用
。即利用 与
与 中每个像素点相乘。
中每个像素点相乘。
6) 利用上述提到的公式计算Hessian矩阵
7) 利用上面步骤计算得到的值,计算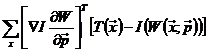
8) 利用上述提到的公式计算参数向量的增量
9) 更新 ,
,
五、Baker-Matthews算法(逆向组成算法)
预处理:
1) 计算模板 的梯度图像
的梯度图像
2) 计算在 设定下的Jacobian
设定下的Jacobian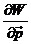
3) 计算最速梯度下降图 。即利用
。即利用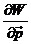 与
与 中每个像素点相乘。
中每个像素点相乘。
4) 利用公式计算Hessian矩阵
迭代:
5) 利用 ,将
,将 中各个像素点的坐标对应到
中各个像素点的坐标对应到 中的相应的像素点的坐标,得到
中的相应的像素点的坐标,得到 。即
。即 和
和 的大小尺寸(像素个数和长宽)相同。
的大小尺寸(像素个数和长宽)相同。
6) 计算 ,获得误差图像。
,获得误差图像。
7) 利用上面步骤计算得到的值,计算
8) 利用上述提到的公式计算参数向量的增量
9) 更新 ,
, 。即将原有
。即将原有 的矩阵与
的矩阵与 矩阵的逆相乘。
矩阵的逆相乘。
六、参考文献和资料
[1]Matthews I, Baker S. Active appearance models revisited[J]. International Journal of Computer Vision, 2004, 60(2): 135-164.
[2]Cootes T F, Edwards G J, Taylor C J. Active appearance models[J]. IEEE Transactions on pattern analysis and machine intelligence, 2001, 23(6): 681-685.
[3]Baker S, Matthews I. Lucas-kanade 20 years on: A unifying framework[J]. International Journal of Computer Vision, 2004, 56(3): 221-255.
[4]利用L-K算法实现的图像对齐程序:http://www.codeproject.com/Articles/24809/Image-Alignment-Algorithms



 浙公网安备 33010602011771号
浙公网安备 33010602011771号