二叉树问题

题目描述

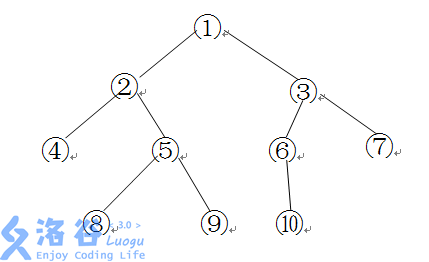
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

输入格式

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

输出格式

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

输入输出样例

输入 #1复制

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出 #1复制

4
4
8

经过剖析样例，我微微思索手动模拟后发现 要找最近的公共祖先，一次次地向上找就好了嘛，其实这有点并查集地意思

寻找时可分为两种情况
1.两点在不同子树中，有公共祖先
2.其中一个点是另一个的祖先

那么代码可以这么写

谁在下面谁就向上走，u向上时用depp1记录，v向上时depp2记录

 

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
int next[100040];
int to[100040];
int st[1000040];
int de[100040];
int dn[100040];
int ru[100040];
int fa[100040][50];
int n,k,tot=0;
void add(int x,int y)
{
    to[++tot]=y;
    next[tot]=st[x];
    st[x]=tot;
}
void build(int num,int fath)
{
    de[num]=de[fath]+1;
    dn[de[num]-1]++;
    fa[num][0]=fath;
    for(int i=1;i<=29;i++)
    fa[num][i]=fa[fa[num][i-1]][i-1];
    for(int i=st[num];i;i=next[i])
    if(to[i]!=fath) build(to[i],num);
}
int LCA(int x,int y)
{
    if(de[x]<de[y])
    {
        int u=x;
        x=y;
        y=u;
    }
    for(int i=30;i>=0;i--)
    {
        if(de[fa[x][i]]>=de[y]) x=fa[x][i];
        if(x==y) return x;
    }
    for(int i=30;i>=0;i--)
    if(fa[x][i]!=fa[y][i])
    {
        x=fa[x][i];
        y=fa[y][i];
    }
    return fa[x][0];
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n-1;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(y,x);
        add(x,y);
    }
    build(1,0);
    int ma=0;
    for(int i=1;i<=n;i++)
    if(de[i]>ma)
    ma=de[i];
    printf("%d\n",ma);
    int lo=0;
    for(int i=1;i<=ma;i++)
    if(dn[i]>lo)
    lo=dn[i];
    printf("%d\n",lo);
    int x,y;
    scanf("%d%d",&x,&y);
    printf("%d\n",2*(de[x]-de[LCA(x,y)])+de[y]-de[LCA(x,y)]);
    return 0;
}