Codeforces Round #270 A~D
One way to create a task is to learn from math. You can generate some random math statement or modify some theorems to get something new and build a new task from that.
For example, there is a statement called the "Goldbach's conjecture". It says: "each even number no less than four can be expressed as the sum of two primes". Let's modify it. How about a statement like that: "each integer no less than 12 can be expressed as the sum of two composite numbers." Not like the Goldbach's conjecture, I can prove this theorem.
You are given an integer n no less than 12, express it as a sum of two composite numbers.
The only line contains an integer n (12 ≤ n ≤ 106).
Output two composite integers x and y (1 < x, y < n) such that x + y = n. If there are multiple solutions, you can output any of them.
12
4 8
15
6 9
23
8 15
1000000
500000 500000
In the first example, 12 = 4 + 8 and both 4, 8 are composite numbers. You can output "6 6" or "8 4" as well.
In the second example, 15 = 6 + 9. Note that you can't output "1 14" because 1 is not a composite number.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
bool isp[1001000];
void get_prime()
{
isp[1]=isp[0]=true;
for(int i=2;i<=1000010;i++)
{
if(isp[i]==false)
for(int j=i*2;j<=1000010;j+=i)
isp[j]=true;
}
}
int main()
{
get_prime();
int n;
scanf("%d",&n);
int x,y;
for(int i=2;i<=n;i++)
{
if(isp[i]==true&&isp[n-i]==true)
{
printf("%d %d\n",i,n-i);
return 0;
}
}
return 0;
}One way to create a task is to learn from life. You can choose some experience in real life, formalize it and then you will get a new task.
Let's think about a scene in real life: there are lots of people waiting in front of the elevator, each person wants to go to a certain floor. We can formalize it in the following way. We have n people standing on the first floor, the i-th person wants to go to the fi-th floor. Unfortunately, there is only one elevator and its capacity equal to k (that is at most k people can use it simultaneously). Initially the elevator is located on the first floor. The elevator needs |a - b| seconds to move from the a-th floor to the b-th floor (we don't count the time the people need to get on and off the elevator).
What is the minimal number of seconds that is needed to transport all the people to the corresponding floors and then return the elevator to the first floor?
The first line contains two integers n and k (1 ≤ n, k ≤ 2000) — the number of people and the maximal capacity of the elevator.
The next line contains n integers: f1, f2, ..., fn (2 ≤ fi ≤ 2000), where fi denotes the target floor of the i-th person.
Output a single integer — the minimal time needed to achieve the goal.
3 2 2 3 4
8
4 2 50 100 50 100
296
10 3 2 2 2 2 2 2 2 2 2 2
8
In first sample, an optimal solution is:
- The elevator takes up person #1 and person #2.
- It goes to the 2nd floor.
- Both people go out of the elevator.
- The elevator goes back to the 1st floor.
- Then the elevator takes up person #3.
- And it goes to the 2nd floor.
- It picks up person #2.
- Then it goes to the 3rd floor.
- Person #2 goes out.
- Then it goes to the 4th floor, where person #3 goes out.
- The elevator goes back to the 1st floor.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,k;
int f[2200];
int all[2200];
int main()
{
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)
{
scanf("%d",f+i);
all[f[i]]++;
}
int now=0,high=1,ans=0;
for(int i=2000;i>=1;(all[i]==0)?i--:i+=0)
{
if(all[i])
{
if(now==0) high=i;
if(now+all[i]<=k)
{
now+=all[i];
all[i]=0;
}
else /// now + all[i]>k
{
int res=k-now;
all[i]-=res;
now=k;
}
}
if(now==k||i==1)
{
ans+=(high-1)*2;
now=0;high=1;
}
}
printf("%d\n",ans);
return 0;
}A way to make a new task is to make it nondeterministic or probabilistic. For example, the hard task of Topcoder SRM 595, Constellation, is the probabilistic version of a convex hull.
Let's try to make a new task. Firstly we will use the following task. There are n people, sort them by their name. It is just an ordinary sorting problem, but we can make it more interesting by adding nondeterministic element. There are n people, each person will use either his/her first name or last name as a handle. Can the lexicographical order of the handles be exactly equal to the given permutation p?
More formally, if we denote the handle of the i-th person as hi,
then the following condition must hold: 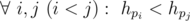 .
.
The first line contains an integer n (1 ≤ n ≤ 105) — the number of people.
The next n lines each contains two strings. The i-th line contains strings fi and si (1 ≤ |fi|, |si| ≤ 50) — the first name and last name of the i-th person. Each string consists only of lowercase English letters. All of the given 2n strings will be distinct.
The next line contains n distinct integers: p1, p2, ..., pn (1 ≤ pi ≤ n).
If it is possible, output "YES", otherwise output "NO".
3 gennady korotkevich petr mitrichev gaoyuan chen 1 2 3
NO
3 gennady korotkevich petr mitrichev gaoyuan chen 3 1 2
YES
2 galileo galilei nicolaus copernicus 2 1
YES
10 rean schwarzer fei claussell alisa reinford eliot craig laura arseid jusis albarea machias regnitz sara valestin emma millstein gaius worzel 1 2 3 4 5 6 7 8 9 10
NO
10 rean schwarzer fei claussell alisa reinford eliot craig laura arseid jusis albarea machias regnitz sara valestin emma millstein gaius worzel 2 4 9 6 5 7 1 3 8 10
YES
In example 1 and 2, we have 3 people: tourist, Petr and me (cgy4ever). You can see that whatever handle is chosen, I must be the first, then tourist and Petr must be the last.
In example 3, if Copernicus uses "copernicus" as his handle, everything will be alright.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,p[100100];
struct NME
{
char str1[60],str2[60];
}name[100100];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s%s",name[i].str1,name[i].str2);
//cout<<name[i].str1<<" ... "<<name[i].str2<<endl;
}
for(int i=1;i<=n;i++) scanf("%d",p+i);
int pos=-1,se=-1;
bool flag=true;
if(strcmp(name[p[1]].str1,name[p[1]].str2)<0) pos=p[1],se=1;
else pos=p[1],se=2;
for(int i=2;i<=n&&flag;i++)
{
int id=p[i];
if(se==1)
{
bool ok1=false,ok2=false;
if(strcmp(name[pos].str1,name[id].str1)<0)
{
ok1=true;
}
if(strcmp(name[pos].str1,name[id].str2)<0)
{
ok2=true;
}
if(ok1&&ok2)
{
if(strcmp(name[id].str1,name[id].str2)<=0)
{
pos=id; se=1;
}
else if(strcmp(name[id].str2,name[id].str1)<0)
{
pos=id; se=2;
}
}
else if(ok1==true&&ok2==false)
{
pos=id; se=1;
}
else if(ok1==false&&ok2==true)
{
pos=id; se=2;
}
else
{
flag=false;
break;
}
}
else if(se==2)
{
bool ok1=false,ok2=false;
if(strcmp(name[pos].str2,name[id].str1)<0)
{
ok1=true;
}
if(strcmp(name[pos].str2,name[id].str2)<0)
{
ok2=true;
}
if(ok1&&ok2)
{
if(strcmp(name[id].str1,name[id].str2)<=0)
{
pos=id; se=1;
}
else if(strcmp(name[id].str2,name[id].str1)<0)
{
pos=id; se=2;
}
}
else if(ok1==true&&ok2==false)
{
pos=id; se=1;
}
else if(ok1==false&&ok2==true)
{
pos=id; se=2;
}
else
{
flag=false;
break;
}
}
}
if(flag==true) puts("YES");
else puts("NO");
return 0;
}There is an easy way to obtain a new task from an old one called "Inverse the problem": we give an output of the original task, and ask to generate an input, such that solution to the original problem will produce the output we provided. The hard task of Topcoder Open 2014 Round 2C, InverseRMQ, is a good example.
Now let's create a task this way. We will use the task: you are given a tree, please calculate the distance between any pair of its nodes. Yes, it is very easy, but the inverse version is a bit harder: you are given an n × n distance matrix. Determine if it is the distance matrix of a weighted tree (all weights must be positive integers).
The first line contains an integer n (1 ≤ n ≤ 2000) — the number of nodes in that graph.
Then next n lines each contains n integers di, j (0 ≤ di, j ≤ 109) — the distance between node i and node j.
If there exists such a tree, output "YES", otherwise output "NO".
3 0 2 7 2 0 9 7 9 0
YES
3 1 2 7 2 0 9 7 9 0
NO
3 0 2 2 7 0 9 7 9 0
NO
3 0 1 1 1 0 1 1 1 0
NO
2 0 0 0 0
NO
In the first example, the required tree exists. It has one edge between nodes 1 and 2 with weight 2, another edge between nodes 1 and 3 with weight 7.
In the second example, it is impossible because d1, 1 should be 0, but it is 1.
In the third example, it is impossible because d1, 2 should equal d2, 1.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long int LL;
const int maxn=2222;
int n;
LL d[maxn][maxn];
int main()
{
scanf("%d",&n);
bool flag=true;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%I64d",&d[i][j]);
if(i==j&&d[i][j]) flag=false;
}
}
for(int i=1;i<=n&&flag;i++)
for(int j=1;j<=n&&flag;j++)
{
if(d[i][j]!=d[j][i]) flag=false;
if(i!=j&&d[i][j]==0) flag=false;
}
if(flag==false)
{
puts("NO");
return 0;
}
for(int i=1;i<=n&&flag;i++)
{
LL MINI=(1LL<<62),pos=-1;
for(int j=1;j<=n;j++)
{
if(d[i][j]<MINI&&i!=j)
{
MINI=d[i][j]; pos=j;
}
}
for(int j=1;j<=n&&flag;j++)
{
if(j==i||j==pos) continue;
if(abs(d[pos][j]-d[i][j])!=d[i][pos])
{
flag=false;
}
}
}
if(flag==false)
{
puts("NO");
}
else
{
puts("YES");
}
return 0;
}
版权声明:来自: 代码代码猿猿AC路 http://blog.csdn.net/ck_boss




