一个Sqrt谋杀触发功能

我们*时常常会有一些数据运算的操作，须要调用sqrt，exp，abs等函数，那么时候你有没有想过：这个些函数系统是怎样实现的？就拿最常常使用的sqrt函数来说吧。系统怎么来实现这个常常调用的函数呢？

尽管有可能你*时没有想过这个问题，只是正所谓是“临阵磨枪，不快也光”，你“眉头一皱，计上心来”，这个不是太简单了嘛，用二分的方法。在一个区间中。每次拿中间数的*方来试验，假设大了，就再试左区间的中间数；假设小了。就再拿右区间的中间数来试。比方求sqrt(16)的结果，你先试（0+16）/2=8，8*8=64，64比16大。然后就向左移。试（0+8）/2=4。4*4=16刚好，你得到了正确的结果sqrt(16)=4。

然后你三下五除二就把程序写出来了：

float SqrtByBisection(float n) //用二分法 
{ 
	if(n<0) //小于0的依照你须要的处理 
		return n; 
	float mid,last; 
	float low,up; 
	low=0,up=n; 
	mid=(low+up)/2; 
	do
	{
		if(mid*mid>n)
			up=mid; 
		else 
			low=mid;
		last=mid;
		mid=(up+low)/2; 
	}while(abs(mid-last) > eps);//精度控制
	return mid; 
} 

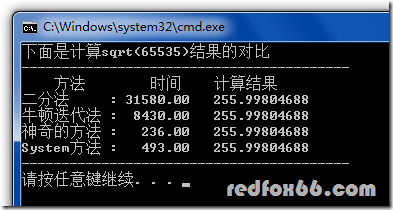
然后看看和系统函数性能和精度的区别（当中时间单位不是秒也不是毫秒。而是CPU Tick，无论单位是什么，统一了就有可比性） 

从图中能够看出，二分法和系统的方法结果上全然同样，可是性能上整整差了几百倍。为什么会有这么大的差别呢？难道系统有什么更好的办法？难道。。

。

。

哦，对了。回顾下我们以前的高数课，以前老师教过我们“牛顿迭代法高速寻找*方根”，或者这样的方法能够帮助我们。详细过程例如以下：

求出根号a的*似值：首先随便猜一个*似值x。然后不断令x等于x和a/x的*均数。迭代个六七次后x的值就已经相当精确了。 
比如。我想求根号2等于多少。假如我推測的结果为4。尽管错的离谱，但你能够看到使用牛顿迭代法后这个值非常快就趋*于根号2了： 
(       4  + 2/4        ) / 2 = 2.25 
(     2.25 + 2/2.25     ) / 2 = 1.56944.. 
( 1.56944..+ 2/1.56944..) / 2 = 1.42189.. 
( 1.42189..+ 2/1.42189..) / 2 = 1.41423.. 
....
这样的算法的原理非常easy，我们不过不断用(x,f(x))的切线来逼*方程x^2-a=0的根。

根号a实际上就是x^2-a=0的一个正实根，这个函数的导数是2x。

也就是说。函数上任一点(x,f(x))处的切线斜率是2x。那么，x-f(x)/(2x)就是一个比x更接*的*似值。代入 f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。

相关的代码例如以下：

float SqrtByNewton(float x)
{
	float val = x;//终于
	float last;//保存上一个计算的值
	do
	{
		last = val;
		val =(val + x/val) / 2;
	}while(abs(val-last) > eps);
	return val;
}

然后我们再来看下性能測试：

哇塞。性能提高了非常多，但是和系统函数相比，还是有这么大差距。这是为什么呀？想啊想啊。想了非常久仍然百思不得其解。突然有一天，我在网上看到一个奇妙的方法。于是就有了今天的这篇文章。废话不多说。看代码先：

float InvSqrt(float x)
{
	float xhalf = 0.5f*x;
	int i = *(int*)&x; // get bits for floating VALUE 
	i = 0x5f375a86- (i>>1); // gives initial guess y0
	x = *(float*)&i; // convert bits BACK to float
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

	return 1/x;
}

然后我们最后一次来看下性能測试：

这次真的是质变了。结果居然比系统的还要好。

。。

哥真的是震惊了！

。！

哥吐血了！。！一个函数引发了血案。！。血案，血案。。。

到如今你是不是还不明确那个“鬼函数”。究竟为什么速度那么快吗？不急，先看看以下的故事吧：

Quake-III Arena (雷神之锤3)是90年代的经典游戏之中的一个。该系列的游戏不但画面和内容不错，并且即使计算机配置低，也能极其流畅地执行。这要归功于它3D引擎的开发人员约翰-卡马克（John Carmack）。

其实早在90年代初DOS时代，仅仅要能在PC上搞个小动画都能让人惊叹一番的时候。John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励，doom, doomII,Quake...每次都把3-D技术推到极致。他的3D引擎代码资极度高效，差点儿是在压榨PC机的每条运算指令。当初MS的Direct3D也得听取他的意见，改动了不少API。

*期，QUAKE的开发商ID SOFTWARE 遵守GPL协议，公开了QUAKE-III的原代码，让世人有幸目睹Carmack传奇的3D引擎的原码。这是QUAKE-III原代码的下载地址： 
http://www.fileshack.com/file.x?

fid=7547

(以下是官方的下载网址，搜索 “quake3-1.32b-source.zip” 能够找到一大堆中文网页的。ftp://ftp.idsoftware.com/idstuff/source/quake3-1.32b-source.zip)

我们知道，越底层的函数。调用越频繁。3D引擎归根究竟还是数学运算。那么找到最底层的数学运算函数（在game/code/q_math.c），必定是精心编写的。

里面有非常多有趣的函数，非常多都令人惊奇。预计我们几年时间都学不完。在game/code/q_math.c里发现了这样一段代码。

它的作用是将一个数开*方并取倒，经測试这段代码比(float)(1.0/sqrt(x))快4倍：

float Q_rsqrt( float number )

{

        longi;

        floatx2, y;

        constfloat threehalfs = 1.5F;

 

        x2= number * 0.5F;

        y   = number;

        i   = * ( long * ) &y;   // evil floating point bit level hacking

        i   = 0x5f3759df - ( i >> 1 ); // what thefuck?

        y   = * ( float * ) &i;

        y   = y * ( threehalfs - ( x2 * y * y ) ); //1st iteration

        //y   = y * ( threehalfs - ( x2 * y * y )); // 2nd iteration, this can be removed

 

        returny;

} 

函数返回1/sqrt(x)。这个函数在图像处理中比sqrt(x)更实用。 
注意到这个函数仅仅用了一次叠代！

（事实上就是根本没用叠代。直接运算）。编译。实验。这个函数不仅工作的非常好，并且比标准的sqrt()函数快4倍。要知道。编译器自带的函数。但是经过严格细致的汇编优化的啊！

 
这个简洁的函数，最核心。也是最让人费解的，就是标注了“what the fuck?”的一句 
      i = 0x5f3759df - ( i >> 1 );

再加上y  = y * ( threehalfs - ( x2 * y *y ) ); 
两句话就完毕了开方运算。并且注意到。核心那句是定点移位运算。速度极快！特别在非常多没有乘法指令的RISC结构CPU上，这样做是极其高效的。

 

算法的原理事实上不复杂,就是牛顿迭代法,用x-f(x)/f'(x)来不断的逼*f(x)=a的根。

没错，一般的求*方根都是这么循环迭代算的可是卡马克(quake3作者)真正牛B的地方是他选择了一个神奇的常数0x5f3759df 来计算那个推測值，就是我们加凝视的那一行，那一行算出的值很接*1/sqrt(n)。这样我们仅仅须要2次牛顿迭代就能够达到我们所须要的精度。

好吧假设这个还不算NB,接着看:

普渡大学的数学家Chris Lomont看了以后认为有趣，决定要研究一下卡马克弄出来的这个推測值有什么奥秘。Lomont也是个牛人，在精心研究之后从理论上也推导出一个最佳推測值，和卡马克的数字很接*, 0x5f37642f。卡马克真牛，他是外星人吗？

传奇并没有在这里结束。Lomont计算出结果以后很惬意，于是拿自己计算出的起始值和卡马克的神奇数字做比赛。看看谁的数字可以更快更精确的求得*方根。

结果是卡马克赢了... 谁也不知道卡马克是怎么找到这个数字的。

最后Lomont怒了，採用暴力方法一个数字一个数字试过来，最终找到一个比卡马克数字要好上那么一丁点的数字，尽管实际上这两个数字所产生的结果很*似，这个暴力得出的数字是0x5f375a86。

Lomont为此写下一篇论文。"Fast Inverse Square Root"。

论文下载地址： 
http://www.math.purdue.edu/~clomont/Math/Papers/2003/InvSqrt.pdf 
http://www.matrix67.com/data/InvSqrt.pdf

最后，给出最精简的1/sqrt()函数：

float InvSqrt(float x)

{

        floatxhalf = 0.5f*x;

        inti = *(int*)&x; // get bits for floating VALUE

        i= 0x5f375a86- (i>>1); // gives initial guess y0

        x= *(float*)&i; // convert bits BACK to float

        x= x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

        returnx;

}

 

前两天有一则新闻，大意是说 Ryszard Sommefeldt 非常久曾经看到这么样的一段code (可能出自 Quake III 的 source code)：

float InvSqrt (float x)

{

        floatxhalf = 0.5f*x;

        inti = *(int*)&x;

        i= 0x5f3759df - (i>>1);

        x= *(float*)&i;

        x= x*(1.5f - xhalf*x*x);

        returnx;

}
PS. 这个 function 之所以重要，是由于求开根号倒数这个动作在 3D 运算 (向量运算的部份) 里面经常会用到，假设你用最原始的 sqrt() 然后再倒数的话。速度比上面的这个版本号大概慢了四倍吧… XD 
源代码下载地址：http://diducoder.com/sotry-about-sqrt.html

 

 

 

 

问题出在我签入的来自卡马克的求*方根函数代码。

double InvSqrt(double number)
{
      __int64 i;
      double x2, y;
      const double threehalfs = 1.5F;
    
      x2 = number * 0.5F;
      y = number;
      i = *(__int64 *)&y;
      i = 0x5fe6ec85e7de30da - (i >> 1);
      y = *( double *)&i;
      y = y * (threehalfs - (x2 * y * y)); //1stiteration
      y = y * (threehalfs - (x2 * y * y)); //2nditeration, this can be removed
      return y;
}

红色部分代码在gcc开启-fstrict-aliasing选项后将得到错误的代码。因为使用了type-punned pointer将打破strict-aliasing规则。

因为-fstrict-aliasing选项在-O2, -O3, -Os等优化模式下都将开启（眼下dev不带优化。main带-O3所以该问题仅仅在main上出现）所以建议对linux编译中产生
warning:dereferencing type-punned pointer will break strict-aliasing rule
警告的情况作为编译失败。以便防止出现类似问题。
上述代码应当使用联合体重写为：

double InvSqrt(double number)
{
      double x2, y;
      const double threehalfs = 1.5F;
      union
      {
            double d;
            __int64 i;
      }d;
      x2 = number * 0.5F;
      y = number;
      d.d =  y;
      d.i = 0x5fe6ec85e7de30da - (d.i >> 1);
      y = d.d;
      y = y * (threehalfs - (x2 * y * y)); //1stiteration
      y = y * (threehalfs - (x2 * y * y)); //2nditeration, this can be removed
      return y;
}

这样就不会打破该规则。

 

 

 

*方根倒数速算法

*方根倒数速算法（英语：Fast Inverse Square Root，亦常以“FastInvSqrt()”或其使用的十六进制常数0x5f3759df代称）是用于高速计算（即的*方根的倒数，在此需取符合IEEE 754标准格式的32位浮点数）的一种算法。

此算法最早可能是于90年代前期由SGI所发明。后来则于1999年在《雷神之锤III竞技场》的源码中应用。但直到2002－2003年间才在Usenet一类的公共论坛上出现。这一算法的优势在于降低了求*方根倒数时浮点运算操作带来的巨大的运算耗费，而在计算机图形学领域，若要求取照明和投影的波动角度与反射效果，就常需计算*方根倒数。

此算法首先接收一个32位带符浮点数，然后将之作为一个32位整数看待，以将其向右进行一次逻辑移位的方式将之取半，并用十六进制“魔术数字”0x5f3759df减之，如此就可以得对输入的浮点数的*方根倒数的首次*似值。而后又一次将其作为浮点数，以牛顿法重复迭代。以求出更精确的*似值，直至求出符合准确度要求的*似值。

在计算浮点数的*方根倒数的同一精度的*似值时，此算法比直接使用浮点数除法要快四倍。

1介绍

*方根倒数速算法最早被觉得是由约翰·卡马克所发明。但后来的调查显示，该算法在这之前就于计算机图形学的硬件与软件领域有所应用，如SGI和3dfx就曾在产品中应用此算法。而就如今所知，此算法最早由Gary Tarolli在SGIIndigo的开发中使用。虽说在随后的相关研究中也提出了一些可能的来源。但至今为止仍未能确切知晓此常数的起源。

2算法的切入点

浮点数的*方根倒数经常使用于计算正规化矢量。^[1] 3D图形程序须要使用正规化矢量来实现光照和投影效果。因此每秒都需做上百万次*方根倒数运算，而在处理坐标转换与光源的专用硬件设备出现前。这些计算都由软件完毕，计算速度亦相当之慢；在1990年代这段代码开发出来之时，多数浮点数操作的速度更是远远滞后于整数操作。因而针对正规化矢量算法的优化就显得尤为重要。

以下陈述计算正规化矢量的原理：

要将一个矢量标准化，就必须计算其欧几里得范数以求得矢量长度。而这时就需对矢量的各分量的*方和求*方根；而当求取到其长度并以之除该矢量的每一个分量后。所得的新矢量就是与原矢量同向的单位矢量，若以公式表示：

·    可求得矢量v的欧几里得范数。此算法正类如对欧几里得空间的两点求取其欧几里得距离。

·    而求得的就是标准化的矢量，若以代表。则有，

可见标准化矢量时须要用到对矢量分量的*方根倒数计算。所以对*方根倒数计算算法的优化对计算正规化矢量也大有裨益。

为了加速图像处理单元计算，《雷神之锤III竞技场》使用了*方根倒数速算法，而后来採用现场可编程逻辑门阵列的顶点着色器也应用了此算法。^[2] 

3将浮点数转化为整数

要理解这段代码。首先需了解浮点数的存储格式。

一个浮点数以32个二进制位表示一个有理数，而这32位由其意义分为三段：首先首位为符号位，如若是0则为正数，反之为负数。接下来的8位表示经过偏移处理（这是为了使之能表示-127－128）后的指数。最后23位表示的则是有效数字中除最高位以外的其余数字。

将上述结构表示成公式即为，当中表示有效数字的尾数（此处，偏移量，而指数的值决定了有效数字（在Lomont和McEniry的论文中称为“尾数”（mantissa））代表的是小数还是整数。以上图为例。将描写叙述带入有），且，则可得其表示的浮点数为。

符号位
0	1	1	1	1	1	1	1	=	127
0	0	0	0	0	0	1	0	=	2
0	0	0	0	0	0	0	1	=	1
0	0	0	0	0	0	0	0	=	0
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	0	=	−2
1	0	0	0	0	0	0	1	=	−127
1	0	0	0	0	0	0	0	=	−128

8位二进制整数补码演示样例

如上所述。一个有符号正整数在二进制补码系统中的表示中首位为0，而后面的各位则用于表示其数值。将浮点数取别名存储为整数时。该整数的数值即为，当中E表示指数，M表示有效数字；若以上图为例，图中例子若作为浮点数看待有。，则易知其转化而得的整数型号数值为。

因为*方根倒数函数仅能处理正数，因此浮点数的符号位（即如上的Si）必为0，而这就保证了转换所得的有符号整数也必为正数。

以上转换就为后面的计算带来了可行性，之后的第一步操作（逻辑右移一位）即是使该数的长整形式被2所除。^[3] 

4历史与考究

id Software创始人约翰·卡马克

《雷神之锤III》的代码直到QuakeCon 2005才正式放出，但早在2002年（或2003年）时*方根倒数速算法的代码就已经出如今Usenet与其它论坛上了。最初人们推測是卡马克写下了这段代码，但他在询问邮件的回复中否定了这个观点，并推測可能是先前曾帮id Software优化雷神之锤的资深汇编程序猿Terje Mathisen写下了这段代码；而在Mathisen的邮件里他表示在1990年代初他仅仅曾作过类似的实现。确切来说这段代码亦非他所作。如今所知的最早实现是由Gary Tarilli在SGIIndigo中实现的，但他亦坦承他仅对常数R的取值做了一定的改进，实际上他也不是作者。

RysSommefeldt则在向以发明MATLAB而闻名的CleveMoler查证后觉得原始的算法是Ardent Computer公司的GregWalsh所发明，但他也没有不论什么决定性的证据能证明这一点。

眼下不仅该算法的原作者不明，人们也仍无法明白当初选择这个“魔术数字”的方法。Chris Lomont在研究中曾做了个试验：他编写了一个函数，以在一个范围内遍历选取R值的方式将逼*误差降到最小，以此方法他计算出了线性*似的最优R值0x5f37642f（与代码中使用的0x5f3759df相当接*）。但以之代入算法计算并进行一次牛顿迭代后，所得*似值与代入0x5f3759df的结果相比精度却仍稍微更低；而后Lomont将目标改为遍历选取在进行1－2次牛顿迭代后能得到最大精度的R值。并由此算出最优R值为0x5f375a86，以此值代入算法并进行牛顿迭代后所得的结果都比代入原始值（0x5f3759df）更精确，于是他的论文最后以“原始常数是以数学推导还是以重复试错的方式求得”的问题作结。

在论文中Lomont亦指出64位的IEEE754浮点数（即双精度类型）所相应的魔术数字是0x5fe6ec85e7de30da，但后来的研究表明代入0x5fe6eb50c7aa19f9的结果准确度更高（McEniry得出的结果则是0x5FE6EB50C7B537AA，精度介于两者之间）。

在Charles McEniry的论文中，他使用了一种类似Lomont但更复杂的方法来优化R值：他最開始使用穷举搜索法。所得结果与Lomont同样。而后他尝试用带权二分法寻找最优值。所得结果恰是代码中所使用的魔术数字0x5f3759df，因此McEniry确信这一常数也许最初便是以“在可容忍误差范围内使用二分法”的方式求得。^[4] 

5凝视

1. 因为现代计算机系统对长整型的定义有所差异，使用长整型会减少此段代码的可移植性。

详细来说。由此段浮点转换为长整型的定义可知，如若这段代码正常执行，所在系统的长整型长度应为4字节（32位），否则又一次转为浮点数时可能会变成负数；而因为C99标准的广泛应用，在现今多数64位计算机系统（除使用LLP64数据模型的Windows外）中。长整型的长度都是8字节。^[5] 

2. 此处“浮点数”所指为标准化浮点数，也即有效数字部分必须满足，可參见DavidGoldberg. What Every Computer Scientist Should Know About Floating-PointArithmetic. ACM Computing Surveys. 1991.March, 23 (1): 5–48. doi:10.1145/103162.103163.

3. Lomont 2003确定R的方式则有所不同，他先将R分解为与，当中与分别代表R的有效数字域和指数域。^[6] 

 

 

 

 

 

卡马克高速*方根---*方根倒数算法 [转]

--------------------------------------------------------------------------------
 高速*方根（*方根倒数）算法

日前在书上看到一段使用多项式逼*计算*方根的代码，至今都没搞明确作者是如何推算出那个公式的。

但在尝试解决这个问题的过程中，学到了不少东西，于是便有了这篇心得，写出来和大家共享。

当中有错漏的地方，还请大家多多不吝赐教。

的确，正如很多人所说的那样，如今有有FPU，有3DNow。有SIMD，讨论软件算法好像不合时宜。

关于sqrt的话题事实上早在2003年便已在 GameDev.net上得到了广泛的讨论（可见我实在很火星了，当然不排除还有其它尚在冥王星的人，嘿嘿）。而尝试探究该话题则全然是出于本人的兴趣和好奇心（换句话说就是无知）。

我仅仅是个beginner，所以这样的大是大非的问题我也说不清楚（在GameDev.net上也有非常多类似的争论）。

但不管怎样，Carmack在DOOM3中还是使用了软件算法。而多知道一点数学知识对3D编程来说也仅仅有优点没坏处。3D图形编程事实上就是数学，数学。还是数学。

=========================================================

在3D图形编程中，常常要求*方根或*方根的倒数，比如：求向量的长度或将向量归一化。C数学函数库中的sqrt具有理想的精度，但对于3D游戏程式来说速度太慢。我们希望可以在保证足够的精度的同一时候。进一步提快速度。

Carmack在QUAKE3中使用了以下的算法。它第一次在公众场合出现的时候，差点儿震住了全部的人。据说该算法事实上并非Carmack发明的，它真正的作者是Nvidia的GaryTarolli（未经证实）。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
//
// 计算參数x的*方根的倒数
//
float InvSqrt (float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x;
i = 0x5f3759df - (i >> 1); // 计算第一个*似根
x = *(float*)&i;
x = x*(1.5f - xhalf*x*x); // 牛顿迭代法
return x;
}
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
该算法的本质事实上就是牛顿迭代法（Newton-RaphsonMethod。简称NR）。而NR的基础则是泰勒级数（Taylor Series）。

NR是一种求方程的*似根的方法。首先要预计一个与方程的根比較靠*的数值。然后依据公式推算下一个更加*似的数值，不断反复直到能够获得惬意的精度。

其公式例如以下：
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
函数：y=f(x)
其一阶导数为：y'=f'(x)
则方程：f(x)=0 的第n+1个*似根为
x[n+1] = x[n] - f(x[n]) / f'(x[n])
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
 NR最关键的地方在于预计第一个*似根。

假设该*似根与真根足够靠*的话，那么仅仅须要少数几次迭代，就能够得到惬意的解。

如今回过头来看看怎样利用牛顿法来解决我们的问题。求*方根的倒数，实际就是求方程1/(x^2)-a=0的解。将该方程按牛顿迭代法的公式展开为：
x[n+1]=1/2*x[n]*(3-a*x[n]*x[n])
 将1/2放到括号中面，就得到了上面那个函数的倒数第二行。

接着，我们要设法预计第一个*似根。这也是上面的函数最奇妙的地方。

它通过某种方法算出了一个与真根很接*的*似根，因此它仅仅须要使用一次迭代过程就获得了较惬意的解。它是如何做到的呢？全部的奥妙就在于这一行：
i = 0x5f3759df - (i >> 1); // 计算第一个*似根

超级莫名其妙的语句。不是吗？但细致想一下的话。还是能够理解的。我们知道，IEEE标准下，float类型的数据在32位系统上是这样表示的（大体来说就是这样，但省略了非常多细节，有兴趣能够GOOGLE）：
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
bits：31 30... 0
31：符号位
30-23：共8位，保存指数（E）
22-0：共23位，保存尾数（M）
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
所以。32位的浮点数用十进制实数表示就是：M*2^E。开根然后倒数就是：M^(-1/2)*2^(-E/2)。如今就十分清晰了。语句i> >1其工作就是将指数除以2。实现2^(E/2)的部分。

而前面用一个常数减去它，目的就是得到M^(1/2)同一时候反转全部指数的符号。

至于那个0x5f3759df，呃，我仅仅能说，的确是一个超级的MagicNumber。

那个Magic Number是能够推导出来的，但我并不打算在这里讨论，由于实在太繁琐了。简单来说。其原理例如以下：由于IEEE的浮点数中，尾数M省略了最前面的1。所以实际的尾数是1+M。

假设你在大学上数学课没有打瞌睡的话，那么当你看到(1+M)^(-1/2)这种形式时。应该会立即联想的到它的泰勒级数展开，而该展开式的第一项就是常数。

以下给出简单的推导过程：
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
对于实数R>0，如果其在IEEE的浮点表示中，
指数为E，尾数为M，则：

R^(-1/2)
= (1+M)^(-1/2) * 2^(-E/2)

将(1+M)^(-1/2)按泰勒级数展开，取第一项，得：

原式
= (1-M/2) * 2^(-E/2)
= 2^(-E/2) - (M/2) * 2^(-E/2)

假设不考虑指数的符号的话。
(M/2)*2^(E/2)正是(R>>1)。
而在IEEE表示中。指数的符号仅仅需简单地加上一个偏移就可以，
而式子的前半部分刚好是个常数，所以原式能够转化为：

原式 = C - (M/2)*2^(E/2) = C -(R>>1)，当中C为常数

所以仅仅须要解方程：
R^(-1/2)
= (1+M)^(-1/2) * 2^(-E/2)
= C - (R>>1)
求出令到相对误差最小的C值就能够了
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
上面的推导过程仅仅是我个人的理解，并未得到证实。而ChrisLomont则在他的论文中具体讨论了最后那个方程的解法。并尝试在实际的机器上寻找最佳的常数C。有兴趣的朋友能够在文末找到他的论文的链接。

所以。所谓的Magic Number，并非从N元宇宙的某个星系因为时空扭曲而掉到地球上的，而是几百年前就有的数学理论。仅仅要熟悉NR和泰勒级数，你我相同有能力作出类似的优化。

在GameDev.net上有人做过測试，该函数的相对误差约为0.177585%，速度比C标准库的sqrt提高超过20%。假设添加一次迭代过程，相对误差能够减少到e-004 的级数。但速度也会降到和sqrt差点儿相同。

据说在DOOM3中。Carmack通过查找表进一步优化了该算法，精度*乎完美。并且速度也比原版提高了一截（正在努力弄源代码。谁有发我一份）。

值得注意的是。在Chris Lomont的演算中。理论上最棒的常数（精度最高）是0x5f37642f，而且在实际測试中，假设仅仅使用一次迭代的话，其效果也是最好的。但奇怪的是。经过两次NR后，在该常数下解的精度将减少得很厉害（天知道是怎么回事！

）。经过实际的測试，Chris Lomont觉得。最棒的常数是0x5f375a86。

假设换成64位的double版本号的话。算法还是一样的，而最优常数则为0x5fe6ec85e7de30da（又一个令人冒汗的Magic Number - -b）。

这个算法依赖于浮点数的内部表示和字节顺序。所以是不具移植性的。假设放到Mac上跑就会挂掉。

假设想具备可移植性。还是乖乖用sqrt好了。但算法思想是通用的。大家能够尝试推算一下对应的*方根算法。

以下给出Carmack在QUAKE3中使用的*方根算法。

Carmack已经将QUAKE3的全部源码捐给开源了。所以大家能够放心使用，不用操心会受到律师信。
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
//
// Carmack在QUAKE3中使用的计算*方根的函数
//
float CarmSqrt(float x){
union{
int intPart;
float floatPart;
} convertor;
union{
int intPart;
float floatPart;
} convertor2;
convertor.floatPart = x;
convertor2.floatPart = x;
convertor.intPart = 0x1FBCF800 + (convertor.intPart >> 1);
convertor2.intPart = 0x5f3759df - (convertor2.intPart >> 1);
return 0.5f*(convertor.floatPart + (x * convertor2.floatPart));
}

 

 

 

日前在书上看到一段使用多项式逼*计算*方根的代码，至今都没搞明确作者是如何推算出那个公式的。

但在尝试解决这个问题的过程中，学到了不少东西，于是便有了这篇心得，写出来和大家共享。

当中有错漏的地方，还请大家多多不吝赐教。 

的确，正如很多人所说的那样，如今有有FPU，有3DNow。有SIMD，讨论软件算法好像不合时宜。关于sqrt的话题事实上早在2003年便已在 GameDev.net上得到了广泛的讨论（可见我实在很火星了，当然不排除还有其它尚在冥王星的人。嘿嘿）。而尝试探究该话题则全然是出于本人的兴趣和好奇心（换句话说就是无知）。 

我仅仅是个beginner，所以这样的大是大非的问题我也说不清楚（在GameDev.net上也有非常多类似的争论）。

但不管怎样。Carmack在DOOM3中还是使用了软件算法，而多知道一点数学知识对3D编程来说也仅仅有优点没坏处。3D图形编程事实上就是数学，数学，还是数学。 

========================================================= 

在3D图形编程中，常常要求*方根或*方根的倒数。比如：求向量的长度或将向量归一化。

C数学函数库中的sqrt具有理想的精度。但对于3D游戏程式来说速度太慢。

我们希望可以在保证足够的精度的同一时候，进一步提快速度。 

Carmack在QUAKE3中使用了以下的算法。它第一次在公众场合出现的时候，差点儿震住了全部的人。据说该算法事实上并非Carmack发明的，它真正的作者是Nvidia的Gary Tarolli（未经证实）。 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
// 
// 计算參数x的*方根的倒数 
// 
float InvSqrt (float x) 
{ 
float xhalf = 0.5f*x; 
int i = *(int*)&x; 
i = 0x5f3759df - (i >> 1); // 计算第一个*似根 
x = *(float*)&i; 
x = x*(1.5f - xhalf*x*x); // 牛顿迭代法 
return x; 
} 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
该算法的本质事实上就是牛顿迭代法（Newton-Raphson Method，简称NR）。而NR的基础则是泰勒级数（TaylorSeries）。NR是一种求方程的*似根的方法。

首先要预计一个与方程的根比較靠*的数值，然后依据公式推算下一个更加*似的数值。不断反复直到能够获得惬意的精度。

其公式例如以下： 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
函数：y=f(x) 
其一阶导数为：y'=f'(x) 
则方程：f(x)=0 的第n+1个*似根为 
x[n+1] = x[n] - f(x[n]) / f'(x[n]) 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
NR最关键的地方在于预计第一个*似根。假设该*似根与真根足够靠*的话，那么仅仅须要少数几次迭代，就能够得到惬意的解。 

如今回过头来看看怎样利用牛顿法来解决我们的问题。求*方根的倒数，实际就是求方程1/(x^2)-a=0的解。将该方程按牛顿迭代法的公式展开为： 
x[n+1]=1/2*x[n]*(3-a*x[n]*x[n]) 
将1/2放到括号中面，就得到了上面那个函数的倒数第二行。

 

接着。我们要设法预计第一个*似根。

这也是上面的函数最奇妙的地方。它通过某种方法算出了一个与真根很接*的*似根。因此它仅仅须要使用一次迭代过程就获得了较惬意的解。

它是如何做到的呢？全部的奥妙就在于这一行： 
i = 0x5f3759df - (i >> 1); // 计算第一个*似根 

超级莫名其妙的语句。不是吗？但细致想一下的话，还是能够理解的。我们知道。IEEE标准下，float类型的数据在32位系统上是这样表示的（大体来说就是这样，但省略了非常多细节。有兴趣能够GOOGLE）： 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
bits：3130 ... 0 
31：符号位 
30-23：共8位。保存指数（E） 
22-0：共23位。保存尾数（M） 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
所以。32位的浮点数用十进制实数表示就是：M*2^E。开根然后倒数就是：M^(-1/2)*2^(-E/2)。如今就十分清晰了。

语句i> >1其工作就是将指数除以2。实现2^(E/2)的部分。而前面用一个常数减去它，目的就是得到M^(1/2)同一时候反转全部指数的符号。 

至于那个0x5f3759df。呃，我仅仅能说，的确是一个超级的Magic Number。 

那个MagicNumber是能够推导出来的。但我并不打算在这里讨论，由于实在太繁琐了。简单来说，其原理例如以下：由于IEEE的浮点数中。尾数M省略了最前面的1。所以实际的尾数是1+M。假设你在大学上数学课没有打瞌睡的话，那么当你看到(1+M)^(-1/2)这种形式时，应该会立即联想的到它的泰勒级数展开，而该展开式的第一项就是常数。以下给出简单的推导过程： 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
对于实数R>0。如果其在IEEE的浮点表示中。 
指数为E，尾数为M。则： 

R^(-1/2) 
= (1+M)^(-1/2) * 2^(-E/2) 

将(1+M)^(-1/2)按泰勒级数展开，取第一项，得： 

原式 
= (1-M/2) * 2^(-E/2) 
= 2^(-E/2) - (M/2) * 2^(-E/2) 

假设不考虑指数的符号的话， 
(M/2)*2^(E/2)正是(R>>1)， 
而在IEEE表示中。指数的符号仅仅需简单地加上一个偏移就可以。 
而式子的前半部分刚好是个常数，所以原式能够转化为： 

原式= C - (M/2)*2^(E/2) = C - (R>>1)，当中C为常数 

所以仅仅须要解方程： 
R^(-1/2) 
= (1+M)^(-1/2) * 2^(-E/2) 
= C - (R>>1) 
求出令到相对误差最小的C值就能够了 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
上面的推导过程仅仅是我个人的理解，并未得到证实。而Chris Lomont则在他的论文中具体讨论了最后那个方程的解法，并尝试在实际的机器上寻找最佳的常数C。有兴趣的朋友能够在文末找到他的论文的链接。

 

所以，所谓的Magic Number，并非从N元宇宙的某个星系因为时空扭曲而掉到地球上的。而是几百年前就有的数学理论。

仅仅要熟悉NR和泰勒级数，你我相同有能力作出类似的优化。

 

在GameDev.net上有人做过測试，该函数的相对误差约为0.177585%。速度比C标准库的sqrt提高超过20%。

假设添加一次迭代过程，相对误差能够减少到e-004 的级数。但速度也会降到和sqrt差点儿相同。据说在DOOM3中。Carmack通过查找表进一步优化了该算法。精度*乎完美，并且速度也比原版提高了一截（正在努力弄源代码，谁有发我一份）。 

值得注意的是，在Chris Lomont的演算中，理论上最棒的常数（精度最高）是0x5f37642f，而且在实际測试中，假设仅仅使用一次迭代的话，其效果也是最好的。

但奇怪的是，经过两次NR后，在该常数下解的精度将减少得很厉害（天知道是怎么回事！）。经过实际的測试，Chris Lomont觉得。最棒的常数是0x5f375a86。假设换成64位的double版本号的话，算法还是一样的。而最优常数则为0x5fe6ec85e7de30da（又一个令人冒汗的Magic Number - -b）。 

这个算法依赖于浮点数的内部表示和字节顺序。所以是不具移植性的。假设放到Mac上跑就会挂掉。假设想具备可移植性，还是乖乖用sqrt好了。

但算法思想是通用的。大家能够尝试推算一下对应的*方根算法。 

以下给出Carmack在QUAKE3中使用的*方根算法。

Carmack已经将QUAKE3的全部源码捐给开源了，所以大家能够放心使用。不用操心会受到律师信。

 
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ 
// 
// Carmack在QUAKE3中使用的计算*方根的函数 
// 
float CarmSqrt(float x){ 
union{ 
int intPart; 
float floatPart; 
} convertor; 
union{ 
int intPart; 
float floatPart; 
} convertor2; 
convertor.floatPart = x; 
convertor2.floatPart = x; 
convertor.intPart = 0x1FBCF800 + (convertor.intPart >> 1); 
convertor2.intPart = 0x5f3759df - (convertor2.intPart >> 1); 
return 0.5f*(convertor.floatPart + (x * convertor2.floatPart)); 
} 

 

 

 

 

1.     #include <iostream> #include <math.h>

2.     using namespace std;

3.     

4.     float InvSqrt (float x)

5.     {

6.             float xhalf = 0.5f*x;

7.             int i = *(int*)&x;

8.             i = 0x5f3759df - (i >> 1); // 计算第一个*似根

9.             x = *(float*)&i;

10.           x = x*(1.5f - xhalf*x*x); // 牛顿迭代法

11.           return x;

12.   }

13.   

14.   float CarmSqrt(float x){

15.           union{

16.                   int intPart;

17.                   float floatPart;

18.           } convertor;

19.           union{

20.                   int intPart;

21.                   float floatPart;

22.           } convertor2;

23.           convertor.floatPart = x;

24.           convertor2.floatPart = x;

25.           convertor.intPart = 0x1FBCF800 + (convertor.intPart >> 1);

26.           convertor2.intPart = 0x5f3759df - (convertor2.intPart >> 1);

27.           return 0.5f*(convertor.floatPart + (x * convertor2.floatPart));

28.   }

29.   

30.   int main()

31.   {

32.           float a = 0.25;

33.   

34.           cout << InvSqrt(a) << endl;

35.           cout << CarmSqrt(a) << endl;

36.           cout << sqrt(a) << endl;

37.   

38.           return 0;

39.   }

结果例如以下：

普通浏览复制代码

1.  1.99661     

2.  0.488594

3.  0.5

4.  请按随意键继续. . .

代码没错，仅仅是cout << InvSqrt(a) << endl;应该改成cout <<1.0f / InvSqrt(a) << endl;。所以我提到了就这个样例来说，精度已经非常不错了。

 

 

 

 

主要思想利用了浮点数的表示法，ieee的标准当中关键部分是

int i = *(int*)&x; 
i = 0x5f3759df - (i >> 1); // 计算第一个*似根 
x = *(float*)&i; 
对于0x5f3759df假设看成浮点数的话，其指数位为(0101)(1111)0->1011111=190

设原来的xIEEE表示的指数位为a。则新的结果的指数位变成了190-a/2

假设要转换成 m*2^n格式，须要将指数a-127。所以得到的新结果用数学表示的指数位为

190-a/2-127= 63-a/2 

而x的原来假设从ieee格式变成数学表示应为a-127。比較63-a/2与a-127。能够看出指数之间的关系为

63-a/2==（a-127)*(-1/2)。

x应该已经是1/sqrt(x)的*似值

 

 

 

首先看牛顿迭代法的原理

 

若函数

f（x）在点的某一临域内具有直到（n+1）阶导数，则在该邻域内f（x）的n阶泰勒公式为：

f(x) = f(x0)+(x－x0)f'(x0)+(x－x0)^2*f''(x0)/2! +… +...fn(x0)(x- x0)n/n!....

解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种*似方法。把f(x)在x0点附*展开成泰勒级数 f(x) = f(x0)+(x－x0)f'(x0)+(x－x0)^2*f''(x0)/2! +…

 

取其线性部分。作为非线性方程f(x) = 0的*似方程，即泰勒展开的前两项，则有

f(x0)+f'(x0)(x－x0)=f(x)=0 

设f'(x0)≠0则f(x0)+f'(x0)(x－x0)=0 

其解为x1=x0－f(x0)/f'(x0) 

这样，得到牛顿法的一个迭代序列：x(n+1)=x(n)－f(x(n))/f'(x(n))。

也就是说x(n+1)=x(n)－f(x(n))/f'(x(n))。是用来计算f(x)=0的根的迭代公式，

假设x(n)与真根足够靠*的话，那么仅仅须要少数几次迭代，就能够得到惬意的解。

 

我们如今要求的是一个数的*方根的倒数，设这个数为a，那么我们要计算的就是x= a^(-0.5)

。首先我们要把这个计算需求转换为f(x)=0的形式。

 

x = a^(-0.5) 

x^(-2) = a 

x^(-2)-a = 0 

这样就转化成了f(x) = 0的形式。当中x就是a的*方根的倒数。

 

f(x) = x^(-2)-a 则f'(x) = -2*x^(-3) 依据牛顿迭代公式能够得到

 

x(n+1) = x(n) - (x(n)^(-2) - a)/(-2*x(n)^(-3)) 

x(n+1) = x(n) + (x(n)^(-2) - a)/(2*x(n)^(-3)) 

x(n+1) = x(n) + (x(n)/2) - (a*x(n)^3)/2 

x(n+1) = 1.5*x(n) - (0.5*a*x(n)^3) 

这样我们就得到了迭代计算的公式。也就是源程序中的

 x=x*(1.5f-xhalf*x*x); 

 

以下关键的一步就是计算x(n)的一个真根足够靠*的*似值。

主要思想利用了浮点数的表示法，

ieee754标准当中关键部分是

 long i=*(long*)&x; 

 i=0x5f3759df - (i>>1); 

x=*(float *)&i; 

其它地方都比較简单，这三句的意思，应当是把x的浮点表示格式直接看出long类型的，

然后进行0x5f3759df - (i>>1)运算。之后再直接把long类型的看成float类型的。当中的数学道理，我大致看了下

对于浮点数的表示，在ieee里float类型是依照符号指数.尾数格式进行的。当中符号位1位，指数位8位，尾数23位。先仅仅考虑指数部分。

 

long i=*(long*)&x;是把浮点数看成了与他具有同样位格式的long型数。

i=0x5f3759df - (i>>1);

对于0x5f3759df,假设看成浮点数的话，二进制位为

.10111110.01101110101100111011111,

其指数位为10111110=190 。

 

设原来的x的IEEE表示的指数位为a则新的结果的指数位变成了190-a/2；注意假设要转换成

m*2^n格式，须要将指数减去127；所以得到的新结果用数学表示的指数位为190-a/2-127= 63-a/2 。而x的原来的指数a，假设从ieee格式变成数学表示应为a-127 。

 

比較63-a/2与a-127，能够看出指数之间的关系为63-a/2==（a-127)*(-1/2) 

所以经过上述三句。x应该已经是1/sqrt(x)的*似值。

当然上面仅仅是从指数位进行了简单分析，假设要细化到尾数，还须要看详细效果。

 

 

 

 

在3D图形编程中，常常要求*方根或*方根的倒数。比如：求向量的长度或将向量归一化。C数学函数库中的sqrt具有理想的精度，但对于3D游戏程式来说速度太慢。我们希望可以在保证足够的精度的同一时候。进一步提快速度。

Carmack在QUAKE3中使用了以下的算法，它第一次在公众场合出现的时候，差点儿震住了全部的人。

据说该算法事实上并非Carmack发明的，它真正的作者是Nvidia的Gary Tarolli（未经证实）。

 

//
// 计算參数x的*方根的倒数
//
float InvSqrt (float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x;
i = 0x5f3759df - (i >> 1); // 计算第一个*似根
x = *(float*)&i;
x = x*(1.5f - xhalf*x*x); // 牛顿迭代法
return x;
}

该算法的本质事实上就是牛顿迭代法（Newton-RaphsonMethod，简称NR）。而NR的基础则是泰勒级数（Taylor Series）。

NR是一种求方程的*似根的方法。首先要预计一个与方程的根比較靠*的数值，然后依据公式推算下一个更加*似的数值，不断反复直到能够获 得惬意的精度。其公式例如以下：

函数：y=f(x),其一阶导数为：y'=f'(x)

则方程：f(x)=0 的第n+1个*似根为

x[n+1] = x[n] - f(x[n]) / f'(x[n])NR最关键的地方在于预计第一个*似根。假设该*似根与真根足够靠*的话，那么仅仅须要少数几次迭代，就能够得到惬意的解。

如今回过头来看看怎样利用牛顿法来解决我们的问题。求*方根的倒数。实际就是求方程1/(x^2)-a=0的解。将该方程按牛顿迭代法的公式展开为：

x[n+1]=1/2*x[n]*(3-a*x[n]*x[n])将1/2放到括号中面，就得到了上面那个函数的倒数第二行。

接着，我们要设法预计第一个*似根。这也是上面的函数最奇妙的地方。

它通过某种方法算出了一个与真根很接*的*似根，因此它仅仅须要使用一次迭代过程就获得了较惬意的解。它是如何做到的呢？全部的奥妙就在于这一行：

i = 0x5f3759df - (i >> 1); // 计算第一个*似根超级莫名其妙的语句。不是吗？但细致想一下的话，还是能够理解的。

我们知道。IEEE标准下，float类型的数据在32位系统上是这样 表示的（大体来说就是这样，但省略了非常多细节，有兴趣能够GOOGLE）：

bits：31 30 ... 0
31：符号位
30-23：共8位，保存指数（E）
22-0：共23位，保存尾数（M）所 以，32位的浮点数用十进制实数表示就是：M*2^E。开根然后倒数就是：M^(-1/2)*2^(-E/2)。

如今就十分清晰了。

语句 i>>1其工作就是将指数除以2，实现2^(E/2)的部分。而前面用一个常数减去它，目的就是得到M^(1/2)同一时候反转全部指数的符号。

至于那个0x5f3759df。呃，我仅仅能说。的确是一个超级的Magic Number。

那个Magic Number是能够推导出来的，但我并不打算在这里讨论，由于实在太繁琐了。简单来说。其原理例如以下：由于IEEE的浮点数中。尾数M省略了最前面的1，所 以实际的尾数是1+M。假设你在大学上数学课没有打瞌睡的话。那么当你看到(1+M)^(-1/2)这种形式时，应该会立即联想的到它的泰勒级数展开。 而该展开式的第一项就是常数。以下给出简单的推导过程：

对于实数R>0。如果其在IEEE的浮点表示中。
指数为E，尾数为M，则：R^(-1/2) = (1+M)^(-1/2) * 2^(-E/2)

 将(1+M)^(-1/2)按泰勒级数展开，取第一项。得：

原式= (1-M/2) * 2^(-E/2)=2^(-E/2) - (M/2) * 2^(-E/2)

假设不考虑指数的符号的话。
(M/2)*2^(E/2)正是(R>>1)。
而在IEEE表示中，指数的符号仅仅需简单地加上一个偏移就可以，而式子的前半部分刚好是个常数，所以原式能够转化为：

原式 = C - (M/2)*2^(E/2) = C- (R>>1)，当中C为常数

所以仅仅须要解方程：
R^(-1/2)
= (1+M)^(-1/2) * 2^(-E/2)
= C - (R>>1)
求出令到相对误差最小的C值就能够了上面的推导过程仅仅是我个人的理解，并未得到证实。

而Chris Lomont则在他的论文中具体讨论了最后那个方程的解法。并尝试在实际的机器上寻找最佳的常数C。有兴趣的朋友能够在文末找到他的论文的链接。

所以，所谓的Magic Number，并非从N元宇宙的某个星系因为时空扭曲而掉到地球上的，而是几百年前就有的数学理论。

仅仅要熟悉NR和泰勒级数。你我相同有能力作出类似的优化。

在http://GameDev.net上有人做过測试，该函数的相对误差约为0.177585%，速度比C标准库的sqrt提高超过20%。

假设添加一次迭代过 程，相对误差能够减少到e-004的级数，但速度也会降到和sqrt差点儿相同。

据说在DOOM3中，Carmack通过查找表进一步优化了该算法。精度*乎完美。并且速度也比原版提高了一截（正在努力弄源代码。谁有发我一份）。

值得注意的是，在Chris Lomont的演算中，理论上最棒的常数（精度最高）是0x5f37642f。而且在实际測试中，假设仅仅使用一次迭代的话，其效果也是最好的。

但奇怪的 是。经过两次NR后。在该常数下解的精度将减少得很厉害（天知道是怎么回事！）。经过实际的測试，Chris Lomont觉得，最棒的常数是0x5f375a86。

假设换成64位的double版本号的话，算法还是一样的。而最优常数则为 0x5fe6ec85e7de30da（又一个令人冒汗的Magic Number- -b）。

这个算法依赖于浮点数的内部表示和字节顺序。所以是不具移植性的。假设放到Mac上跑就会挂掉。

假设想具备可移植性，还是乖乖用sqrt好了。但算法思想是通用的。大家庭可以尝试对相应的*方根算法预测。

 

版权声明：本文【借给你1秒】原创文章，转载请注明出处。