LSH算法原理
原文链接--http://www.jiahenglu.net/NSFC/LSH.html
LSH(Location Sensitive Hash),即位置敏感哈希函数。
与一般哈希函数不同的是位置敏感性,也就是散列前的类似点经过哈希之后,也可以在一定程度上类似,而且具有一定的概率保证。
形式化定义:
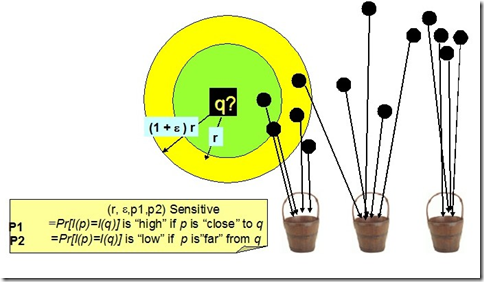
对于随意q,p属于S,若从集合S到U的函数族H={h1,h2...hn}对距离函数D(,),如欧式距离、曼哈顿距离等等,满足条件:
则称D(,)是位置敏感的。
例如以下图。空间上的点经位置敏感哈希函数散列之后,对于q,其rNN有可能散列到同一个桶(如第一个桶),即散列到第一个桶的概率较大。会大于某一个概率阈值p1;而其(1+emxilong)rNN之外的对象则不太可能散列到第一个桶。即散列到第一个桶的概率非常小,会小于某个阈值p2.
LSH的作用
◆高维下近似查询
类似性检索在各种领域特别是在视频、音频、图像、文本等含有丰富特征信息领域中的应用变得越来越重要。丰富的特征信息一般用高维向量表示,由此类似性检索一般通过K近邻或近似近邻查询来实现。
一个理想的类似性检索一般须要满足下面四个条件:
1. 高准确性。
即返回的结果和线性查找的结果接近。
2. 空间复杂度低。即占用内存空间少。理想状态下,空间复杂度随数据集呈线性增长,但不会远大于数据集的大小。
3. 时间复杂度低。检索的时间复杂度最好为O(1)或O(logN)。
4. 支持高维度。可以较灵活地支持高维数据的检索。
传统主要方法是基于空间划分的算法——tree相似算法。如R-tree。Kd-tree,SR-tree。这样的算法返回的结果是精确的。可是这样的算法在高维数据集上的时间效率并不高。实验[1]指出维度高于10之后,基于空间划分的算法时间复杂度反而不如线性查找。LSH方法可以在保证一定程度上的准确性的前提下,时间和空间复杂度得到减少,而且可以非常好地支持高维数据的检索。
◆分类和聚类
依据LSH的特性,就可以将相近(类似)的对象散列到同一个桶之中,则能够对图像、音视频、文本等丰富的高维数据进行分类或聚类。
◆数据压缩。如广泛地应用于信号处理及数据压缩等领域的Vector Quantization量子化技术。
总而言之,哪儿须要近似kNN查询,哪儿都能用上LSH.
[1] Weber R, Schek H, Blott S. A quantitative analysis and performance study for similarity search methods in high dimensional spaces Proc.of the 24th Intl.Conf.on Very Large Data Bases (VLDB).1998:194-205