LBP特征 学习笔记

这几天一直在做人脸识别的项目，有用到LBP特征，但是毫无头绪，师姐这几天也比较忙，没有时间来指导我，随自己找相应的介绍LBP的博文来看，现在总算有了一个大体的思路了，就写下来吧

注：参考博文： 目标检测的图像特征提取之（二）LBP特征       也谈LBP

LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征；

 

1、LBP特征的描述

       原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

 

LBP的改进版本：

       原始的LBP提出后，研究人员不断对其提出了各种改进和优化。

（1）圆形LBP算子：

        基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala 等对 LBP 算子进行了改进，将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子；

（2）LBP旋转不变模式

       从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。

       后来就有人提出了旋转不变模式的LBP特征值，他们认为下图的8个LBP是等价的，也就是说LBP有了旋转不变性，也就是说，图中的 8 种 LBP 模式对应的旋转不变的 LBP 模式都是00001111。

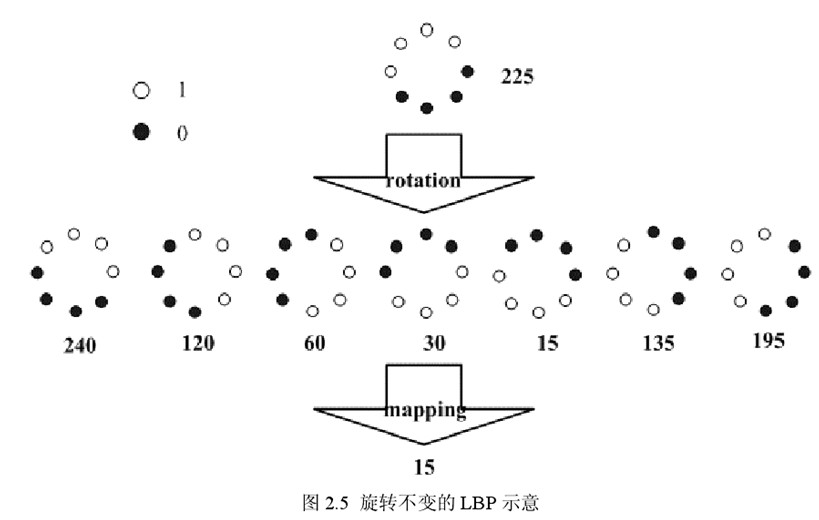
（3）LBP等价模式

     后来研究人员发现从00000000到11111111的值还是太多了，而研究发现大部分LBP的模式中的数字的变化都不会超过两次（10001111为变化了两次一次1到0 ，一个0到1,  00001111也是两次，要将他们看成首尾相连的），绝大部分都是形如10000111的这样的，而这样的数字就58个，将超过变化超过两次的剩余的198（注： 256 - 58）个LBP模式归为第59类，这样就减少了很多的计算量，注：那58个LBP模式列于文章尾部

2、LBP特征用于检测的原理（LZ在这一块卡了很久很久，大部分博文都没讲这一点，而这一块zouxy09讲的特别好，给我以豁然开朗的感觉，就直接复制粘贴了）

       显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。

        LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。

       因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；

        例如：一幅100*100像素大小的图片，划分为10*10=100个子区域（可以通过多种方式来划分区域），每个子区域的大小为10*10像素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10*10个子区域，也就有了10*10个统计直方图，利用这10*10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

　　而实际检测人脸时，因为不同块的表示人脸的贡献值不同，如眼睛的LBP的统计直方图对识别人脸的贡献明显要比光秃秃的额头的贡献大，在检测到人脸的情况下，我们通常给不同位置的块不同的权重来提高人脸识别的准确率，下面给出一组7*7时用到的权重模板的例子

2,1,1,1,1,1,2,
2,4,4,1,4,4,2,
1,1,1,0,1,1,1,
0,1,1,0,1,1,0,
0,1,1,1,1,1,0,
0,1,1,2,1,1,0,
0,1,1,1,1,1,0

3、对LBP特征向量进行提取的步骤

（1）首先将检测窗口划分为16×16的小区域（cell）；

（2）对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；

（3）然后计算每个cell的直方图，即每个数字（假定是十进制数LBP值）出现的频率；然后对该直方图进行归一化处理。

（4）最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；

然后便可利用SVM或者其他机器学习算法进行分类了。

在这里列出那58个uniform patterns.

00000000,0
00000001,1
00000010,2
00000011,3
00000100,4
00000110,6
00000111,7
00001000,8
00001100,12
00001110,14
00001111,15
00010000,16
00011000,24
00011100,28
00011110,30
00011111,31
00100000,32
00110000,48
00111000,56
00111100,60
00111110,62
00111111,63
01000000,64
01100000,96
01110000,112
01111000,120
01111100,124
01111110,126
01111111,127
10000000,128
10000001,129
10000011,131
10000111,135
10001111,143
10011111,159
10111111,191
11000000,192
11000001,193
11000011,195
11000111,199
11001111,207
11011111,223
11100000,224
11100001,225
11100011,227
11100111,231
11101111,239
11110000,240
11110001,241
11110011,243
11110111,247
11111000,248
11111001,249
11111011,251
11111100,252
11111101,253
11111110,254
11111111,255

十进制数位：

[0, 1, 2, 3, 4, 6, 7, 8, 12, 14, 15, 16, 24, 28, 30, 31, 32, 48, 56, 60, 62, 63, 64, 96, 112, 120, 124, 126, 127, 128, 129, 131, 135, 143, 159, 191, 192, 193, 195, 199, 207, 223, 224, 225, 227, 231, 239, 240, 241, 243, 247, 248, 249, 251, 252, 253, 254, 255]