数据结构-树
一、回顾基本概念
树
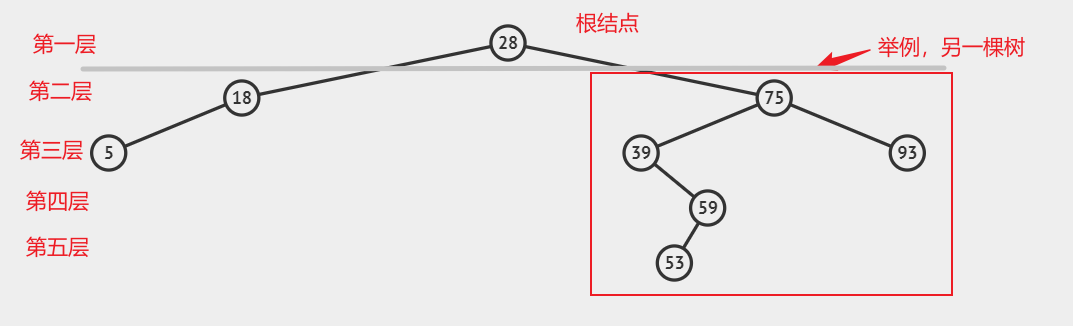
每个结点有零或多个子节点，没有父结点的结点后称为根结点，除了根结点每个子结点可以分为多个不相交的子树。
结点层次：根结点为第一层，其子结点为第二层，依次递推
结点深度：从根结点向下累加
结点高度：从叶结点向上累加
树的高度：为结点最大层数，图中为5
森林：互不相交的树的集合（把根节点去掉就是森林了）
二叉树
每个结点最多有两棵子树，且结点有左右之分。二叉树的左子树和右子树也是二叉树。根据二叉树的状态又有几个特殊的子树。
斜二叉树
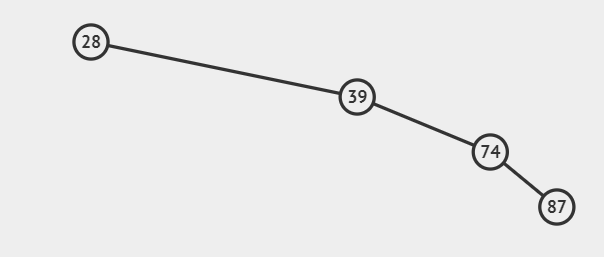
这也是后续要尽量避免的情形，失去了树的意义。
满二叉树
高度h，则结点为2h-1的树为满二叉树，也就是每一层都是满的。
完全二叉树
不一定满，只有最后一层可能不满，且不会有间隔。
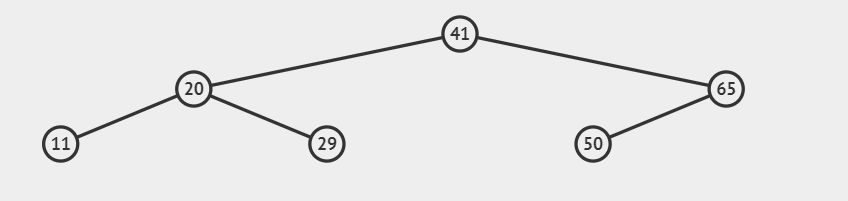
二叉查找树
别名：二叉搜索树、二叉排序树、BST
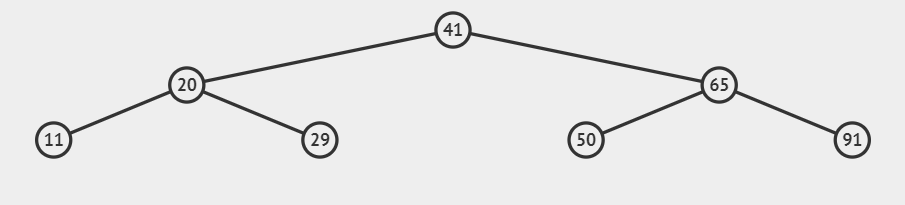
一个结点A，左边结点要么为空，要么小于结点A；右边结点要么为空，要么大于结点A。没有键值相等的结点。
上图就是一个二叉查找树。
平衡二叉树
特殊的二叉搜索树，一个结点左右子树高度差不超过1。上图其实还是一个平衡二叉树。
二、二叉树的遍历
存储方式
二叉树的存储有如下方法：
数组：适合完全二叉树，普通的二叉树（可能是斜二叉树）空间浪费大。
父结点指针、子结点指针。本文选用子结点指针。
class Node {
int data;
Node left;
Node right;
}
前、中、后序遍历
先序：考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)
中序：考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)
后序：考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)
以二叉查找树为例。BST首先应该有根结点和插入方法。二叉查找树插入：小于当前结点插入左边，否则右边。
public class BST {
// 根结点
Node root = null;
// 插入二叉搜索树
public boolean insert(int data) {
if(root==null) {
root = new Node(data);
return true;
}
Node n = root;
while (true) {
if (data<n.data) {="" if(n.left="=null)" n.left="new" node(data);="" return="" true;="" }="" else="" n="n.left;" if(data="=" n.data)="" bst没有键值相等的="" false;="" if(n.right="=null)" n.right="new" ```="" 遍历接口，选择前中后序遍历。="" ```java="" public="" void="" traverse(string="" method)="" switch="" (method)="" case="" "preorder":="" preordertraverse(root);="" break;="" "postorder":="" postordertraverse(root);="" "inorder":="" inordertraverse(root);="" default:="" system.out.println("preorder、postorder、inorder，输入无效，按preorder非递归遍历");="" preordertraverse();="" 测试插入：="" static="" main(string[]="" args)="" bst="" bst();="" bst.insert(3);="" bst.insert(6);="" bst.insert(9);="" bst.insert(2);="" bst.insert(1);="" bst.insert(10);="" bst.insert(7);="" bst.traverse("inorder");="" 1="" 2="" 3="" 6="" 7="" 9="" 10="" 如图：="" ![image-20211020113408623](https:="" gitee.com="" hqinglau="" img="" raw="" master="" 20211020113408.png)="" ####="" 前序遍历="" 考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)="" 递归方法比较明了，如下：="" private="" preordertraverse(node="" n)="" if(n="=null)" return;="" system.out.println(n.data);="" preordertraverse(n.left);="" preordertraverse(n.right);="" 非递归方法：输出一个结点的值后，要遍历其左子树，完了之后还要回来遍历它的右子树，所以应该有个栈存放遍历过的结点。="" 非递归方法：="" preordertraverse()="" if(root="=null)" stack<node=""> stack = new Stack<>();
System.out.println(root.data); // 输出
stack.push(root); // 压栈，遍历左子树，完了弹出栈，遍历右子树
Node cur = root;
while(true) {
if(cur.left!=null) {
System.out.println(cur.left.data);
stack.push(cur.left);
cur = cur.left;
}
else {
do {
if(stack.empty()) {
return;
}
cur = stack.pop().right;
} while (cur==null);
System.out.println(cur.data);
stack.push(cur);
}
}
}
如图：
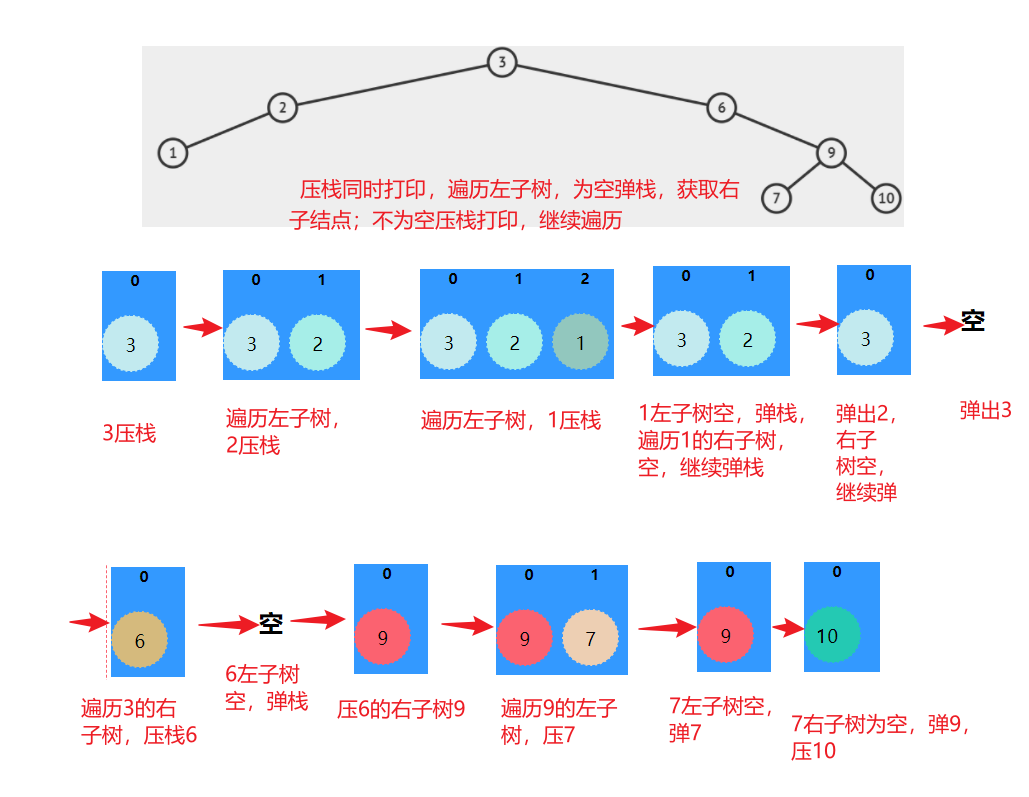
中序遍历
考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)
递归方法：
private void inOrderTraverse(Node n) {
if(n==null) {
return;
}
inOrderTraverse(n.left);
System.out.println(n.data);
inOrderTraverse(n.right);
}
非递归方法：
private void inOrderTraverse() {
if(root==null) {
return;
}
Stack<node> stack = new Stack<>();
stack.push(root); // 压栈，遍历左子树，打印当前结点，完了弹出栈，遍历右子树
Node cur = root;
while(true) {
if(cur.left!=null) {
stack.push(cur.left);
cur = cur.left;
}
else {
do {
if(stack.empty()) {
return;
}
Node n = stack.pop();
System.out.println(n.data);
cur = n.right;
} while (cur==null);
stack.push(cur);
}
}
}
后序遍历
递归方法：
private void postOrderTraverse(Node n) {
if(n==null) {
return;
}
postOrderTraverse(n.left);
postOrderTraverse(n.right);
System.out.println(n.data);
}
层序遍历
用队列存一层的结点。读的时候从头依次读取，左右子结点依次存取。
public void levelOrderTraverse() {
if(root==null) {
return;
}
Queue<node> stack = new LinkedList<>();
stack.add(root); // 压栈，遍历左子树，完了弹出栈，遍历右子树
int lastLayer = 1;
int n = 0;
while(!stack.isEmpty()) {
for(int i=0;i<lastlayer;i++) {="" node="" system.out.println(node.data);="" if(node.left!="null)" n++;="" stack.add(node.left);="" }="" if(node.right!="null)" stack.add(node.right);="" lastlayer="n;" n="0;" ```="" ##="" 三、二叉搜索树="" ###="" 二叉搜索树="" ####="" 插入="" 见第二节的存储方式部分。="" 删除="" 如要删除6结点="" <img="" src="https://gitee.com/hqinglau/img/raw/master/img/20211020160635.png" alt="image-20211020160635608" style="zoom:80%;">
按照递归思路比较容易，找到了就处理，找不到就分配给子函数处理。找到之后，如果是左树为空或右树为空，直接挂上，都不为空需要找到右子树的最小结点，赋值给根结点，然后删除最小结点。
```java
private Node remove(Node r, int data) {
if(r==null) return null;
if(data>r.data) {
r.right = remove(r.right,data);
} else if(data<r.data) {="" r.left="remove(r.left,data);" }="" else="" root="" 的data="=" data="" if(r.left="=null)" r="r.right;" if="" (r.right="=" null)="" 把右子树最小结点提到根结点，然后删除这个最小结点="" node="" minnode="r.right;" while(minnode.left!="null)" r.data="minNode.data;" r.right="remove(r.right,minNode.data);" return="" r;="" ```="" ####="" 查找="" 小往左子树找，大往右子树找。最大查找时间为树的高度。="" ###="" 平衡二叉树="" 普通二叉搜索树问题：极端情况会退化成线性。="" ![image-20211020133555445](https:="" gitee.com="" hqinglau="" img="" raw="" master="" 20211020133555.png)="" 平衡二叉树在修改时借助**旋转操作**，左右子树高度差不超过1，避免了这一问题。如图所示，要在该树种插入9，会破坏平衡：="" ![image-20211020163051980](https:="" 20211020163052.png)="" 旋转="" ![image-20211020164728884](https:="" 20211020164728.png)="" 左旋：以**右子树结点为轴**，动左边的x结点，旋转过程接收y的左子树作为右结点。右旋同理。="" 上图中，左旋之后，a的深度+1，c的深度-1。所以：**可以通过合适的左旋和右旋操作，调整二叉树的深度。**="" ll插入="" 对的左儿子的左子树进行一次插入（左左）：根结点右旋="" ![image-20211020165340908](https:="" 20211020165340.png)="" lr插入="" lr问题，对根结点左儿子右子树的插入问题：="" <img="" src="https://gitee.com/hqinglau/img/raw/master/img/20211020172401.png" alt="image-20211020172401514" style="zoom:80%;">
#### RR插入
LL插入的镜像问题，右边可能过深，对整体来一次左旋。
#### RL插入
LR问题的镜像问题，先对右子树右旋，再整体左旋。
#### 代码实现
按常规插入后调整。
```java
public class AVL {
Node root;
public int getHeight(Node r) {
if (r == null) return 0;
return Math.max(getHeight(r.left), getHeight(r.right)) + 1;
}
public Node rotateLeft(Node r) {
Node t = r.right;
r.right = t.left;
t.left = r;
return t;
}
public Node rotateRight(Node r) {
Node t = r.left;
r.left = t.right;
t.right = r;
return t;
}
public void insert(int data) {
root = insert(root,data);
Node left = root.left;
Node right = root.right;
if(left!=null) {
if(getHeight(left.left)-getHeight(left.right)>=2) {
root.left = rotateRight(left);
} else if(getHeight(left.right)-getHeight(left.left)>=2) {
root.left = rotateLeft(left);
}
}
if(right!=null) {
if(getHeight(right.left)-getHeight(right.right)>=2) {
root.right=rotateRight(right);
} else if(getHeight(right.right)-getHeight(right.left)>=2) {
root.right=rotateLeft(right);
}
}
if(getHeight(left)-getHeight(right)>=2) {
root=rotateRight(root);
} else if(getHeight(right)-getHeight(left)>=2) {
root=rotateLeft(root);
}
}
public Node insert(Node r, int data) {
if (r == null) {
return new Node(data);
}
if (data > r.data) {
r.right = insert(r.right, data);
} else if (data < r.data) {
r.left = insert(r.left, data);
}
return r;
}
}
四、红黑树简述
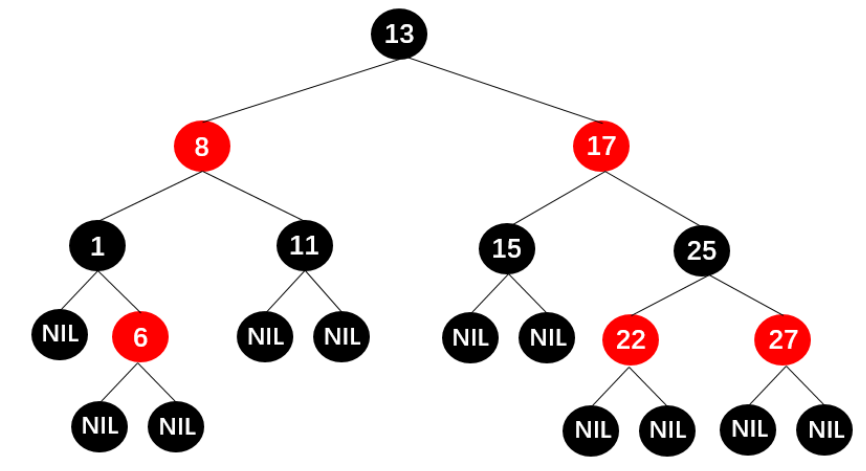
有了平衡二叉树，为何还要红黑树？
AVL插入时，几乎都需要旋转操作维持平衡。红黑树牺牲严格的平衡，换取插入/删除时的性能。
红黑树规则
规则一：结点非黑即红
规则二：根结点为黑色
规则三：叶结点的子结点（null）为黑色
规则四：红色结点的子结点为黑色
规则五：每个结点到null结点的所有路径，包含相同数目的黑色结点（相同的黑色高度）
如上图中17到nil结点，黑色结点数都是2。
这5条约束保证了：从根结点到叶子结点的最长路径，不会超过最短路径的两倍。由规则5具有相同的黑色高度，最短路径就全是黑色，最长路径黑红相间，而红色子结点为黑色，即不大于最短路径的两倍。
三种变换
插入后不破坏规则，不需要旋转变色，破坏规则需要调整。
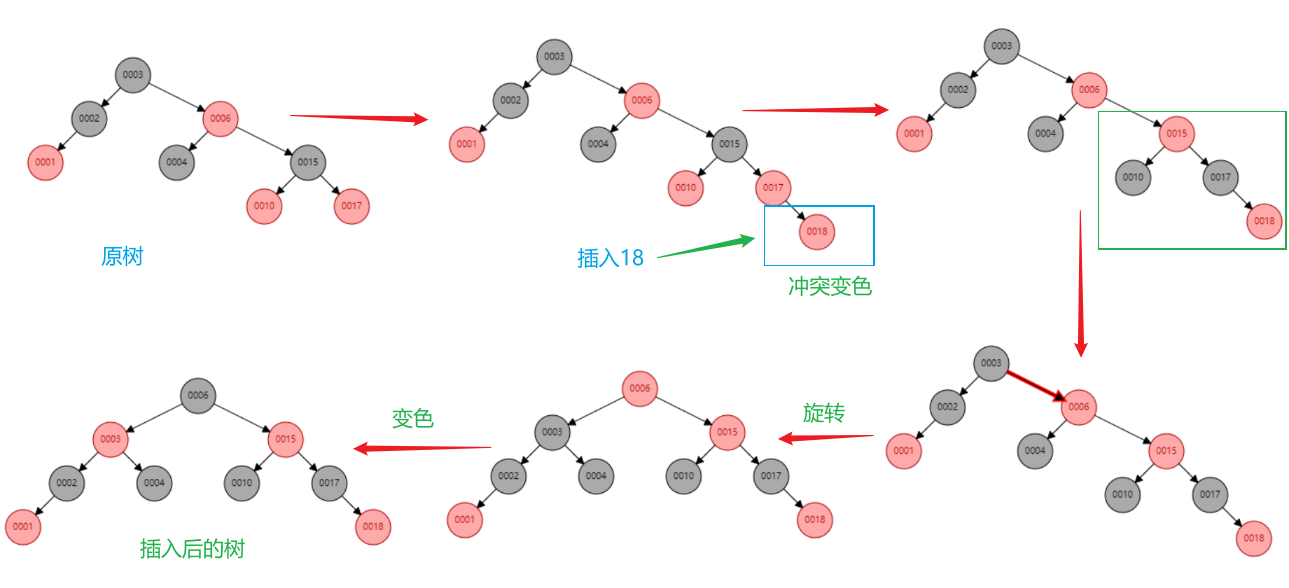
变色
插入结点一般选择红色，因为黑色由于规则五：相同黑色高度问题，很难调整。红红相连问题可通过变色和旋转解决。
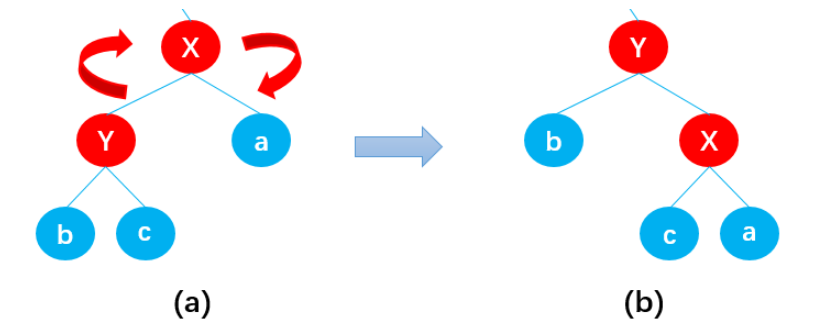
左旋
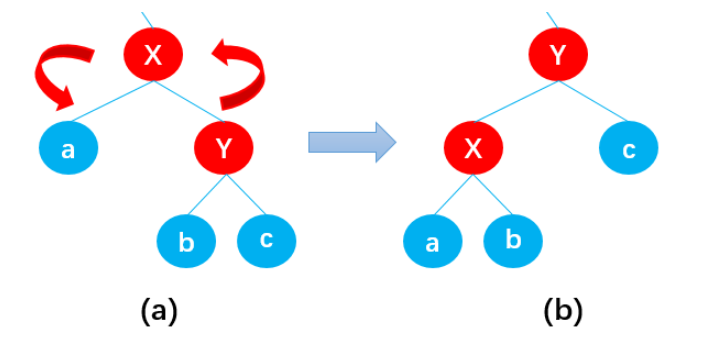
和之前的平衡二叉树左旋、右旋是一样的。
右旋
