20182316胡泊 《数据结构与面向对象程序设计》实验9报告
20182316胡泊 2019-2020-1 《数据结构与面向对象程序设计》实验9报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 胡泊
学号:20182316
实验教师:王志强
实验日期:2019年
必修/选修: 必修
实验内容
完成图的综合实践
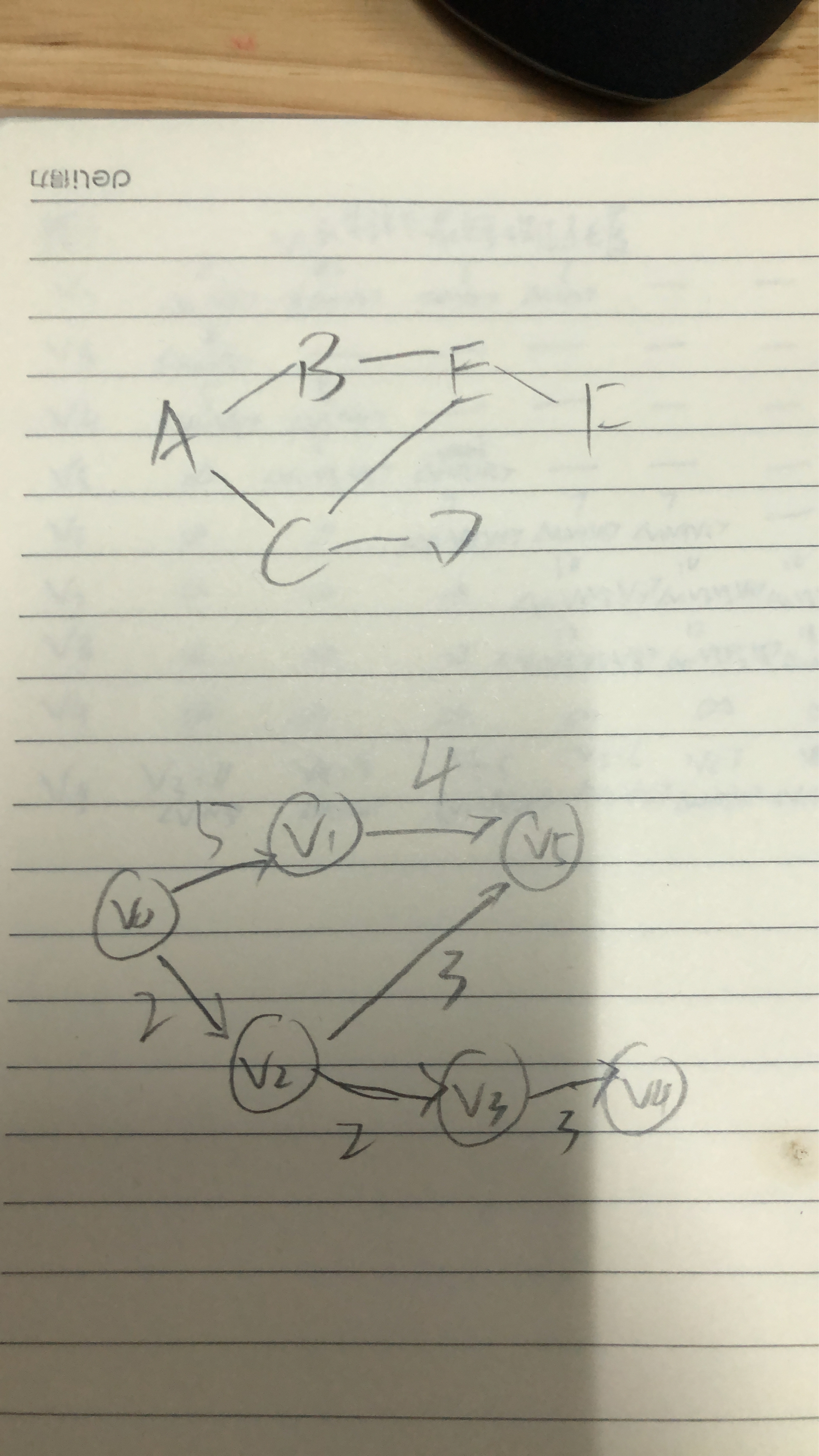
- (1)初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
- (2)图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
- (3)完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
- (4)完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
- (5)完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
实验过程及结果
1.初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
代码:
public Sorting(char[] dingdian, EData[] bian) {
int lenv = dingdian.length;
int elen = bian.length;
// 初始化顶点
mV= new N[lenv];
for (int i = 0; i < mV.length; i++) {
mV[i] = new N();
mV[i].dingdian = dingdian[i];
mV[i].firstX = null;
}
// 初始化边
Enum = elen;
for (int i = 0; i < elen; i++) {
// 读取顶点
char c1 = bian[i].start;
char c2 = bian[i].end;
int weight = bian[i].weight;
int p1 = gPs(c1);
int p2 = gPs(c2);
B node1 = new B ();
node1.i = p2;
node1.w = weight;
//连接
if(mV[p1].firstX == null)
mV[p1].firstX = node1;
else
Connect(mV[p1].firstX, node1);
B node2 = new B ();
node2.i = p1;
node2.w = weight;
//连接
if(mV[p2].firstX == null)
mV[p2].firstX = node2;
else
Connect(mV[p2].firstX, node2);
}
}
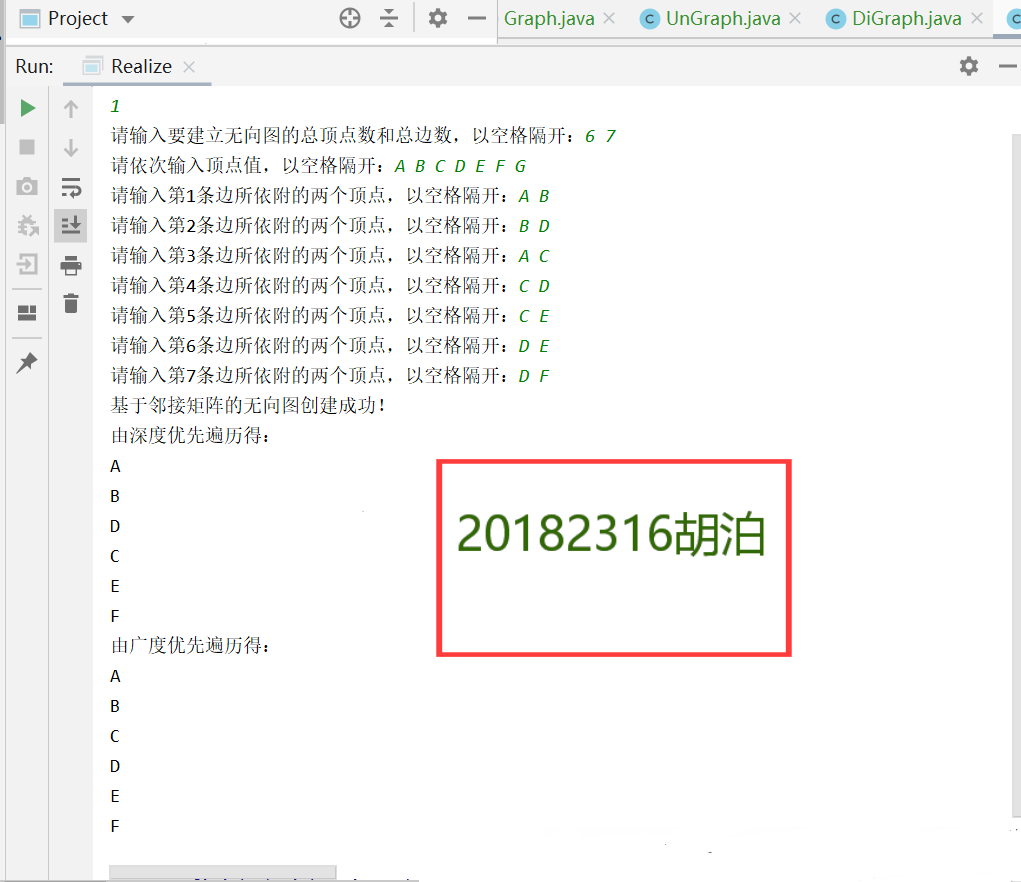
2.图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
- 深度优先遍历
private void DFS(int i, boolean[] BL) {
B node;
BL[i] = true;
System.out.printf("%c ", mV[i].dingdian);
node = mV[i].firstX;
while (node != null) {
if (!BL[node.i])
DFS(node.i, BL);
node = node.nextX;
}
}
- 广度优先遍历
public void BFS() {
int head = 0;
int rear = 0;
int[] queue = new int[mV.length]; // 辅组队列
boolean[] BL = new boolean[mV.length]; // 顶点访问标记
for (int i = 0; i < mV.length; i++)
BL[i] = false;
System.out.printf("广度优先遍历: ");
for (int i = 0; i < mV.length; i++) {
if (!BL[i]) {
BL[i] = true;
System.out.printf("%c ", mV[i].dingdian);
queue[rear++] = i; // 入队列
}
while (head != rear) {
int j = queue[head++]; // 出队列
B node = mV[j].firstX;
while (node != null) {
int k = node.i;
if (!BL[k])
{
BL[k] = true;
System.out.printf("%c ", mV[k].dingdian);
queue[rear++] = k;
}
node = node.nextX;
}
}
}
System.out.printf("\n");
}
3.完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
- 拓扑排序定义: 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
- 通常,这样的线性序列称为满足拓扑次序(TopoiSicai Order)的序列,简称拓扑序列。

代码:
public int TpSort() {
int index = 0;
int num = mV.length;
int[] ins; // 入度数组
char[] tops;
Queue<Integer> queue;
ins = new int[num];
tops = new char[num];
queue = new LinkedList<Integer>();
// 统计每个顶点的入度数
for(int i = 0; i < num; i++) {
B node = mV[i].firstX;
while (node != null) {
ins[node.i]++;
node = node.nextX;
}
}
// 将所有入度为0的顶点入队列
for(int i = 0; i < num; i ++)
if(ins[i] == 0)
queue.offer(i); // 入队列
while (!queue.isEmpty()) { // 队列非空
int j = queue.poll().intValue(); // 出队列。j是顶点的序号
tops[index++] = mV[j].dingdian;
B node = mV[j].firstX;
while(node != null) {
// 入度减1。
ins[node.i]--;
// 若入度为0,则入队列
if( ins[node.i] == 0)
queue.offer(node.i); // 入队列
node = node.nextX;
}
}
if(index != num) {
System.out.printf("有向有环图\n");
return 1;
}
// 打印拓扑排序结果
System.out.printf("拓扑排序: ");
for(int i = 0; i < num; i ++)
System.out.printf("%c ", tops[i]);
System.out.printf("\n");
return 0;
}
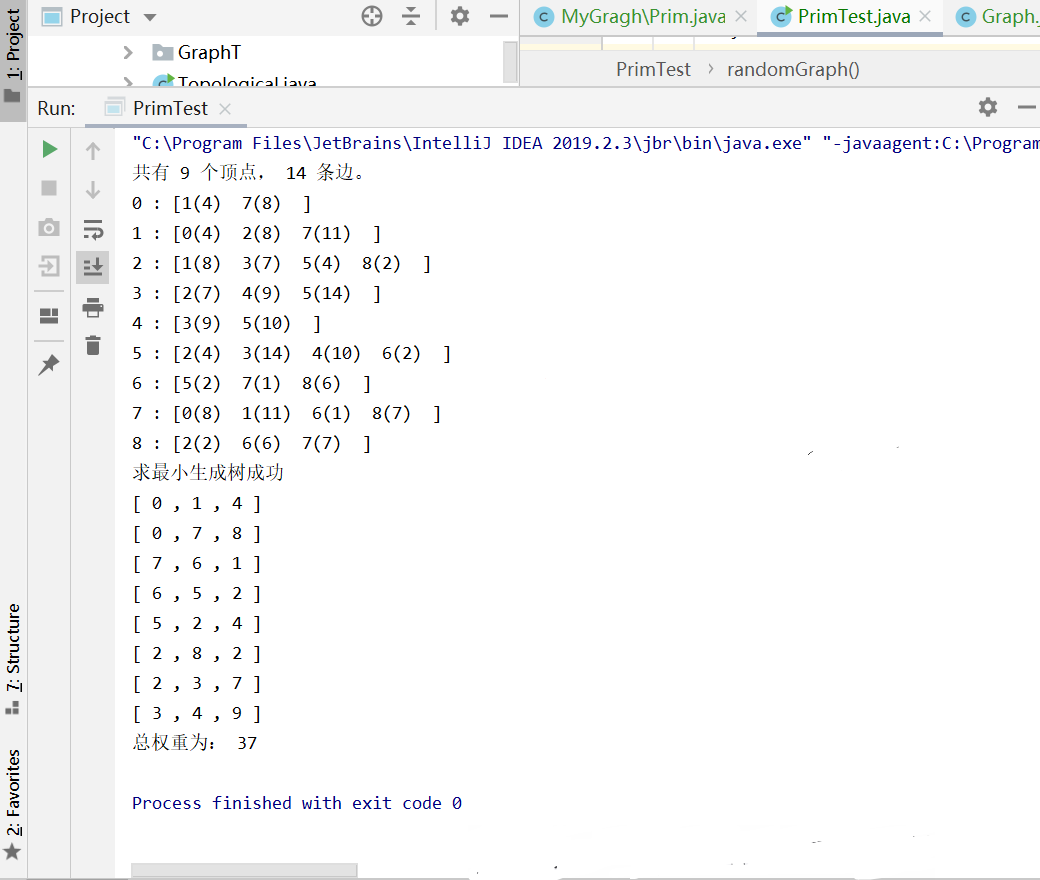
4.完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出
代码:
public void kruskal() {
int index = 0;
int[] v = new int[Enum]; // 保存终点。
EData[] rets = new EData[Enum]; // 暂存结果数组
EData[] e; // 对应的所有边
e = getEdges();
// 将边按权排序
sortEdges(e, Enum);
for (int i=0; i<Enum; i++) {
int p1 = gPs(e[i].start);
int p2 = gPs(e[i].end);
int m = getEnd(v, p1);
int n = getEnd(v, p2);
// 如果m!=n,则没有形成环路
if (m != n) {
v[m] = n;
rets[index++] = e[i];
}
}
}
5.完成有向图的单源最短路径求解(迪杰斯特拉算法)
代码:
public class DijstraAlgorithm {
public static void main(String[] args) {
int vertexNum = 5;
char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E' };
int[][] matrix = new int[][] { { 0, 10, Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 5 },
{ Integer.MAX_VALUE / 2, 0, 1, Integer.MAX_VALUE / 2, 2 },
{ Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 0, 4, Integer.MAX_VALUE / 2 },
{ 7, Integer.MAX_VALUE / 2, 6, 0, Integer.MAX_VALUE / 2 },
{ Integer.MAX_VALUE / 2, 3, 9, 2, 0 } }; // matrix[i][j]为0表示i==j,matrix[i][j]为Integer.MAX_VALUE/2表示两个顶点不是图的边,否则表示边的权值
Graph g = new Graph(vertexNum, vertexs, matrix);
Scanner sc = new Scanner(System.in);
int srcIndex;
do{
System.out.print("请输入起点(0~4):");
srcIndex = sc.nextInt();
}while(srcIndex < 0 || srcIndex > 4);
System.out.println(g.vertexs[srcIndex] + "作为源点");
Info info = dijkstra(g, srcIndex); // 指定将索引为srcIndex的顶点作为源点
for(int i : info.pathSerials){
System.out.print(g.vertexs[i] + " ");
}
System.out.println();
int index = 0;
for(int[] path : info.paths){
for(int i : path){
System.out.print(g.vertexs[i]);
}
System.out.println(": " + info.distances[index++]);
}
sc.close();
}
// 通过迪杰斯特拉(Dijkstra)算法求以vertex[srcIndex]顶点作为源点到其余各顶点的最短路径
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}
// 找到图中仍未加入到最短路径序列顶点集中到源点距离最小的顶点的索引
public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}
// 得到指定顶点i的从源点到顶点i的最短路径(均以顶点集vertexs中索引表示)
public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}
public static ArrayList<int[]> getPathOfAll(int[] path, int[] pathSerials){
ArrayList<int[]> paths = new ArrayList<int[]>();
for(int i = 0; i < pathSerials.length; i++){
paths.add(getPath(path, i));
}
return paths;
}
public static class Graph{
private int vertexNum;
private char[] vertexs;
private int[][] matrix;
private boolean visited[];
public Graph(int vertexNum, char[] vertexs, int[][] matrix){
this.vertexNum = vertexNum;
this.vertexs = vertexs;
this.matrix = matrix;
visited = new boolean[vertexNum];
}
}
public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
}
上传码云
实验过程中遇到的问题和解决过程
- 问题:迪杰斯特拉算法实现对我来说太困难了
- 问题解决方法:
- 基本思想:设置一个集合S存放已经找到最短路径的顶点,S的初始状态只包含源点v,对vi∈V-S,假设从源点v到vi的有向边为最短路径。以后每求得一条最短路径v, …, vk,就将vk加入集合S中,并将路径v, …, vk , vi与原来的假设相比较,取路径长度较小者为最短路径。重复上述过程,直到集合V中全部顶点加入到集合S中。
- 设计数据结构 :
- 1、图的存储结构:带权的邻接矩阵存储结构 。
- 2、数组dist[n]:每个分量dist[i]表示当前所找到的从始点v到终点vi的最短路径的长度。初态为:若从v到vi有弧,则dist[i]为弧上权值;否则置dist[i]为∞。
- 3、数组path[n]:path[i]是一个字符串,表示当前所找到的从始点v到终点vi的最短路径。初态为:若从v到vi有弧,则path[i]为vvi;否则置path[i]空串。
- 4、数组s[n]:存放源点和已经生成的终点,其初态为只有一个源点v。 - Dijkstra算法——伪代码
1 1. 初始化数组dist、path和s;
2 2. while (s中的元素个数<n)
3 2.1 在dist[n]中求最小值,其下标为k;
4 2.2 输出dist[j]和path[j];
5 2.3 修改数组dist和path;
6 2.4 将顶点vk添加到数组s中;
- Dijkstra算法——代码
public class DijstraAlgorithm {
public static void main(String[] args) {
int vertexNum = 5;
char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E' };
int[][] matrix = new int[][] { { 0, 10, Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 5 },
{ Integer.MAX_VALUE / 2, 0, 1, Integer.MAX_VALUE / 2, 2 },
{ Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 0, 4, Integer.MAX_VALUE / 2 },
{ 7, Integer.MAX_VALUE / 2, 6, 0, Integer.MAX_VALUE / 2 },
{ Integer.MAX_VALUE / 2, 3, 9, 2, 0 } }; // matrix[i][j]为0表示i==j,matrix[i][j]为Integer.MAX_VALUE/2表示两个顶点不是图的边,否则表示边的权值
Graph g = new Graph(vertexNum, vertexs, matrix);
Scanner sc = new Scanner(System.in);
int srcIndex;
do{
System.out.print("请输入起点(0~4):");
srcIndex = sc.nextInt();
}while(srcIndex < 0 || srcIndex > 4);
System.out.println(g.vertexs[srcIndex] + "作为源点");
Info info = dijkstra(g, srcIndex); // 指定将索引为srcIndex的顶点作为源点
for(int i : info.pathSerials){
System.out.print(g.vertexs[i] + " ");
}
System.out.println();
int index = 0;
for(int[] path : info.paths){
for(int i : path){
System.out.print(g.vertexs[i]);
}
System.out.println(": " + info.distances[index++]);
}
sc.close();
}
// 通过迪杰斯特拉(Dijkstra)算法求以vertex[srcIndex]顶点作为源点到其余各顶点的最短路径
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}
// 找到图中仍未加入到最短路径序列顶点集中到源点距离最小的顶点的索引
public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}
// 得到指定顶点i的从源点到顶点i的最短路径(均以顶点集vertexs中索引表示)
public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}
public static ArrayList<int[]> getPathOfAll(int[] path, int[] pathSerials){
ArrayList<int[]> paths = new ArrayList<int[]>();
for(int i = 0; i < pathSerials.length; i++){
paths.add(getPath(path, i));
}
return paths;
}
public static class Graph{
private int vertexNum;
private char[] vertexs;
private int[][] matrix;
private boolean visited[];
public Graph(int vertexNum, char[] vertexs, int[][] matrix){
this.vertexNum = vertexNum;
this.vertexs = vertexs;
this.matrix = matrix;
visited = new boolean[vertexNum];
}
}
public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
}
感悟
- 本次实验是图的最后一个实验,也是本学期最后一个实验,回顾这一学期的java和数据结构的学习,我收获颇丰,不仅学习了专业知识,更学习了学习方法,在遇到困难时如何高效解决,俗话说,授人以鱼不如授人以渔,而这些方法才是我在这门课中学到的最重要的东西。




