20182316胡泊 第9周学习总结
20182316胡泊 2019-2020-1 《数据结构与面向对象程序设计》第9周学习总结
教材学习内容总结
第十六章 树
什么是树
1.树的概念:
- 概念:我理解的树就是由内容和相互关系组成的非线性的存储数据的形式,具体来说就是由结点来存储元素,连线代表关系。
- 术语:
- 根:位于树的顶层的唯一结点,一棵树只有一个根结点。
- 双亲和孩子:一个结点只有一个双亲,但一个结点可以有多个孩子。
- 兄弟:有同一个双亲的多个结点相互为对方的兄弟。
- 叶子:没有孩子的结点称之为叶子。叶子不一定全部位于最底层。
- 内部结点:树中既不是根结点也不是叶结点的结点。
- 高度/深度:树的层数。
- 度/阶:一结点所具有的孩子数目。
2.树的分类
- 按度来划分
- n元树:树的每个结点的孩子数不超过n个孩子。
- 二叉树:每个结点最多有两个结点的数。
- 按树是否平衡来划分
- 平衡:树的所有叶子之间相差层数不超过一层的树称为平衡的树。
- 完全树:底层叶子都位于树的左边称为完全树,也就是底层节点只能将左边填满了才能放进右边。
- 满树:在一颗n元树中,所有叶子都位于一层,且除叶子外的每个结点都有n个孩子,则该树被称作满树。
树的遍历
- 前序遍历:从根结点开始,然后从左孩子开始访问每个结点的所有孩子。
public void preorder (ArrayList<T> iter) {
iter.add (element);
if (left != null)
left.inorder (iter);
if (right != null)
right.inorder (iter);
}
- 中序遍历:先访问根结点的左孩子,然后是根结点,最后是根结点的右孩子。
public void inorder(ArrayIterator<T> iter){
if(left != null)
left.inorder(iter);
iter.add(element);
if(right != null)
right.inorder(iter);
}
- 后序遍历:从左到右遍历所有孩子,最后访问根结点。
public void postorder(ArrayIterator<T> iter){
if(left != null)
left.postorder(iter);
if(right != null)
right.postorder(iter);
iter.add(element);
}
- 层序遍历:从根结点开始,从左至右访问每一层的所有结点。
public void levelorder(TreeNode root)
{
ArrayDeque<TreeNode> deque=new ArrayDeque<TreeNode>();
deque.add(root);//根节点入队
while(!deque.isEmpty()){
TreeNode temp=deque.remove();
System.out.print(temp.val+"--");
if(temp.left!=null){
deque.add(temp.left);
}
if(temp.right!=null){
deque.add(temp.right);
}
}
}
二叉树
- 二叉树中好用的性质(假设二叉树的根结点位于第1层)
- 二叉树的第i层最多有2^(i-1)个结点。
- 深度为k的二叉树最多有2^k-1个结点。
- 对任何一颗二叉树,如果其叶子个数为a,度为2的结点数为b,则有a=b+1。
- 具有n个结点的完全二叉树的高度为[log2n]+1
- 在数组中位置为n的元素,元素的左子结点存储在(2n+1)的位置,右子结点存储在(2*(n+1))的位置。
第十七章二叉查找树
-
概念:树中的所有结点,其左孩子都小于父结点,父结点小于或等于其右孩子。
-
性质:
- 任意结点的左、右子树也分别为二叉查找树;
- 没有元素相等的结点。
-
操作:
- addElement:向树中添加一个元素
- removeElement:从树中删除一个元素
- removeAllOccurrences:从树中删除所指定元素的任何存在
- removeMin:删除树中的最小元素
- removeMax:删除树中的最大元素
- findMin:返回树中的最小元素的引用(补全内容见课后pp17.1)
- findMax:返回树中的最大元素引用(补全内容见课后pp17.1)
二叉查找树实现
- 查找:
将所要查找的元素与根结点的元素进行比较,如果小于根结点则继续与左孩子对比,大于根结点则继续与右孩子对比,如果相等则返回元素。
递归实现
public void find(T element)
{
return find(root, element);
}
private void find(BinaryTreeNode root, T element)
{
if (root == null) {
return element;
}
int comparable = element.CompareTo(root.getElement);
if (comparable > 0){
find(root.right,element);
}
else if (comparable < 0){
find(root.left,element);
}
else {
return root.getElement;
}
}
-
插入:
- 若当前的二叉查找树为空,加入的元素会成为根结点。
- 若所插入结点的元素小于根结点的元素:
- 若根的左孩子为null,插入结点将会成为新的左孩子。
- 若根的左孩子不为null,则会继续对左子树进行遍历,遍历的同时进行比较操作。
- 若所插入结点的元素大于或等于根结点的元素
- 若根的右孩子为null,插入结点将会成为新的右孩子。
- 若根的右孩子不为null,则会继续对右子树进行遍历,遍历的同时进行比较操作。
-
删除
二叉查找树的删除我感觉很复杂,那一个二叉排序树实践的删除操作做了我两个小时。
我们先来讨论一下删除的情况:- 删除的为叶子结点:这种情况下可以直接删除该结点。
- 但是!这里有一个要注意的地方,那就是在删掉叶子结点时,我会理所当然的将这个结点=null,但是发现并没有删掉。后来,单步调试,发现在将其赋为null时,该结点的确等于了空,我思考后发现,其实我确实已经将它赋值为空,也就是将他的指针指向了空,但是当回到树中时,该节点的父节点的子指针依旧指向的是它原来的位置,所以并没有删掉该节点!!!
- 所以我改正了我的思路,令被删除结点的父结点的子结点为空就行了。
- 下面是我编写的找到父结点的方法:
- 删除的为叶子结点:这种情况下可以直接删除该结点。
public Leaf findparent(int a){
Leaf current=root;
Leaf parent;
while(true){
parent=current;
if(a<current.data){
current=current.left;
if(current.data==a){
break;
}
}
else if(a>current.data) {
current=current.right;
if(current.data==a){
break;
}
}
else
break;
}
return parent;
}
-
删除的结点只有左子树或右子树时,将所删除结点的父结点的指针指向所删除结点仅有的孩子。
-
所删除的结点既有左子树又有右子树
- 这里需要了解两个概念——前驱结点和后继结点。分别是将树中元素排好序后两个相邻的元素,当一个节点被删除时,为了保证二叉树的结构不被破坏,要让它的前驱结点或者后继结点来代替它的位置(将值赋给删除结点),然后将它的前驱结点或者后继结点做同样的删除操作。
- 三种情况的代码:
public void delete(int a){
Leaf current=find(a);
if(current.left==null&¤t.right==null){
Leaf parent = findparent(a);
if(parent.right==current){
parent.right=null;
}
else if(parent.left==current){
parent.left=null;
}
}
else if(current.right!=null&¤t.left!=null){
int p=findbefore(a);
delete(p);
current.data=p;
}
else if(current.left!=null&¤t.right==null) {
current.data=current.left.data;
current.left=null;
}
else{
current.data=current.right.data;
current.right=null;
}
}
平衡二叉查找树
- 使二叉查找树平衡的方法
- 不平衡:
- 插入元素或删除元素会使二叉查找树变得不平衡。
- 如果二叉查找树不平衡,其效率可能很低。
- 不平衡就是,最深叶结点与最浅的叶结点层数差不大于一。
- 为了使树达到平衡,有四种方法:右旋、左旋、右左旋和左右旋。
- 左旋和右旋
- 将根结点的左孩子/右孩子(与不平衡的子树相反的一方)成为新的根结点,然后使原树根的左孩子的右孩子(右孩子的左孩子)成为原树根的新的右孩子(左孩子)
- 右左旋和左右旋
- 我理解的右左旋和左右旋就是做多次左旋或右旋,因为在做了一次后,二叉树依然不平衡,因此要重复再做一次。
- 不平衡:
教材学习中的问题和解决过程
- 问题1:递归和迭代的区别在哪里?
- 问题1解决方案:
- 概念不同: 程序调用自身的编程技巧称为递归,其实就是函数自己调用自己。迭代是指利用变量的原值推算出变量的一个新值,如果递归是自己调用自己的话,迭代就是A不停的调用B。
- 使用的方法不同: 迭代使用的是循环(for,while,do-while)或者迭代器,当循环条件不满足时退出。而递归一般是函数递归,可以是自身调用自身,也可以是非直接调用,即方法A调用方法B,而方法B反过来调用方法A,递归退出的条件为if-else语句,当条件符合基的时候退出。
- 对比: 递归的代码比较简单易懂,实现一个计算逻辑往往只需要很短的代码就能解决。但是由于它要不停地调用函数,就可能浪费大量的空间。递归中函数调用的局部状态是用栈来记录的,所以如果递归太深的话还有可能导致堆栈溢出。而对于迭代而言,能使用递归实现的都可以使用迭代来实现,并且效率会很高,在空间消耗上也很小,唯一的缺点就是代码比较难懂。
- 总结: 递归中一定有迭代,但是迭代中不一定有递归,大部分可以相互转换。能用迭代的不要用递归,递归调用函数不仅浪费空间,如果递归太深的话还容易造成堆栈的溢出。
- 问题2:为什么二叉查找树不平衡,查找效率就会变低
- 问题2解决方法:
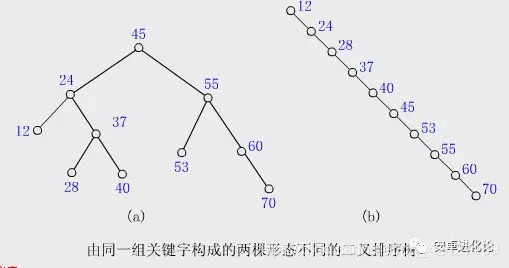
- 在最好的情况下,二叉排序树的查找效率比较高,是 O(logn),其效率近似于折半查找;
- 但最差时候会是 O(n),比如插入的元素是有序的,生成的二叉排序树就是一个链表,这种情况下,需要遍历全部元素才行(见下图 )。
- 问题3:书上决策树中提到的is-a关系是什么关系?
- 问题3解决方法:
- is-a(英语:subsumption,包含架构)指的是类的父子继承关系,例如类D是另一个类B的子类(类B是类D的父类)。换句话说,通常"D is-a B"(B把D包含在内,或是D被包含在B内)指的是,概念体D物是概念体B物的特殊化,而概念体B物是概念体D物的一般化。(百度百科)
- 我的理解:is-a,例如hupo is a student,胡泊是一个学生,胡泊就继承了学生的所有属性与功能,但胡泊是学生的一个特例,即胡泊同时还具有其他属性。
代码调试中的问题和解决过程
-
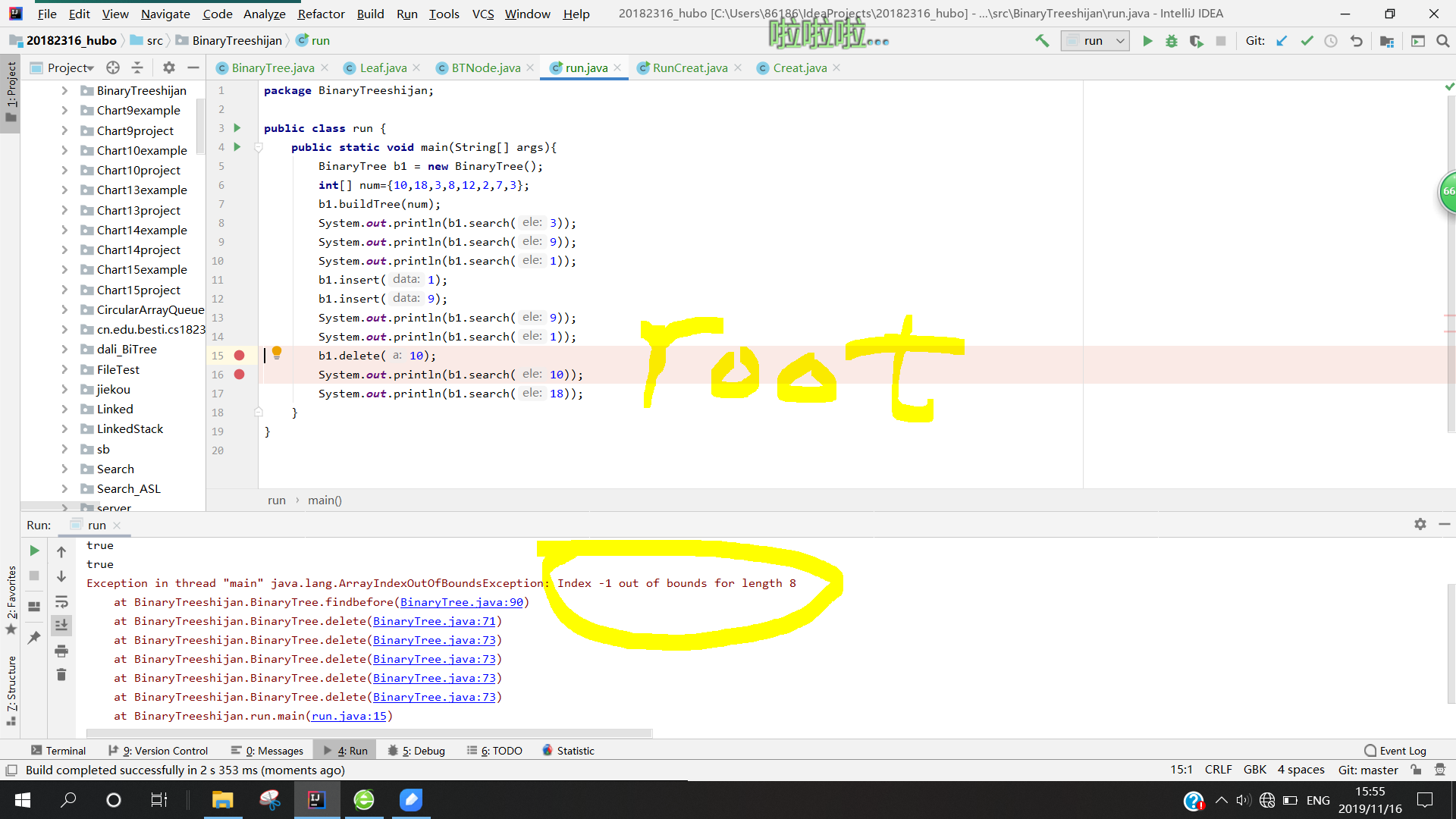
问题1:在做二叉树结点删除操作时,删掉叶子结点和仅有一个叉的结点时都很顺利,但是当删除有两个叉的结点时,出现了循环到数组(前驱结点)最小值的情况,最终导致数组下标溢出。
-
问题1解决方案:
-
原因:
- 删除有两个叉的结点的原理是找到该节点的前驱结点和它所在的位置,将前驱结点的值赋给被删除结点,这样不会破坏二叉查找树的性质,然后用同样的方法将前驱结点删除
- 但是,我在用同样的方法删除前驱结点时用了一个递归
else if(current.right!=null&¤t.left!=null){ int p=findbefore(a); current.data=p; delete(p); }代码的功能就是找到前驱结点,将值赋给删除结点,然后递归删除前驱结点(这里删的是值等于p的结点!!)
也就是说我在将前驱结点的值赋给了被删结点后,再调用delete方法删除值等于p的结点,于是就反复删除该结点,而真正要被删除的前驱结点却依然存在,最终导致一直滑到了最小的结点

-
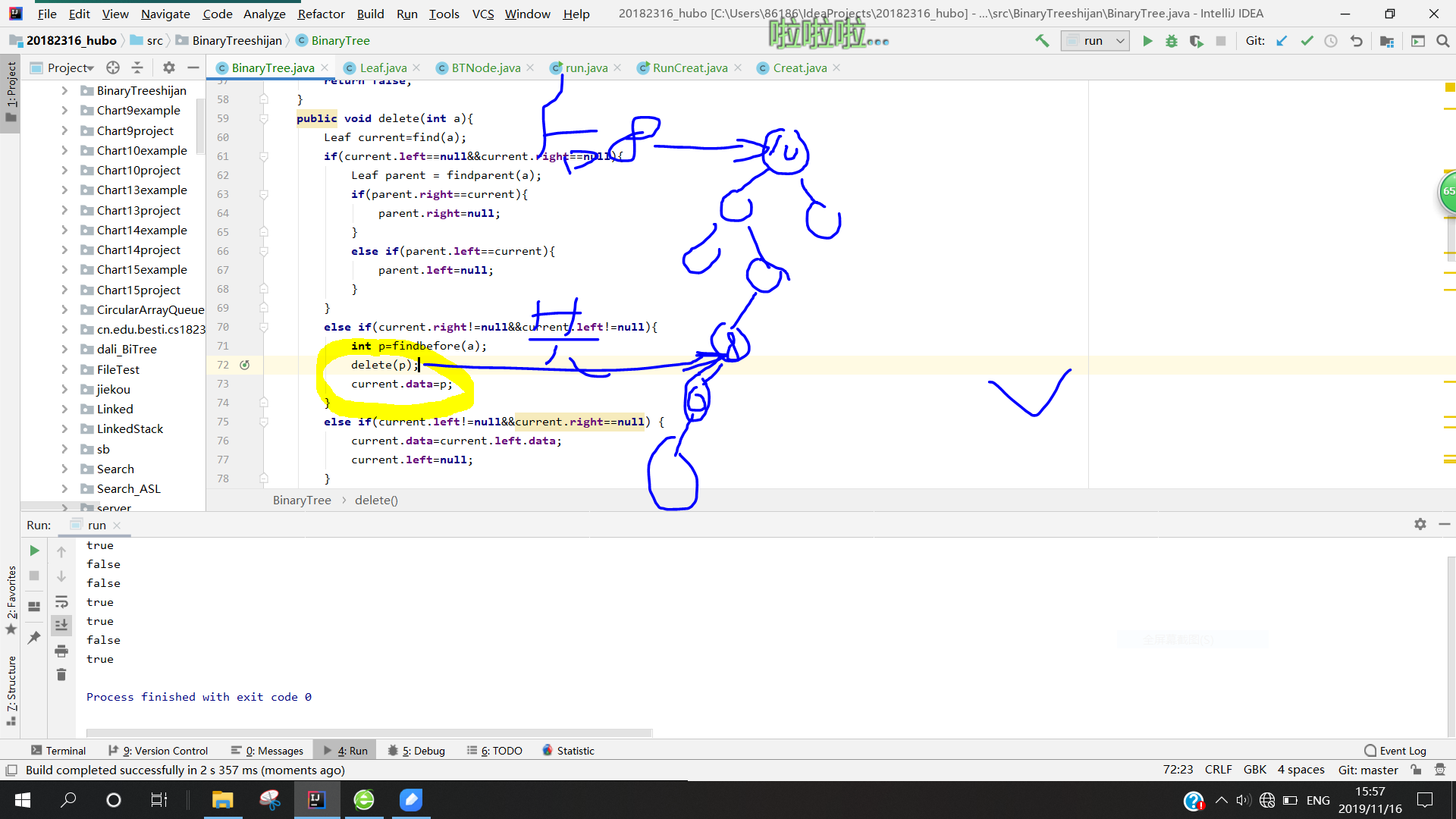
解决方法:找到了原因,解决它其实很简单,就是将删除与赋值的顺序反过来,先将前驱节点的值保存到变量p中,然后删除前驱结点,最后将p赋给被删结点,就完成了。代码如下:
else if(current.right!=null&¤t.left!=null){ int p=findbefore(a); delete(p); current.data=p; } -
-
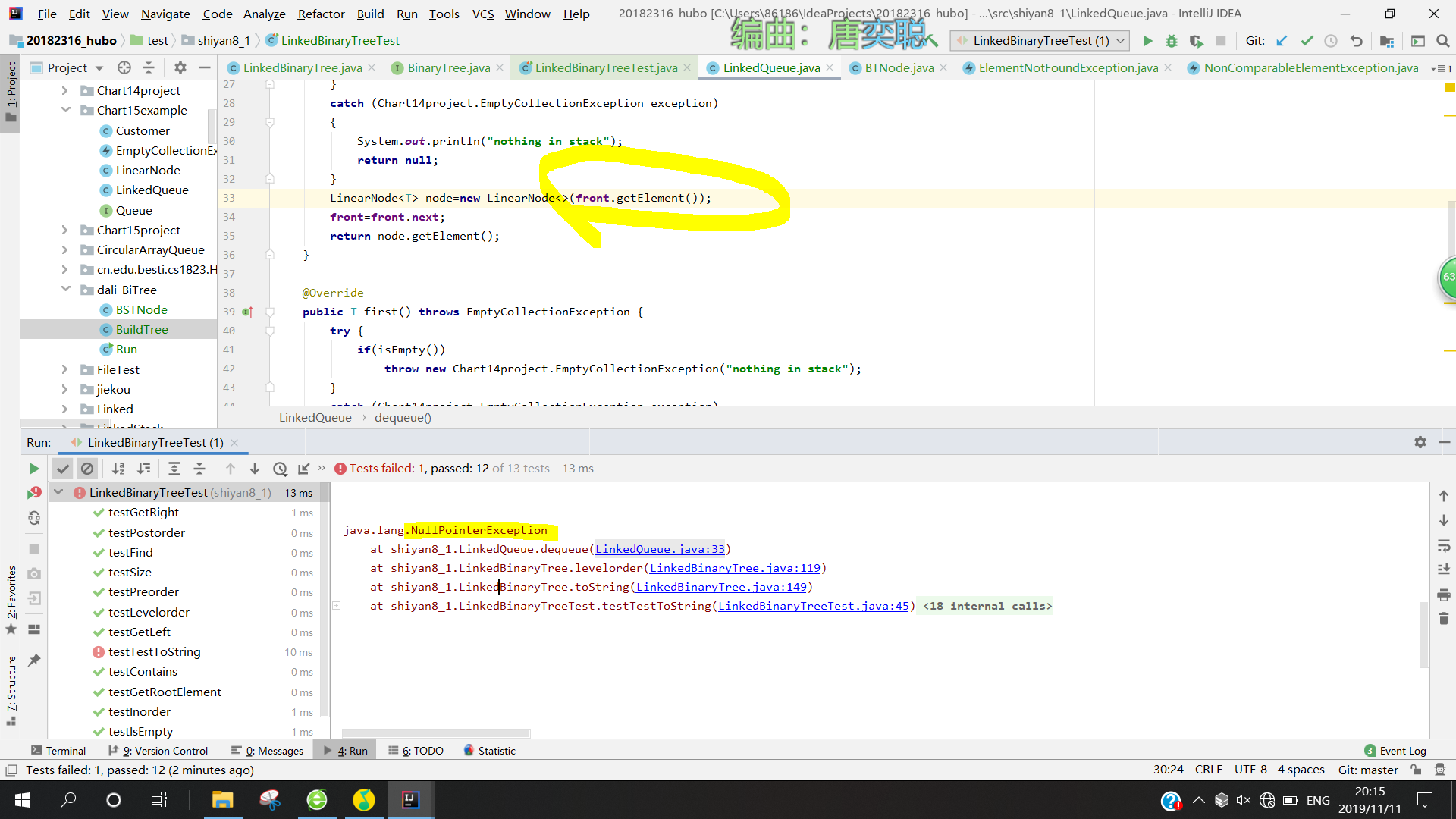
问题2:当我在调用队列头的数据时,出现了空指针报错
-
问题2解决方案:
- 抛出错误的提示说问题是出在LinkedBinaryTree里面的dequeue方法中,但是我非常不理解为什么抛出的会是NullPointerException。于是去查了一下会抛出NullPointerException异常的原因有哪些,一般有三种:字符串变量未初始化;接口类型的对象没有用具体的类初始化;当一个对象的值为空时,没有判断为空。
- 按照它的思路我想了很久,发现在之前代码中,我进行了一次队列元素增加,理论上front应该向前移了一位,但是我的front还是之前的,于是我将front作为参数传到了方法里面,就解决了。
代码托管
上周考试错题总结
1.In removing an element from a binary search tree, another node must be ___________ to replace the node being removed.
A .duplicated
B .demoted
C .promoted
D .None of the above
正确答案: C 我的答案: B
- 解析:当在二叉查找树上删除一个结点时,后面的结点需要向上移动来补全。当时,以为越靠近根结点说明深度越低,所以是降级了;但是看完答案好像人家的意思是向上补全。题意理解不准确哈哈
结对及互评
-
博客中值得学习的或问题:
- 对上周的错题进行了仔细的更正和课后复习,我对上周考试题的复习较为草率。
- 博客撰写详细,有理有据。
- 在撰写博客的过程中可以加入更多自己的理解。
-
代码中值得学习的或问题:
- 代码风格良好,便于阅读。
-
基于评分标准,我给本博客打分:14分。得分情况如下:
-
正确使用Markdown语法(加1分):
- 不使用Markdown不加分
- 有语法错误的不加分(链接打不开,表格不对,列表不正确...)
- 排版混乱的不加分
-
模板中的要素齐全(加1分)
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程(2分)
-
代码调试中的问题和解决过程(3分)
-
本周有效代码超过300分行的(加1分)
-
其他加分:
- 周五前发博客的加1分
- 感想,体会不假大空的加1分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
点评过的同学博客和代码
- 本周结对学习情况
-
结对照片
-
结对学习内容
对上周及本周的考试内容进行了探讨,并通过上网查询等方式深入分析,直到将问题理解。
一起制作博客,markdown,遇到问题相互询问,并解决。
其他(感悟、思考等,可选)
- 其实上周刚开始学树的时候感觉自己都是稀里糊涂的,代码也不是很懂会有很多错误,但是当时因为时间比较紧张所以都是赶着(上网借鉴)做完的,但是这周在学习新的东西的时候发现有些上一章我糊弄过去的东西如果不搞懂搞明白的话是做不出来的,所以又去返工把之前的东西搞明白,所以说学习还是要脚踏实地,真的一点都不能轻易放松。
- 当遇到代码问题时,一定要先思考,网上的不一定对,更不一定适合,实在不行了再上网百度。
学习进度条
| 代码行数(实际/预期) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | |||
| 第一周 | 119/119 | 3/3 | 20/20 | |
| 第二周 | 302/300 | 2/5 | 25/45 | |
| 第三周 | 780/800 | 2/7 | 25/70 | |
| 第四周 | 1500/1300 | 2/9 | 25/95 | |
| 第五周 | 3068/2500 | 3/12 | 25/120 | |
| 第六周 | 4261/4000 | 2/14 | 25/145 | |
| 第七、八周 | 7133/7000 | 3/17 | 25/170 | |
| 第九周 | 10330/10000 | 3/20 | 25/195 |
-
计划学习时间:25小时
-
实际学习时间:25小时




