20182316胡泊 实验7报告
20182316胡泊 2019-2020-1 《数据结构与面向对象程序设计》实验7报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 胡泊
学号:20182316
实验教师:王志强
实验日期:2019年
必修/选修: 必修
实验内容
1.定义一个Searching和Sorting类,并在类中实现linearSearch,SelectionSort方法,最后完成测试。
要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
2.重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1823.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1823.G2301)
把测试代码放test包中
3.参考http://www.cnblogs.com/maybe2030/p/4715035.html ,学习各种查找算法并在Searching中补充查找算法并测试
4.补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)
测试实现的算法(正常,异常,边界)
5.编写Android程序对实现各种查找与排序算法进行测试,提交运行结果截图
实验过程及结果
1.实现linearSearch,SelectionSort方法
- 用Junit测试的程序好久没用了,所以我参考了之前的程序才回想起来

2.把Sorting.java Searching.java放入包中,把测试代码放test包中,把测试代码放test包中即可(Ctrl c+Ctrl v)
3.学习各种查找算法并在Searching中补充查找算法并测试
以下是我学习的结果:
线性查找
- 顺序查找
- 顺序查找适合于存储结构为顺序存储或链接存储的线性表。
int SequenceSearch(int a[], int value, int n) { int i; for(i=0; i<n; i++) if(a[i]==value) return i; return -1; } - 二分查找
- 元素必须是有序的,如果是无序的则要先进行排序操作。
//二分查找(折半查找),版本1 int BinarySearch1(int a[], int value, int n) { int low, high, mid; low = 0; high = n-1; while(low<=high) { mid = (low+high)/2; if(a[mid]==value) return mid; if(a[mid]>value) high = mid-1; if(a[mid]<value) low = mid+1; } return -1; } //二分查找,递归版本 int BinarySearch2(int a[], int value, int low, int high) { int mid = low+(high-low)/2; if(a[mid]==value) return mid; if(a[mid]>value) return BinarySearch2(a, value, low, mid-1); if(a[mid]<value) return BinarySearch2(a, value, mid+1, high); } - 插值查找(折半查找的改进)
- 折半查找这种查找方式,不是自适应的
- 通过类比,也就是将上述的比例参数1/2改进为自适应的,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low),
//插值查找
int InsertionSearch(int a[], int value, int low, int high)
{
int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
if(a[mid]==value)
return mid;
if(a[mid]>value)
return InsertionSearch(a, value, low, mid-1);
if(a[mid]<value)
return InsertionSearch(a, value, mid+1, high);
}
- 斐波那契查找
- 也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。斐波那契查找也属于一种有序查找算法。
const int max_size=20;//斐波那契数组的长度
/*构造一个斐波那契数组*/
void Fibonacci(int * F)
{
F[0]=0;
F[1]=1;
for(int i=2;i<max_size;++i)
F[i]=F[i-1]+F[i-2];
}
/*定义斐波那契查找法*/
int FibonacciSearch(int *a, int n, int key) //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字
{
int low=0;
int high=n-1;
int F[max_size];
Fibonacci(F);//构造一个斐波那契数组F
int k=0;
while(n>F[k]-1)//计算n位于斐波那契数列的位置
++k;
int * temp;//将数组a扩展到F[k]-1的长度
temp=new int [F[k]-1];
memcpy(temp,a,n*sizeof(int));
for(int i=n;i<F[k]-1;++i)
temp[i]=a[n-1];
while(low<=high)
{
int mid=low+F[k-1]-1;
if(key<temp[mid])
{
high=mid-1;
k-=1;
}
else if(key>temp[mid])
{
low=mid+1;
k-=2;
}
else
{
if(mid<n)
return mid; //若相等则说明mid即为查找到的位置
else
return n-1; //若mid>=n则说明是扩展的数值,返回n-1
}
}
delete [] temp;
return -1;
}
int main()
{
int a[] = {0,16,24,35,47,59,62,73,88,99};
int key=100;
int index=FibonacciSearch(a,sizeof(a)/sizeof(int),key);
cout<<key<<" is located at:"<<index;
return 0;
}
非线性查找
-
二叉树表查找
- 对二叉查找树进行中序遍历,即可得到有序的数列。
- 在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷
-
后面的红黑二叉树老师说我们课时较少就先不用学了。
4.补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等,测试实现的算法
因为我记得上课并没有讲堆排序,所以我上网找了一个,并学习了他的思路。
5.编写Android程序对实现各种查找与排序算法进行测试,提交运行结果截图
- 将各种代码都粘到Android里面去,然后用mainactivity调用个个类,如果与预期结果一样则输出 successful!。
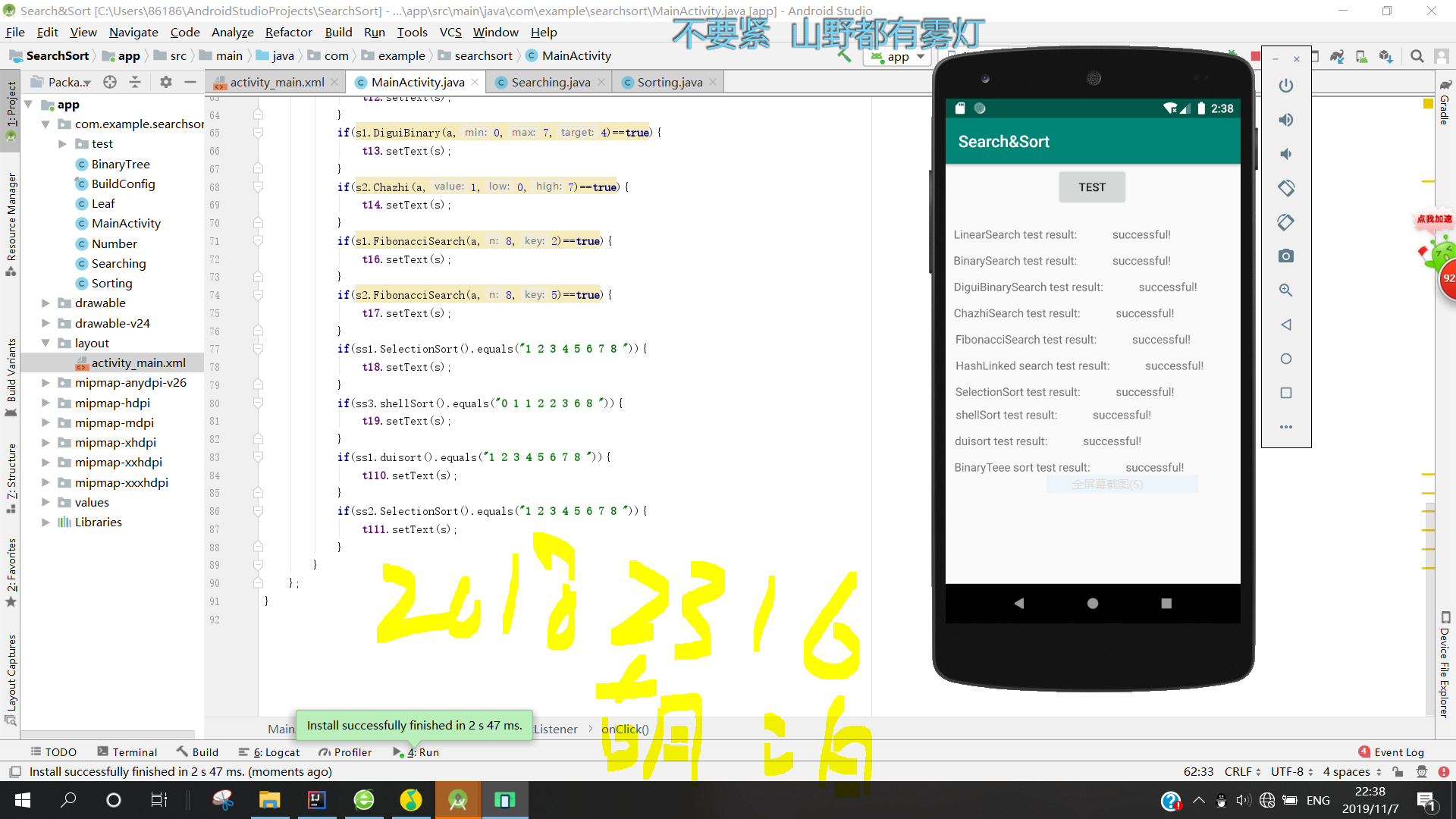
上传码云
实验过程中遇到的问题和解决过程
- 问题1:堆排序的优缺点
- 问题1解决方案:
- 优点:
- 堆排序的效率与快排、归并相同,都达到了基于比较的排序算法效率的峰值(时间复杂度为O(nlogn))
- 除了高效之外,最大的亮点就是只需要O(1)的辅助空间了,既最高效率又最节省空间,只此一家了
- 堆排序效率相对稳定,不像快排在最坏情况下时间复杂度会变成O(n^2)),所以无论待排序序列是否有序,堆排序的效率都是O(nlogn)不变(注意这里的稳定特指平均时间复杂度=最坏时间复杂度,不是那个“稳定”,因为堆排序本身是不稳定的)
- 缺点:最大的也是唯一的缺点就是堆在实际场景中的数据是频繁发生变动的,而对于待排序序列的每次更新(增,删,改),我们都要重新做一遍堆的维护,以保证其特性,这在大多数情况下都是没有必要的。(所以快排成为了实际应用中的老大,而堆排序只能在算法书里面顶着光环,当数据更新不很频繁的时候,当然堆排序更好些)
- 优点:
- 问题2:当我在调用队列头的数据时,出现了空指针报错
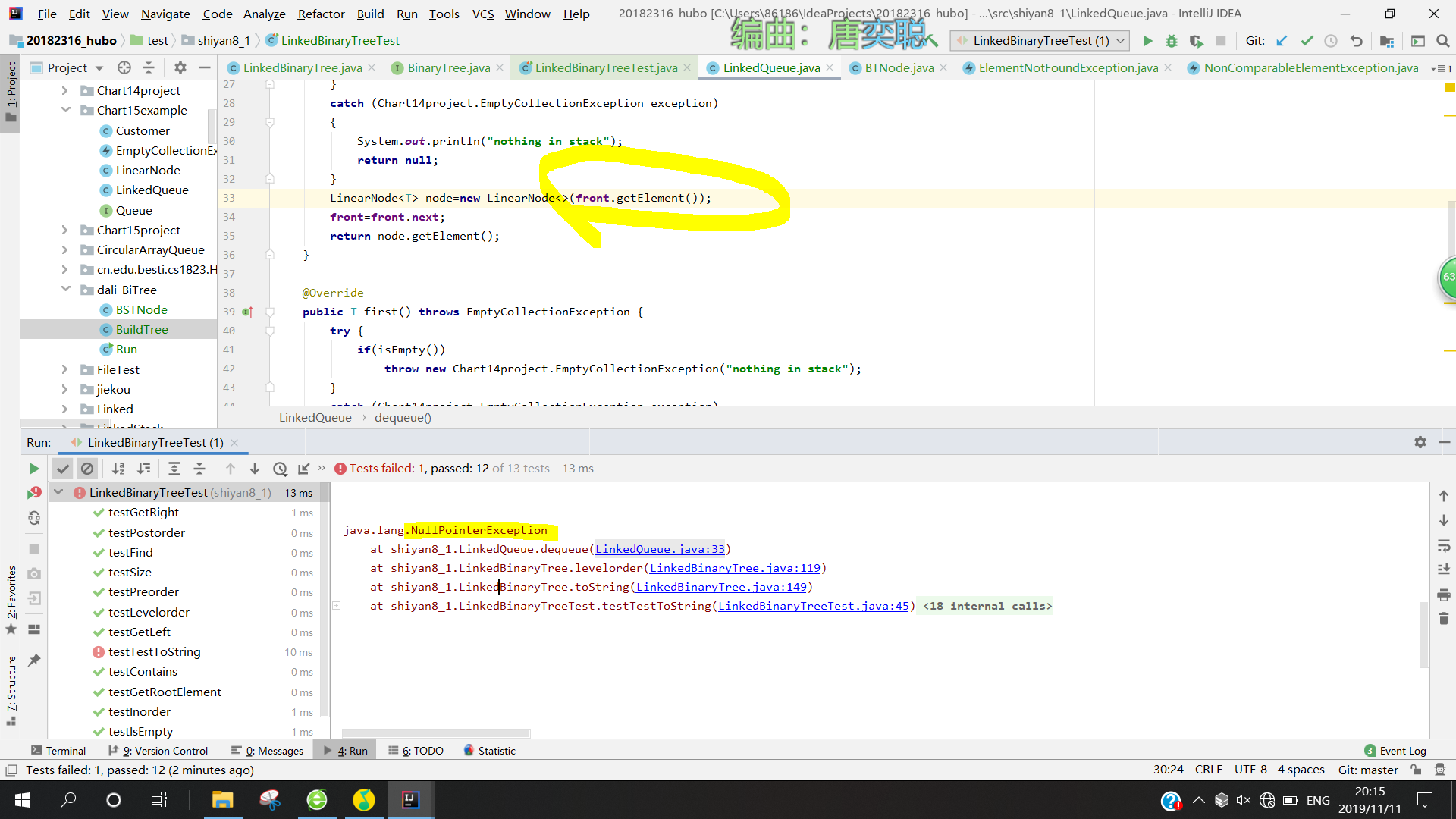
- 问题2解决方案:在之前代码中,我进行了一次队列元素增加,理论上front应该向前移了一位,但是我的front还是之前的,于是我将front作为参数传到了方法里面。
感悟
- 这次学习的查找与排序的方法,虽然最后输出的结果都是一样的,但是根据方法所占时间,需要的空间,以及稳定性等等有很多差别,虽然现在我们要处理的数据量很少,所以看不出什么差别,但是一旦数据量很大,差别就十分明显,所以要好好搞懂他们之间的差别。




